4.1. Вероятность попадания в мишень при одном выстреле равна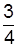 
и не зависит от порядкового номера выстрела. Найти вероятность того, что при 7 выстрелах произойдет: а) 5 попаданий в мишень; б) хотя бы одно попадание в мишень.
4.2. Монета подброшена 10 раз. Найти вероятность того, что герб выпадет: а) 4 раза; б) от 4 до 6 раз.
4.3. Среди выпускников военного училища в среднем 2% становятся генералами. Найти вероятность того, что из 100 выпускников одного года генералами станут: а) 3 человека; б) хотя бы один человек.
4.4. Найти вероятность того, что при пяти бросаниях игральной кости одно очко выпадет: а) 3 раза; б) от 2 до 4 раз.
4.5. В среднем в течение года преступники угоняют 1% зарегистрированных в городе автомобилей. Найти вероятность того, что из 300 автомобилей, принадлежащих сотрудникам организации, в течение года будет угнано: а) 2 автомобиля; б) не более 2 автомобилей.
4.6. Вероятность того, что станок в течение часа не потребует внимания рабочего, равна 0,6. Предполагая, что неполадки в станках независимы, найти вероятность того, что в течение часа внимания рабочего потребует: а) 2 из 5 обслуживаемых им станков; б) хотя бы один обслуживаемый им станок.
4.7. На автотранспортном предприятии каждый месяц нуждаются в ремонте в среднем 30% имеющихся автобусов. Найти вероятность того, что из 8 автобусов, обслуживающих данный маршрут, в течение месяца потребуют ремонта: а) 2 автобуса; б) менее 3 автобусов.
4.8. Доля изделий высшего сорта на данном предприятии составляет 20%. Найти вероятность того, что из пяти случайно отобранных изделий окажется: а) 2 изделия высшего сорта; б) не более 2 изделий высшего сорта.
4.9. Вероятность выигрыша крупной суммы по лотерейному билету равна 0,0025. Найти вероятность того, что из 800 человек, купивших по одному лотерейному билету, крупные суммы выиграют: а) ровно 2 человека; б) менее 3 человек.
4.10. Производится 6 независимых испытаний. При каждом испытании событие А появляется с одной и той же вероятностью 
. Найти вероятность того, что в данной серии испытаний событие А произойдет: а) 5 раз; б) не менее 5 раз.
4.11. Проверка качества выпускаемых деталей показала, что в среднем брак составляет 10%. Найти вероятность того, что в партии из 8 деталей окажется: а) 3 бракованных детали; б) 3 или 4 бракованных детали.
4.12. Применяемый метод лечения приводит к выздоровлению в 80% случаев. Найти вероятность того, что из пяти больных поправятся: а) 4 человека; б) не менее четырех человек.
4.13. Вероятность того, что изготовленная деталь не пройдет технический контроль из-за допущенного при обработке брака, равна 0,004. Найти вероятность того, что из 500 выпущенных за смену деталей не пройдут контроль: а) 2 детали; б) более 2 деталей.
4.14. Подбрасывается 5 монет. Найти вероятность того, что: а) выпадет 4 герба; б) выпадет более трех гербов.
4.15. На предприятии 90% сотрудников имеют высшее образование. Найти вероятность того, что из 6 случайно отобранных по списку сотрудников высшее образование имеют: а) 5 человек; б) 4 или 5 человек.
4.16. В среднем 2,5% мониторов персональных компьютеров выходят из строя до истечения гарантийного срока. Найти вероятность того, что из 160 купленных мониторов до истечения гарантийного срока сломаются: а) 3 монитора; б) менее 2 мониторов.
4.17. Вероятность того, что покупатель сделает покупку на сумму свыше 10000 рублей, равна 0,4. Найти вероятность того, что из 7 покупателей такую покупку сделают: а) 3 человека; б) хотя бы один человек.
4.18. Среди студентов математического факультета 70% получают стипендию. Найти вероятность того, что среди 6 случайно отобранных по списку студентов не получают стипендию: а) 2 человека; б) от 2 до 4 человек.
4.19. Вероятность получения высшего балла за ЕГЭ по математике равна 0,002. Найти вероятность того, что из 1500 старшеклассников города, которым предстоит сдавать экзамен, высший баллов получат: а) 4 ученика; б) хотя бы один ученик.
4.20. Найти вероятность того, что при семи бросаниях игральной менее 3 очков выпадет: а) 4 раза; б) хотя бы один раз.
4.21. Нарушения техники пожарной безопасности фиксируются, в среднем, в 40% организаций. Случайным образом для проверки выбирается 8 организаций. Найти вероятность того, что нарушения будут зафиксированы: а) в 3 организациях; б) в 2 или 3 организациях.
4.22. Вероятность попадания в мишень при одном выстреле равна 0,7 и не зависит от порядкового номера выстрела. Найти вероятность того, что при 5 выстрелах произойдет: а) 3 попадания в мишень; б) больше двух попаданий в мишень.
4.23. Вероятность того, что секретарь допустит орфографическую ошибку в слове, равна 0,004. Найти вероятность того, что в тексте из 750 слов будет допущено: а) 4 ошибки; б) от 3 до 5 ошибок.
4.24. По статистике каждый третий год в данной местности бывает неурожайным. Найти вероятность того, что из следующих 7 лет будет: а) 5 урожайных лет; б) не менее 5 урожайных лет.
4.25. Вероятность неправильного заполнения налоговой декларации консультантом по налогообложению равна 0,005. Найти вероятность того, что из 800 заполняемых им в течение квартала деклараций неправильно будут заполнены: а) 5 деклараций; б) не более одной декларации.
