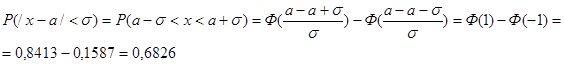Задача 2. Задана плотность распределения: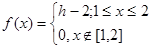 
Найти h.
Решение.
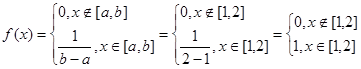
h-2=1 Þ h=3
Нормальное распределение. Случайная величина х называется нормально распределённой, если её плотность распределения f(x) имеет вид:
,
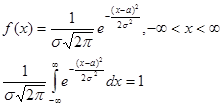где а и σ – параметры нормального распределения, σ >0.
В этом случае говорят, что х распределено нормально согласно закону N(a, σ).
Если а=0 и σ=1, то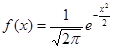 
и эта функция обозначается через φ(х) и называется плотностью нормированного и центрированного нормального распределения. Функция распределения в этом случае обозначается через 
.
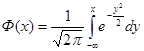Значения Ф(х) затабулированы, 
.
Задача 1. Рост мужчины в Москве имеет нормальное распределение. Средний рост мужчины в Москве а=175 см, σ=10 см. Какова вероятность, что рост первого встречного мужчины будет в пределах 160-190 см?
Решение.
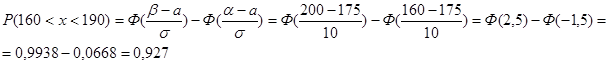
Правило трёх сигм. Случайная величина х распределена нормально N(a, σ).
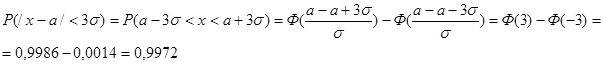
Задача 1. Рост мужчины в Москве имеет нормальное распределение. Средний рост мужчины в Москве а=175 см, σ=10 см. Какова вероятность, что рост первого встречного мужчины будет в пределах 145-205 см?
Решение.
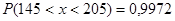
Правило двух сигм. Случайная величина х распределена нормально N(a, σ).
Правило одной сигмы. Случайная величина х распределена нормально N(a, σ).
