Пусть событие А заключается в том, что первый вытащенный билет оказался для студента «плохим», а В – второй – «хорошим». Поскольку после наступления события А один из «плохих» уже извлечён, то остаётся всего 29 билетов, из которых 25 студент знает. Отсюда искомая вероятность равна Р(В/А)=25/29.
Вероятность произведения:
p(AB)=p(A)*p(B|A)=p(B)*p(A|B).
Задача 1. По условиям предыдущего примера найти вероятность успешной сдачи экзамена, если для этого студент должен ответить на первый билет, или, не ответив на первый, обязательно ответить на второй.
Решение. Пусть события А и В заключаются в том, что соответственно первый и второй билеты «хорошие». Тогда  - появление «плохого» билета в первый раз. Экзамен будет сдан, если произойдёт событие А, или одновременно
- появление «плохого» билета в первый раз. Экзамен будет сдан, если произойдёт событие А, или одновременно  и В. То есть искомое событие С – успешная сдача экзамена выражается следующим образом: С=А+
и В. То есть искомое событие С – успешная сдача экзамена выражается следующим образом: С=А+  В. Отсюда
В. Отсюда
р(С)=р(А+  В)=р(А)+р(
В)=р(А)+р( В)=р(А)+р(
В)=р(А)+р( )р(В/
)р(В/  )=25/30+5/30*25/29=0,977
)=25/30+5/30*25/29=0,977
или
р(С)=1 - р( )=1 - р(
)=1 - р( *
* 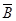 )=1 - р(
)=1 - р( )* р(
)* р( /
/ 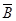 )=1 -5/30*4/29=0,977
)=1 -5/30*4/29=0,977
Случайные события А и В назовём независимыми, если
р(АВ)=р(А)*р(В).
Задача 2. Рассмотрим предыдущий пример сурной, содержащей N шаров, из которых n белых, но изменим опыт: вынув шар, мы кладём его обратно и только затем вынимаем следующий. А – событие, состоящее в том, что первым вынули белый шар, В – событие, состоящее в том, что первым вынули чёрный шар, а С – событие, состоящее в том, что вторым вынули белый шар; тогда
 ;
;  ;
;  ;
;  ;
;  ;
;
т.е. в этом случае события А и С независимы.






