Пусть мы имеем некое упорядоченное множество N состоящее из n различных элементов. Сочетанием из n элементов по k будет называться подмножество из k неповторяющихся элементов, выбранных из множества, состоящего из n элементов. Подмножества, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений. Обычно сочетание обозначается как Сnk и рассчитывается по формуле:
| Сnk = | n! k!(n - k)! |
Задача 1. Восемь студентов обменялись рукопожатиями. Сколько было рукопожатий?
Решение. В рукопожатии участвует «подмножество», состоящее из двух студентов (m=2), тогда как всё множество» студентов составляет 8 человек (n=8). Так как в процессе рукопожатия порядок не важен, выбираем формулу для числа сочетаний:
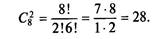
Задача. Сколькими способами можно составить трехцветный полосатый флаг из пяти различных по цвету отрезков материи?
Решение. Порядок важен, так как перестановка материи внутри трехцветного флга обозначает разные страны. Поэтому выбираем формулу числа размещений без повторений, где множество отрезков материи n = 5, а подмножество цветов m=3:

Задача 2. Сколько словарей надо издать, чтобы можно было выполнять переводы с любого из шести языков на любой из них?
Решение. Множество включает 6 языков n=6. Поскольку перевод есть отношение между двумя языками, то m=2, причем порядок важен, так как, например, словари русско-английский и англо-русский имеют различное применение. Поэтому выбираем размещения без повторений:

Задача 3. Сколько имеется вариантов составления расписания на понедельник, если предметов у студентов 9, а в понедельник 4 пары занятий, и предметы не повторяются?
Решение. а) Для студентов порядок не важен, поэтому выбираем формулу числа сочетаний:

б) Для преподавателей порядок важен, поэтому выбираем формулу размещений без повторений:

Задача 4. Сколькими способами можно расставить на книжной полке девять книг, среди которых есть трехтомник А.С. Пушкина?
Решение.
Так как три тома, входящие в трехтомник, должны стоять рядом, причем по возрастанию номера славе направо, то рассматриваем их как один элемент данного множества, в котором имеется еще 6 элементов. Поэтому выбираем перестановки без повторений во множестве, содержащем семь элементов:
Р7 = 7! = 5040
Задача 5. Сколькими способами можно назначить в группе из 30 человек трех дежурных?
Решение.
а) Если их роль в процессе дежурства одинакова, то порядок не важен, поэтому выбираем сочетания без повторений:
С 330 = 30! / 3!27! = 4060
б) Если порядок важен, т.е. во время дежурства их функциональные обязанности различны, то по формуле размещения без повторений имеем:
А 330 = 30! / 27! = 24360
Задача 6. Сколько существует шестизначных телефонных номеров, у которых: а) возможны любые цифры; б) все цифры различные?
Решение.
а) 1. Так как в шестизначном наборе телефонного номера возможны любые цифры, то на каждом из шести мест может встретиться любая из 10-ти цифр от 0 до 9. Необходимо из всех возможных десяти цифр выбрать лишь те шесть, которые будут испльзованы для для шастизначных телефонных номеров. Поскольку в записи телефонных номеров порядок расположения цифр важен, по формуле размещений с повторениями имеем:
А 106 = 106 = 1000000
2. Как известно, не бывает шестизначных номеров, начинающихся с нуля, поэтому надо подсчитать их количество и вычесть его из общего числа комбинаций. Число номеров, первая цифра у которых 0, найдем по формуле размещений с повторениями, «зафиксировав» ноль т.е. на каждом из пяти остальных возможных мест может встретиться любая из десяти цифр от
0 до 9. Тогда число таких комбинаций:
А105 = 105 = 100000
3. Общее число шестизначных телефонных номеров, у которых могут быть любые, в том числе и повторяющиеся, цифры, равно разности:
А106 – А 105 = 106 – 105 = 1000000 – 100000 = 900000
б) 1. Пусть теперь в шестизначном наборе все цифры различные. Необходимо из всех возможных десяти цифр выбрать лишь те шесть, которые используются для шестизначных телефонных номеров, причем никакая цифра не повторяется. Тогда по формуле размещений без повторений имеем:
А 106 = 10! / (10 – 6)! = 5х6х7х8х9х10 = 151200
2. Поскольку шестизначных номеров, начинающихся с нуля, не бывает, надо посчитать их количество и вычесть его из общего числа комбинаций. Число номеров, первая цифра у которых 0, найдем по формуле размещений без повторений, «зафиксировав ноль», т.е. на каждом из пяти оставшихся возможных мест могут встретиться цифры от 0 до 9. Тогда число таких комбинаций найдем по формуле размещений без повторений. Имеем:
А 105 = 10! / (10-5)! = 6х7х8х9х10 = 30240
3. Общее число шестизначных телефонных номеров, у которых не может быть повторяющихся цифр, равно разности:
А106 – А 105 = 106 – 105 = 151200 – 30240 = 120960
Задача 7. Сколькими способами можно выделить делегацию в составе трех человек, выбирая их среди четырех супружеских пар, если:
а) в состав делегации входят любые трое из данных восьми человек;
б) делегация должна состоять из двух женщин и одного мужчины;
в делегацию не входят члены одной семьи?
Решение.
а) Порядок не важен:
С 83 = 8! / 3! 5! = 56
б) Выберем двух женщин из имеющихся 4-х С42 способами и одного мужчину из 4-х С 41 способами. По правилу произведения (и мужчина, и две женщины) имеем С42 х С41 = 24.
в) Из четырех семей выбираем 3-х членов делегации четырьмя способами (т.к. С 43 = 4! / 3!1! = 4). Но в каждой семье имеется по два способа выбора члена делегации. По правилу произведения С43 х2х2х2 = 4х8 =32.
Задача 8. В колледже учится 2000 студентов. Можно ли утверждать, что хотя бы двое из них имеют одинаковые инициалы и имени, и фамилии?
Решение.
В русском алфавите 33 буквы, из них ъ, ь, ы, й не могут быть использованы, поэтому n = 33-4 = 29. Каждая из 29 букв может быть инициалом и имени, и фамилии. По правилу произведения 29х29 = 841 < 2000. Значит может быть лишь 841 различных вариантов, и среди 2000 студентов обязательно будут совпадения.






