Понятие интеграла может быть расширено на функции двух и большего числа переменных. Рассмотрим, например, функцию двух переменных z = f (x,y). Двойной интеграл от функции f (x,y) обозначается как
где R - область интегрирования в плоскости O xy. Если определенный интеграл 
от функции одной переменной 
выражает площадь под кривой f (x) в интервале от x = a до x = b, то двойной интеграл выражает объем под поверхностью z = f (x,y) выше плоскости O xy в области интегрирования R
Свойства двойного интеграла
Двойной интеграл обладает следующими свойствами:
1. 
2. 
3. 
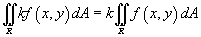, где k - константа;
4. Если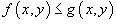 
в области R, то 
;
5. Если 
в области R и 
(рисунок 4), то 
;
6. Если на R и области R и S являются непересекающимися (рисунок 5), то 
.
Здесь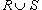 
означает объединение этих двух областей.
29) Сведение двойного интеграла к повторному
