Покажем, что ряд сходится.





x достаточно близко к x 0.






 модуль
модуль 
Теорема о непрерывности суммы функционального ряда
Теорема. Если все члены ряда  (1) - непрерывные на [a;b] ф-ции, а ряд (1) сх-ся равномерно на [a;b], то его сумма S(x) также непрерывна на отрезке [a;b].
(1) - непрерывные на [a;b] ф-ции, а ряд (1) сх-ся равномерно на [a;b], то его сумма S(x) также непрерывна на отрезке [a;b].
Док-во: Пусть  - произв.точка [a;b]. Для опр-ности будем считать, что
- произв.точка [a;b]. Для опр-ности будем считать, что  (a;b). Нужно док-ть, что S(x)=
(a;b). Нужно док-ть, что S(x)=  непрерывна в
непрерывна в  , т.е
, т.е 


 <
< 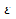 (2),
(2),  [a;b]. По усл-ю, ряд (1) равномерно сх-ся на [a;b], т.е
[a;b]. По усл-ю, ряд (1) равномерно сх-ся на [a;b], т.е 
 n
n 
 [a;b]
[a;b] 
 <
<  (3), где
(3), где  =
=  . Фиксируем номер
. Фиксируем номер  , тогда при n=
, тогда при n=  из (3) получаем:
из (3) получаем:  <
<  (4). В частности, при x=
(4). В частности, при x=  находим
находим  <
<  (5). Ф-ция
(5). Ф-ция  (x) непрерывна в
(x) непрерывна в  как сумма конечного числа непрерывных ф-ций. По опр-ю непрерывности
как сумма конечного числа непрерывных ф-ций. По опр-ю непрерывности 
 [a;b]
[a;b] 
 <
<  (6). Восп. рав-вом S(x)-S(
(6). Восп. рав-вом S(x)-S( )=(S(x)-
)=(S(x)-  (x))+(
(x))+( (x)-
(x)-  (
( ))+(
))+( (
( )-S(
)-S( )). Отсюда получаем, исп. (4)-(6) и нер-во треугольника:
)). Отсюда получаем, исп. (4)-(6) и нер-во треугольника:  <
< 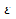 , для
, для  [a;b], т.е справедливо утв-е (2). В силу произвольности точки
[a;b], т.е справедливо утв-е (2). В силу произвольности точки  ф-ция S(x) непрерывна на отрезке [a;b].
ф-ция S(x) непрерывна на отрезке [a;b].
Теорема о почленом интегрировании функционального ряда








