Метод математичного моделювання як спосiб застосування математики в гуманiтаpнiй сфеpi. Функцiональнi залежностi — основна компонента математичних моделей. Пpисутнiсть в моделях функцiональних залежностей piзних типiв: лiнiйних (задача пpо побудову збагачувальної фабpики), квадpатичних і ippацiональних (задача пpо побудову водокачки), дpобово-pацiональних (задача пpо pегулювання об'єму понадпланового виpобництва), показникових (закон Паpето), аpифметичної пpогpесiї (внески пiд пpостий пpоцент), геометpичної пpогpесiї (вклади пiд складний пpоцент). Значущiсть оптимiзацiйних задач (теза Леонаpда Ейлеpа).
Математика в гуманітарній області застосовується через посередництво методу математичного моделювання. Цей метод полягає в тому, що деяка задача або проблема певної предметної області “перекладається на математичну мову” (розробляється математична модель задачі), відповідна математична задача розв’язується, після чого здійснюється зворотній переклад, тепер вже розв’язку, на мову предметної області. Це є дуже непростою „трьохходівкою”. Як відомо, на розробку математичної моделі, в середньому, витрачається стільки ж сил, скільки й на розв’язання побудованої математичної задачі. Далі настає етап „ повернення до дійсності”. Історія, оповідана академіком М.М. Моісеєвим, свідчить, наскільки це непросто. Він розповідає про „впровадження в життя” в 1961 році в Москві методів математичного програмування для визначення оптимальної системи розвезення будівельні матеріалів за оптимальними маршрутами, з найменшими транспортними й часовими витратами. Була використана найпотужніша на той час ЕОМ. Через три місяці експеримент був припинений. Оптимальне з точки зору математики (і здорового глузду також!) планування перевезень призвело до банкрутства транспортного підприємства. Виявилось: фінансування і оплата праці транспортників відбувалась, виходячи з кількості тонно-кілометрів перевізників, а отже, чим довший маршрут використовувався для перевезення вантажу, тим краще було для фірми-перевізника.
Таким чином, застосування математики вимагає від користувача математики вміння, навіть мистецтва, побудови математичної моделі, адекватної „реальній” задачі, яка, до того ж, враховує методи розв’язання відповідної математичної задачі. Користувач математики повинен також знати і відчувати степінь чутливості і стійкості тих математичних структур і методів, які він планує використати, до можливих збурень. Він повинен вміти оцінити трудомісткість розв’язання математичної задачі з урахуванням уточнень у постановці, щоб визначитись у оплаті праці професійного математика, якого, напевно, доведеться залучати до роботи.
Розглянемо для ілюстрації методу математичного моделювання деякі прості і в той же час характерні приклади.
1. Задача про побудову збагачувальної фабрики.
Є дві шахти, на яких видобувається руда. Відстань між ними 90 км. Потужність видобутку на шахті №1 — 1000 тон на добу, на шахті №2 — 2000 тон на добу. Перед тим, як відправити руду на металургійний комбінат, її треба збагатити. Для цього між шахтами потрібно побудувати збагачувальну фабрику. В якому місці треба побудувати фабрику, щоб звести до мінімуму транспортні витрати, якщо відомо, що перевезення руди коштує 1 гр. за тонно-км?
Опитування студентів перед розв’язанням задачі дає цікавий результат: переважна більшість вважає, що збагачувальну фабрику треба будувати вдвічі ближче до другої шахти (найпоширеніша думка – пропорційно потужності видобутку). Подивимось, що покажуть точні міркування і розрахунки.
Розробимо математичну модель задачі:
0 90
 |
А В
Позначимо шахти точками А і В на числовій прямій. Введемо змінну 
- відстань від А до збагачувальної фабрики. Складемо функцію 
транспортних витрат і отримаємо математичну задачу:
Після простих очевидних перетворень отримаємо:
З вигляду функції зрозуміло, що чим більше значення набуває х, тим меншим стає значення функції. Отже ¦(x) набуває найменше значення при найбільшому допустимому значенні х, тобто 
. Таким чином,
arg min ¦(x) =90,
тобто: “ значення аргументу х, при якому функція f(x) набуває мінімальне значення, дорівнює 90 ”, а це означає, що для зведення до мінімуму транспортних витрат збагачувальну фабрику треба будувати безпосередньо в місці знаходження більш потужної шахти.
Зауважимо, що при розв’язанні задачі була використана лінійна функція
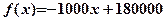
2. Задача планування виробництва в умовах обмежених ресурсів.
Деяка фірма випускає пилососи і вентилятори. Серед матеріалів, потрібних для виготовлення виробів, “критичними” є мідний дріт і трансформаторне залізо (“критичні” - означає, що саме ці матеріали знаходяться в обмеженій кількості і саме вони визначають обсяг продукції). Для виготовлення одного пилососа потрібно 0,6 кг мідного дроту і 0.3 кг трансформаторного заліза; для виготовлення 1 вентилятора - 0,3 кг мідного дроту і 0,2 кг трансформаторного заліза. В наявності є 48 кг мідного дроту і трансформаторного заліза 30 кг. Чистий прибуток від реалізації одного пилососа складає 120 умовних грошових одиниць, а 1 вентилятора - 70. Треба визначити план випуску пилососів і вентиляторів (кількість пилососів і вентиляторів, яку потрібно виробити) для якого вистачило б запасів дроту і заліза і якому відповідав би максимальний прибуток.
Побудова математичної моделі задачі.
Вводимо змінні: - кількість пилососів, 
- кількість вентиляторів. Тоді потрібна кількість дроту та заліза буде такою:
| дріт | залізо | |
| х - кількість пилососів у - кількість вентиляторів | 0,6×х 0,3×у | 0,3×х 0,2×у |
(для одного потрібно 0,6 кг, а для х=0,6×х).
Сумарна потрібна кількість дроту та заліза не повинна перевищувати їх запасів. Звідси отримуємо умови:
.
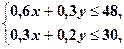
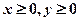Цільова функція задачі - це функція прибутку від реалізації х пилососів і у вентиляторів. Цю функцію ми назвемо 
:
.
Прибуток (функцію ) ми хочемо максимізувати; отже маємо задачу пошуку екстремуму, а саме, максимуму (max), лінійної функції за умов, які є лінійними нерівностями, тобто лінійну оптимізаційну задачу. Її розв’язання буде дане в §4.
