Метод координат.............................................................................24
Декартова система координат. Координати точки.......................24
1.2. Відстань між двома точками. Рівняння кола та сфери................26
1.3. Ділення відрізка у даному відношенні............................................28
1.4. Пряма лінія на площині.....................................................................30
1.5. Площина в просторі............................................................................34
1.6. Пряма лінія в просторі.......................................................................34
1.7. „За числами бачити фігури”.............................................................35
§2. Перетин прямих ліній і площин..................................................37
2.1. Знаходження точки перетину двох прямих ліній на площині...37
2.2. Знаходження точки перетину трьох площин у просторі.............40
2.3. Перетин двох прямих на площині; одна з прямих
задана канонічним рівнянням.................................................................45
2.4. Знаходження точки перетину прямої і площини..........................46
§3. Вступ до векторної алгебри..........................................................47
3.1. Поняття вільного вектора.................................................................47
3.2. Арифметичні операції над векторами.............................................50
3.2.1. Множення вектора на число............................................................. 50
3.2.2. Сума двох векторів............................................................................. 50
3.2.3. Різниця двох векторів........................................................................ 52
3.2.4. Поняття лінійної комбінації векторів.............................................
3.3. Координатне подання арифметичних операцій над векторами 53
Поняття одиничного декартового базису. Розкладення
векторів за базисом....................................................................................54
3.5. Скалярний добуток векторів, його обчислення і застосування.55
3.5.1. Означення і властивості скалярного добутку................................ 55
3.5.2. Застосування скалярного добутку................................................... 56
3.6. Точки та їх радіус-вектори................................................................59
§4. Розв’язання задач лінійного програмування малої
розмірності засобами аналітичної геометрії............................62
4.1. Математична модель задачі лінійного програмування................62
4.1.1. Задача планування виробництва в умовах обмежених ресурсів..... 62
4.1.2. Формалізація задачі планування виробництва в умовах
обмежених ресурсів...................................................................................... 62
4.1.3. Загальна структура задачі лінійного програмування..................... 63
4.2. Розв’язання ЗЛП...................................................................................63
4.2.1. Побудова допустимої області ЗЛП.................................................. 63
4 .2.2. Пошук оптимального допустимого розв’язку................................. 65
4 .3. Загальні властивості оптимального розв’язку ЗЛП..................... 66
4.3.1. Основна властивість оптимального розв’язку ЗЛП....................... 66
4 .3.2. Знаходження оптимального розв’язку ЗЛП методом
перебирання вершин допустимої області.................................................. 67
4.3.3. Класифікація можливостей щодо “вмісту”множини
оптимальних розв’язків ЗЛП....................................................................... 67
§5. Векторний добуток векторів, його обчислення
та застосування......................................................................................69
Поняття векторного добутку..............................................................69
5.2. Властивості векторного добутку........................................................70
Координатне подання векторного добутку......................................71
Координатне подання векторного добутку в
детермінантній формі..................................................................................73
5.5. Контрольна перевірка правильності обчислення
векторного добутку......................................................................................74
Застосування векторного добутку.....................................................74
§6. Змішаний добуток векторів, його обчислення та
застосування.........................................................................................76
6.1. Поняття змішаного добутку................................................................76
6.2. Властивості змішаного добутку.........................................................76
6.2.1. Геометричний зміст змішаного добутку......................................... 76
6.2.2. Критерій компланарності векторів і точок.................................... 77
6.2.3. Алгебраїчні властивості змішаного добутку................................... 77
6.3. Координатне подання змішаного добутку.......................................78
6.4. Застосування змішаного добутку.......................................................79
§7. Метричні характеристики і взаємне розташування
геометричних об’єктів.........................................................................82
7.1. Точки і прямі лінії на площині..........................................................82
7.1.1. Відстань між двома точками.......................................................... 82
7.1.2. Відстань від точки до прямої........................................................... 82
7.1.3. Відстань між двома паралельними прямими.................................. 83
7.1.4. Взаємне розташування точок відносно прямої............................... 83
7.2. Точки і площини в просторі...............................................................84
7.3. Точки і прямі в просторі.....................................................................84
7.4. Пряма і площина в просторі..............................................................85
7.5. Площі......................................................................................................85
7.6. Об’єми.....................................................................................................86
7.7. Дві прямі в просторі.............................................................................86
7.7.1. Паралельність прямих......................................................................... 86
7.7.2. Умова перетину просторових прямих............................................... 86
7.7.3. Знаходження пари найближчих точок на мимобіжних прями.х... 87
Розділ ІІ. ЛІНІЙНА АЛГЕБРА...........................................................92
§8. Системи лінійних рівнянь і n -вимірні вектори........................93
8.1. Поняття системи лінійних рівнянь, системи лінійних
нерівностей та їх розв’язків.............................................................92
8.2. Поняття n -вимірного вектора і n -вимірного лінійного
векторного простору.........................................................................95
8.3. Загальні теореми про множину розв’язків систем лінійних
рівнянь................................................................................................96
Теорема Крамера для квадратних СЛР..................................99
§9. Лінійні векторні простори...........................................................102
9.1. Загальне поняття лінійного векторного простору......................102
9.2. Підпростори лінійних векторних просторів................................104
9.3. Геометрія лінійних векторних просторів.....................................105
9.4. Опуклі множини в п -вимірному просторі.....................................110
§10. Метод Гауса розв’язання систем лінійних рівнянь..............115
10.1. Загальна ідея методу Гауса....................................................115
10.2. Поняття загального розв’язку СЛР......................................117
10.3. Елементарні перетворення СЛР..........................................119
Перетворення виключення...................................................120
10.5. Умова несумісності СЛР.........................................................120
10.6. Вилучення залежних рівнянь................................................120
Алгоритм методу Гауса...........................................................121
Матрична форма методу Гауса..............................................121
§11. Елементи матричної алгебри....................................................122
11.1. Вступ до матричної алгебри...........................................................122
11.2. Арифметичні операції над матрицями........................................124
11.2.1. Множення матриці на число........................................................ 124
11.2.2. Додавання та віднімання матриць............................................... 124
11.2.3. Множення матриці на матрицю.................................................. 125
11.3. Економічне тлумачення операції матричного
множення....................................................................................................126
11.4. Властивості операцій над матрицями..........................................127
11.4.1. Асоціативність операції матричного множення....................... 127
11.4.2. Некомутативність операції матричного множення................ 127
11.4.3. Адитивність по першому і другому множнику операції
матричного множення.............................................................................. 127
11.4.4. Існування та єдиність нейтрального елемента відносно
операції матричного множення.............................................................. 127
11.4.5. Анулююча властивість нульової матриці.................................... 128
11.5. Мультиплікативна форма методу Гауса......................................129
11.6.Обернена матриця, її обчислення і застосування........................129
11.6.1. Поняття оберненої матриці......................................................... 129
11.6.2. Формула для обчислення оберненої матриці............................... 130
11.6.3. Обчислення оберненої матриці методом Гауса.......................... 130
11.7. Застосування оберненої матриці до розв’язання систем
лінійних рівнянь........................................................................................133
§12. Визначники n -го порядку, їх обчислення та
застосування...............................................................................135
12.1. Аналіз спільних властивостей визначників 2-го та 3-го
порядку....................................................................................................... 135
Поняття визначника n-го порядку................................................137
12.3. Обчислення визначників n-го порядку за означенням.............138
12.4. Метод Гауса обчислення визначників..........................................139
Розкладення визначника за елементами рядка (або
стовпчика)...................................................................................................140
12.6. Детермінантна формула для оберненої матриці.........................142
12.7. Властивості визначників.................................................................142
Теорема Крамера (загальний випадок)........................................144
12.9. Інтерполяційний многочлен...........................................................144
§13. Лінійна залежність і незалежність n-вимірних
векторів........................................................................................147
13.1. На підходах до поняття лінійної залежності і незалежності.... 147
13.1.1.Колінеарність векторів................................................................... 147
13.1.2. Компланарність векторів.............................................................. 148
13.1.3. Знаходження методом Гаусса рівнянь-наслідків........................ 148
13.1.4. Векторний погляд на систему лінійних рівнянь........................... 149
13.2. Загальне поняття лінійної залежності і незалежності...............150
13.3. Лінійна залежність в ℝ2 і ℝ3...........................................................151
13.4. Властивості лінійно залежних і лінійно незалежних систем
n -вимірних векторів..................................................................................152
13.5. Базиси n -вимірних векторних просторів.....................................154
13.6. Фундаментальна система розв’язків системи лінійних
рівнянь.........................................................................................................159
13.7. Критерій сумісності систем лінійних рівнянь.............................161
Розділ ІІІ. МАТЕМАТИЧНИЙ АНАЛІЗ.........................................163
§ 14. Числа і числові множини..........................................................164
14.1. Основні види чисел..........................................................................164
14.2. Ірраціональність числа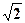 
.............................................................164
14.3. Числова вісь та числові інтервали................................................166
Теореми Георга Кантора.................................................................169
Алгебра множин................................................................................172
§ 15. Функції..........................................................................................175
15.1. Поняття функції................................................................................175
15.2. Дослідження функцій.......................................................................176
15.3. Поняття графіку функції.................................................................176
15.4. Основні характеристики функцій.................................................177
Збiжнiсть i гpаницi числових послiдовностей.......................185
16.1. Поняття числової послідовності....................................................185
16.2. Поняття збіжності і границі числової послідовності.................187
16.3. Властивостi опеpацiї гpаничного пеpеходу..................................188
16.4. Чудові (особливі) границі................................................................191
16.4.1. Число 
............................................................................................. 192
16.4.2. Число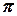 
............................................................................................ 192
16.4.3.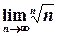 
............................................................................................... 194
16.4.4. 
............................................................................................... 194
16.4.5.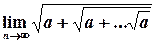 
......................................................................... 194
16.5. Уточнення і обґрунтування деяких математичних
понять......................................................................................................... 194
16.5.1. Поняття дійсного числа................................................................ 194
16.5.2. Степінь з ірраціональним показником.......................................... 195
§ 17. Збiжнiсть i гpаницi функцій. Неперервні і розривні
функції...................................................................................................196
17.1. Асимптотична поведінка функції................................................. 196
17.2. Поняття границі функції................................................................ 198
17.3. Поняття асимптоти функції........................................................... 199
17.4. Неперервні функції...........................................................................200
17.4.1. Поняття неперервності функції................................................... 200
17.4.2. Найпростіші властивості неперервних функцій......................... 200
17.4.3. Головні властивості неперервних функцій................................... 201
17.4.4. Функціональні рівняння Коші......................................................... 203
Многочлени....................................................................................... 203
17.5.1. Поняття многочлена...................................................................... 203
17.5.2. Поліном 3-го степеня..................................................................... 204
17.5.3. Раціональні функції......................................................................... 205
17.5.4. Локалізація дійсних коренів многочлена....................................... 206
Похiдна..........................................................................................207
Теорема Ферма................................................................................. 207
18.2. Поняття похідної.............................................................................. 209
18.3. Знаходження і аналіз точок екстремумів функцій.................... 212
18.4. Найпростіші властивості похідної (похідна суми, різниці,
добутку, частки функцій)........................................................................ 214
18.5. Похідна складеної функції. Ланцюгове правило....................... 214
18.6. Похідна оберненої функції.............................................................. 215
18.7. Логарифмічна похідна.................................................................... 217
18.8. Основні теореми диференціального числення........................... 217
18.9. Диференціал функції....................................................................... 218
18.10. Прикладні задачі на екстремум.................................................. 221
18.11. Таблиця похідних........................................................................... 222
Iнтегpал........................................................................................ 223
Метод вичерпування....................................................................... 223
19.2. Деякі показові задачі........................................................................225
19.2.1. Задача про середню швидкість..................................................... 225
19.2.2. Задача про пройдений шлях........................................................... 226
19.3. Поняття визначеного інтегралу.................................................... 227
19.4. Існування і властивості визначеного інтегралу........................ 231
19.5. Напіввизначений-напівневизначений інтеграл (інтеграл
зі змінною верхньою межею)................................................................. 231
19.6. Первісна функція і невизначений інтеграл............................... 233
19.7. Формула Ньютона-Лейбніца 
основна теорема
диференціального та інтегрального числення.................................... 234
19.8. Властивості невизначеного інтегралу......................................... 237
19.9. Способи обчислення невизначених інтегралів.......................... 237
19.9.1. Загальна ситуація щодо обчислення інтегралів.......................... 237
19.9.2. Головне правило інтегрування....................................................... 238
19.9.3.Використання найпростіших правил інтегрування і таблиці інтегралів..................................................................................................... 238
19.9.4.Метод заміни змінних (інтегрування підстановкою).................. 240
19.9.5. Метод інтегрування частинами................................................... 240
Дифеpенцiальнi piвняння......................................................... 241
20.1. Диференціальні рівняння як математичні моделі
динамічних процесів..................................................................................241
20.2. Загальне поняття диференціального рівняння..........................244
20.3. Диференціальні рівняння з відокремленими змінними...........247
20.4. Лінійні диференціальні рівняння..................................................249
§ 21. Функцiї багатьох змiнних......................................................... 252
21.1. Функції багатьох змінних в математичних моделях
прикладних задач.......................................................................................252
21.2. Загальне поняття функції багатьох змінних...............................255
21.3. Частинні похідні функції багатьох змінних. Узагальнена
теорема Ферма...........................................................................................258
21.4. Градієнт функції................................................................................262
ЗБІРНИК ЗАДАЧ І ВПРАВ................................................................269
ЛІТЕРАТУРА.......................................................................................293
ДОДАТКИ.............................................................................................295
