| ТРАЕКТОРИЯ | †линия, которую описывает материальная точка (или тело) при своем движении; По траектории различают два вида движения: поступательное и вращательное. | |||||||||||||||||||||||||||
| ПУТЬ ∆S [м] | † положительная скалярная величина, не убывающая со временем;
† расстояние ∆S, пройденное материальной точкой (телом) по её траектории;
† пути, пройденные точкой (телом) за последовательные промежутки времени, складываются арифметически;
† ∆S=  пройденный путь равен модулю перемещения при прямолинейном движении в одном направлении;
По характеру зависимости пути от времени движения делятся на равномерные и неравномерные. пройденный путь равен модулю перемещения при прямолинейном движении в одном направлении;
По характеру зависимости пути от времени движения делятся на равномерные и неравномерные.
| |||||||||||||||||||||||||||

 ∆S
∆S
| ||||||||||||||||||||||||||||
ПЕРЕМЕЩЕНИЕ  [м] [м]


| † направленный отрезок, проведенный из начальной точки М1 в заданную точку М2 траектории (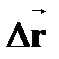 - вектор)
† векторы перемещений складываются
геометрически: если материальная точка (тело) одновременно участвует в нескольких движениях, то результирующее перемещение равно векторной сумме перемещений, совершаемых точкой (телом) в каждом из движений; - вектор)
† векторы перемещений складываются
геометрически: если материальная точка (тело) одновременно участвует в нескольких движениях, то результирующее перемещение равно векторной сумме перемещений, совершаемых точкой (телом) в каждом из движений;
| |||||||||||||||||||||||||||
| ПОСТУПАТЕЛЬНОЕ движение † движение, при котором любая прямая, проведенная в теле, остается параллельной самой себе; † траектории всех точек тела одинаковые; | ||||||||||||||||||||||||||||
| СКОРОСТЬ | † быстрота изменения перемещения со временем; † определяет направление тела в данный момент времени; † векторная физическая величина; | |||||||||||||||||||||||||||
Средняя скорость
 [м/с] [м/с]

| † отношение перемещения  к промежутку времени к промежутку времени  , в течение которого это перемещение произошло;
† вектор средней скорости , в течение которого это перемещение произошло;
† вектор средней скорости  совпадает с направлением вектора перемещения совпадает с направлением вектора перемещения  ; ;
| |||||||||||||||||||||||||||
— модуль
средней скорости
(средняя путевая скорость)
 = =  [м/с] [м/с]
| † отношение пройденного пути ΔS за промежуток времени Δt
 † скалярная величина;
† скалярная величина;
| |||||||||||||||||||||||||||
Мгновенная скорость
 [м/с] [м/с]
| † скорость в данный момент времени (в данной точке траектории);
† предел (Ɩim), к которому стремится средняя скорость 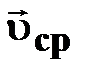 за бесконечно малый промежуток времени Δt за бесконечно малый промежуток времени Δt
 †
†  = = 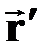 - первая производная перемещения по времени;
† вектор мгновенной скорости - первая производная перемещения по времени;
† вектор мгновенной скорости  направлен по касательной к траектории в сторону движения; направлен по касательной к траектории в сторону движения;
| |||||||||||||||||||||||||||
— модуль
мгновенной скорости
 [м/с] [м/с]
| † 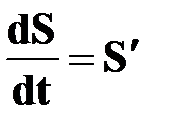 - первая производная пути по времени; - первая производная пути по времени;
 † скалярная величина;
† скалярная величина;
| |||||||||||||||||||||||||||
| УСКОРЕНИЕ | † характеристика неравномерного движения; † быстрота изменения скорости со временем; † векторная физическая величина; | |||||||||||||||||||||||||||
Среднее ускорение
 [м/с2] [м/с2]
| †  -изменение скорости за промежуток
времени -изменение скорости за промежуток
времени  ;
† векторная физическая величина; ;
† векторная физическая величина;
| |||||||||||||||||||||||||||
Мгновенное ускорение
 [м/с2] [м/с2]
| † ускорение в данный момент времени;
†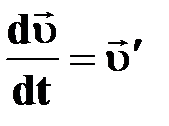 первая производная скорости по времени;
† предел (Ɩim), к которому стремится среднее ускорение первая производная скорости по времени;
† предел (Ɩim), к которому стремится среднее ускорение  за бесконечно малый промежуток времени Δt за бесконечно малый промежуток времени Δt

| |||||||||||||||||||||||||||
| СОСТАВЛЯЮЩИЕ УСКОРЕНИЯ | ||||||||||||||||||||||||||||
—тангенциальное
ускорение
 [м/с2] [м/с2]

| † характеризует быстроту изменения скорости по модулю;
†  направлено по касательной к траектории;
†т.к. направлено по касательной к траектории;
†т.к.  , ,  
| 
| ||||||||||||||||||||||||||
— нормальное
ускорение
 или или  [м/с2] [м/с2]
| † характеризуетбыстроту изменения скорости по направлению;
†  направлено к центру кривизны траектории радиусом R.
†т.к. направлено к центру кривизны траектории радиусом R.
†т.к.  , , 
| |||||||||||||||||||||||||||
Полное ускорение

| † геометрическая сумма тангенциальной  и нормальной
и нормальной  составляющих; составляющих;
| |||||||||||||||||||||||||||
— модуль
полного ускорения
 [м/с2] [м/с2]
|
†   ; ;
| |||||||||||||||||||||||||||
| ПРИМЕРЫ РАЗЛИЧНЫХ ВИДОВ ДВИЖЕНИЯ | ||||||||||||||||||||||||||||
| РАВНОМЕРНОЕ движение | † движение, при котором материальная точка (тело) за любые равные промежутки времени совершает одинаковые перемещения; | |||||||||||||||||||||||||||
| ПРЯМОЛИНЕЙНОЕ движение | † движение, при котором траектория материальной точки – прямая линия; | |||||||||||||||||||||||||||
РАВНОМЕРНОЕ
ПРЯМОЛИНЕЙНОЕ
движение
 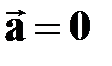
| † движение с постоянной по модулю и направлению скоростью;
† средняя скорость 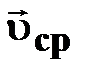 равна мгновенной скорости равна мгновенной скорости  ; ;
| |||||||||||||||||||||||||||
| ПУТЬ | † 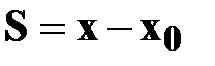
| х0, х –начальная и конечная координаты; | ||||||||||||||||||||||||||
ПЕРЕМЕЩЕНИЕ

| † 
| |||||||||||||||||||||||||||
†  - путь равен модулю вектора перемещения при движении точки по прямой линии в одном направлении; - путь равен модулю вектора перемещения при движении точки по прямой линии в одном направлении;
| ||||||||||||||||||||||||||||
Скорость средняя
 [м/с] [м/с]
| †  - перемещение точки за промежуток времени - перемещение точки за промежуток времени  ;
† направление ;
† направление  совпадает с направлением совпадает с направлением  ;
† векторная величина; ;
† векторная величина;
| |||||||||||||||||||||||||||
Модуль
средней скорости
 = =  [м/с] [м/с]
| ➨ отношение пройденного пути S к промежутку времени t, за который этот путь пройден; † скалярная величина; | |||||||||||||||||||||||||||
| Уравнение координаты | 
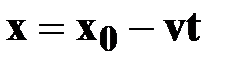
| ➨ - вектор скорости  и ось ОХсонаправлены;
➨ - вектор скорости и ось ОХсонаправлены;
➨ - вектор скорости  и ось ОХпротивоположны; и ось ОХпротивоположны;
| ||||||||||||||||||||||||||
| Графическое представление равномерного прямолинейного движения | 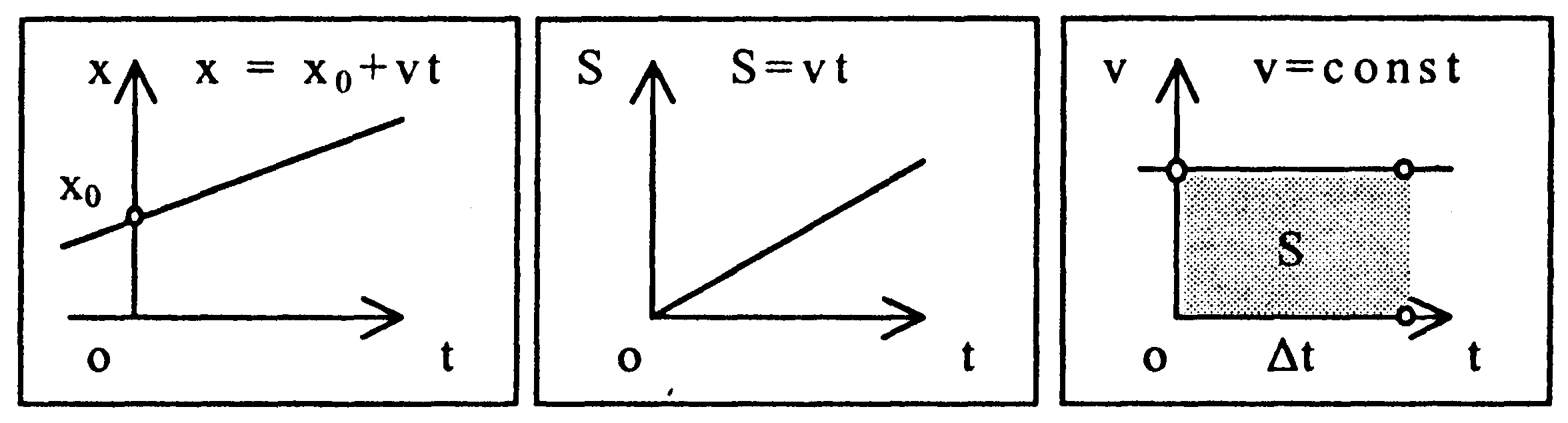
| |||||||||||||||||||||||||||
РАВНОПЕРЕМЕННОЕ ПРЯМОЛИНЕЙНОЕ
движение
 
| † прямолинейное движение материальной точки, при котором ее ускорение  с течением времени остается постоянным; с течением времени остается постоянным;
| |||||||||||||||||||||||||||
РАВНОУСКОРЕННОЕ прямолинейноедвижение† движение, при котором за любые равные промежутки времени скорость материальной точки увеличивается на одну и ту же величину

| РАВНОЗАМЕДЛЕННОЕ прямолинейноедвижение† движение, при котором за любые равные промежутки времени, скорость материальной точки уменьшается на одну и ту же величину

| |||||||||||||||||||||||||||
Среднее ускорение
 [м/с2] [м/с2]
| †  -изменение скорости за промежуток
времени -изменение скорости за промежуток
времени  ;
† векторная физическая величина; ;
† векторная физическая величина;
| |||||||||||||||||||||||||||
Мгновенное ускорение
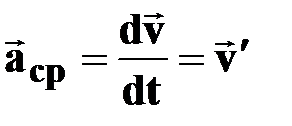 [м/с2] [м/с2]
|
†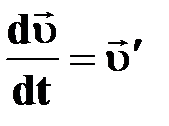 первая производная скорости по времени; первая производная скорости по времени;
| |||||||||||||||||||||||||||
Уравнение скорости
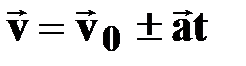 [м/с] [м/с]
| † векторная форма записи; | |||||||||||||||||||||||||||
Уравнение координаты

| † векторная форма записи;
† в проекциях на ось ОХ: х0>0, v0>0, a>0,
т.к. векторы  сонаправлены с осью ОХ;
† в проекциях на ось ОХ: х0>0, v0>0, a<0,
т.к. векторы сонаправлены с осью ОХ;
† в проекциях на ось ОХ: х0>0, v0>0, a<0,
т.к. векторы  сонаправлены с осью ОХ; вектор сонаправлены с осью ОХ; вектор  направлен противоположно оси ОХ; направлен противоположно оси ОХ;
| |||||||||||||||||||||||||||
| Уравнение пути |  [м] [м]
| |||||||||||||||||||||||||||
| Графическое представление равноускоренного прямолинейного движения | 
| |||||||||||||||||||||||||||
| Графическое представление равнозамедленного прямолинейного движения | 
| |||||||||||||||||||||||||||
| СВОБОДНОЕ ПАДЕНИЕ ТЕЛ † движение тела под действием силы тяжести; † свободное падение является равнопеременным движением (пренебрегая со противлением воздуха); | ||||||||||||||||||||||||||||
| ● ускорение свободного падения g = 9,81 м/с2 | † всегда направлено к центру Земли;
† gсонаправлено с ОУ;
 <0 - равнозамедленное –
при движении вверх; <0 - равнозамедленное –
при движении вверх;
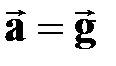 >0 - равноускоренное –
при движении вниз; >0 - равноускоренное –
при движении вниз;
| |||||||||||||||||||||||||||
| ● уравнение координаты | 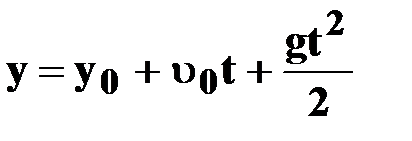
| 
| 
| |||||||||||||||||||||||||
| ● уравнение пути (S=h) |  
|  
| ||||||||||||||||||||||||||
| ● уравнение скорости | 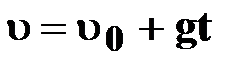
| 
| ||||||||||||||||||||||||||

| 
| |||||||||||||||||||||||||||
| ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО ВЕРТИКАЛЬНО ВВЕРХ | ||||||||||||||||||||||||||||
| ● уравнение координаты а=-g= - 9,81 м/с2 | 
| |||||||||||||||||||||||||||
| ● уравнение пути (S=h) |  
| |||||||||||||||||||||||||||
| ● уравнение скорости |  ; ;
| При   за время
за время
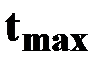 ,
тело достигнет максимальной высоты ,
тело достигнет максимальной высоты
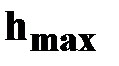
| 
| |||||||||||||||||||||||||
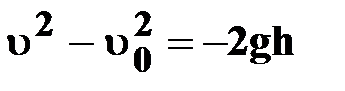
| 
| |||||||||||||||||||||||||||
| ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО ГОРИЗОНТАЛЬНО | ||||||||||||||||||||||||||||
| Закон независимости движений | † если материальная точка участвует одновременно в нескольких движениях, то результирующее перемещение точки равно векторной сумме перемещений, совершаемых ею в каждом движении. | |||||||||||||||||||||||||||
➨ вдоль оси ОХ – равномерное движение ( )
➨ вдоль ОУ – свободное падение ( )
➨ вдоль ОУ – свободное падение ( ) )
| ||||||||||||||||||||||||||||
| ● мгновенная скорость | 
| 
| ||||||||||||||||||||||||||
| ● горизонтальная скорость | 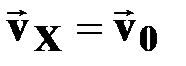
| |||||||||||||||||||||||||||
| ● вертикальная скорость | 
| |||||||||||||||||||||||||||
| ● модуль скорости | 
| |||||||||||||||||||||||||||
| ● уравнение координат точки | 
| 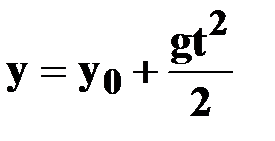
|  g = 9,81 м/с2
g = 9,81 м/с2
| |||||||||||||||||||||||||
| ● уравнение пути (S=h) | 
|  
| ||||||||||||||||||||||||||
| ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО ПОД УГЛОМ К ГОРИЗОНТУ | ||||||||||||||||||||||||||||
➨ вдоль оси ОХ – равномерное движение  ➨ вдоль ОУ – равнопеременное движение
➨ вдоль ОУ – равнопеременное движение 
| ||||||||||||||||||||||||||||
до высоты  :
движение
равнозамедленное,
затем –
равноускоренное. :
движение
равнозамедленное,
затем –
равноускоренное.
| 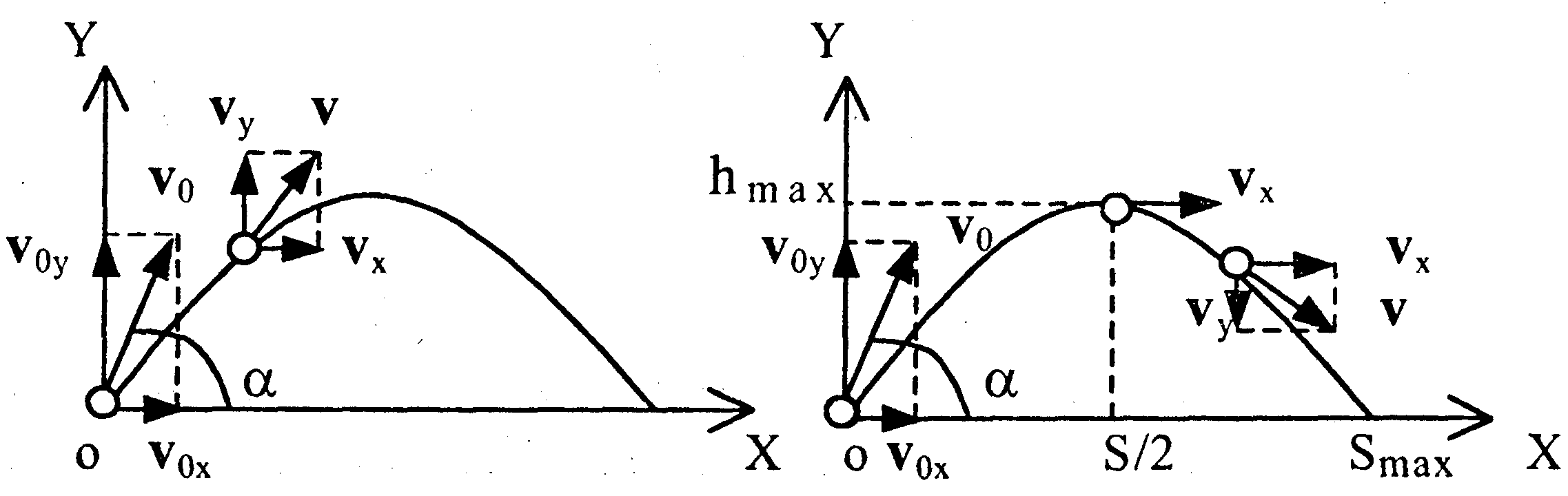
| |||||||||||||||||||||||||||
| ● уравнения координат точки | 
| 
| ||||||||||||||||||||||||||
| ● уравнения перемещений | 
| 
| ||||||||||||||||||||||||||
| ● уравнения скорости | 
| 
| ||||||||||||||||||||||||||
| ● модуль скорости | 
| |||||||||||||||||||||||||||
● время подъема на
максимальную высоту

| 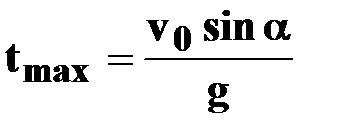
| |||||||||||||||||||||||||||
| ● максимальная высота подъема | 
| |||||||||||||||||||||||||||
| ● максимальный путь | 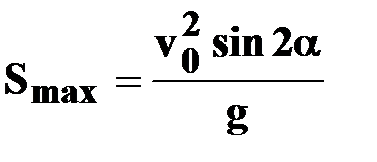
| |||||||||||||||||||||||||||
| РАВНОМЕРНОЕ ДВИЖЕНИЕ ПО ОКРУЖНОСТИ | ||||||||||||||||||||||||||||
| Движение по окружности | † точка Мдвижется по окружности радиуса R. За время tточка прошла дугуМ1М2. Радиус поворачивается на угол  ; ;
| 
| ||||||||||||||||||||||||||
● частота вращения
 
| † физическая величина, равная отношению количества  оборотов ко времени оборотов ко времени 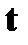 , за которое они совершены; , за которое они совершены;
| |||||||||||||||||||||||||||
| ● единица частоты Герц [Гц] | † частота, при которой тело совершает один оборот за одну секунду; | |||||||||||||||||||||||||||
● период вращения
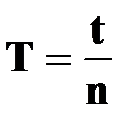 [с] [с]
| † время, за которое точка совершает один полный оборот вокруг оси вращения (на угол  радиан) радиан)
   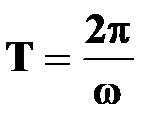
| |||||||||||||||||||||||||||
● радиан (рад)
(единица плоского угла)
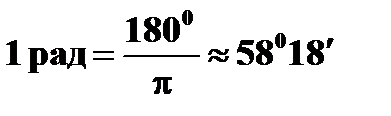

| † равен углу между двумя радиусами окружности, длина дуги между которыми равна радиусу. В градусном исчислении: | 
| ||||||||||||||||||||||||||
● угловая скорость
 
| † физическая величина, равная отношению угла поворота  ко времени ко времени  , за которое поворот произошел;
† при одном обороте точка М опишет угол , за которое поворот произошел;
† при одном обороте точка М опишет угол
 радиан радиан 
  
| |||||||||||||||||||||||||||
— линейная скорость
 или или 
| † линейная скорость точки, равномерно движущейся по окружности, оставаясь постоянной по модулю, непрерывно изменяется по направлению и в любой точке направлена по касательной к траектории;
†  ( ( - длина окружности) - длина окружности) 
| |||||||||||||||||||||||||||
| — связь между линейной и угловой скоростью | † 
| |||||||||||||||||||||||||||
Центростремительное
ускорение
 или
или

| † при равномерном движении тела по окружности его ускорение постоянно по модулю и в любой точке направлено по радиусу к центру окружности; | |||||||||||||||||||||||||||
● вывод формулы
центростремительного
ускорения

| † в момент времени 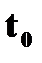 тело находилось в точке А и имело скорость тело находилось в точке А и имело скорость  . Через промежуток времени . Через промежуток времени  оно переместилось в точку В и имело скорость оно переместилось в точку В и имело скорость  .
Изменение скорости найдем по правилу вычитания векторов: в точку В перенесем вектор .
Изменение скорости найдем по правилу вычитания векторов: в точку В перенесем вектор  и вычтем его из вектора и вычтем его из вектора  (что равноценно сложению векторов (что равноценно сложению векторов  и и  ).
Треугольники АОВ и ВСD подобны и имеют равные углы ).
Треугольники АОВ и ВСD подобны и имеют равные углы  АОВ= АОВ=  СВD (углы со взаимно перпендикулярными сторонами) СВD (углы со взаимно перпендикулярными сторонами)  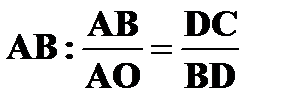 .
Хорда АВ мала, поэтому ее можно заменить дугой АВ, длина которой равна: АВ= .
Хорда АВ мала, поэтому ее можно заменить дугой АВ, длина которой равна: АВ=  (т.е. произведение скорости на время движения тела от точки А до точки В).
Т.к. АО=R, DC= (т.е. произведение скорости на время движения тела от точки А до точки В).
Т.к. АО=R, DC=  BD=
BD=    ; ; 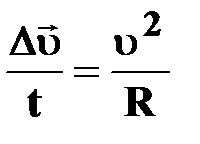 ; ;  
 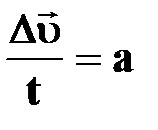  
| |||||||||||||||||||||||||||
| ЛЕКЦИЯ 2 ВРАЩАТЕЛЬНОЕ движение движение, при котором траектории всех точек вращающегося тела являются окружностями, центры которых лежат на одной оси, называемой осью вращения | ||||||||||||||||||||||||||||
| АНАЛОГИЯ между ПОСТУПАТЕЛЬНЫМ и ВРАЩАТЕЛЬНЫМ движениями Кинематические характеристики движения | ||||||||||||||||||||||||||||
| ПОСТУПАТЕЛЬНОЕ движение | ВРАЩАТЕЛЬНОЕ движение | |||||||||||||||||||||||||||
| Путь | S | м | Угол поворота | j | рад | |||||||||||||||||||||||
| Время | t | с | Время | T | с | |||||||||||||||||||||||
| Cкорость | υ | м/с | Угловая скорость | w | рад/с | |||||||||||||||||||||||
| Ускорение | а | м/с2 | Угловое Ускорение | e | рад/с2 | |||||||||||||||||||||||
| Основные кинематические характеристики ВРАЩАТЕЛЬНОГО движения | ||||||||||||||||||||||||||||
| УГЛОВАЯ СКОРОСТЬ | † характеризует быстроту ращения тела; † векторная величина; | |||||||||||||||||||||||||||
Средняя
угловая скорость
 [рад/с] [рад/с]
| †отношение угла поворота  радиус-вектора точки за промежуток времени радиус-вектора точки за промежуток времени  к длительности этого промежутка:
† векторная величина, к длительности этого промежутка:
† векторная величина,
| 
| ||||||||||||||||||||||||||
Мгновенная
угловая скорость
 [рад/с] [рад/с]
| † вектор, определяемый первой производной угла поворота тела по времени

| 
| ||||||||||||||||||||||||||
| Направление угловой скорости (правило правого винта) | † вектор угловой скорости  совпадает по направлению с поступательным движением острия винта, который вращается в направлении движения точки по окружности. совпадает по направлению с поступательным движением острия винта, который вращается в направлении движения точки по окружности.
| |||||||||||||||||||||||||||
| — радиан в секунду (рад/с) | † равен угловой скорости равномерно вращающегося тела, все точки которого за 1 с поворачиваются на угол 1 рад. | |||||||||||||||||||||||||||
Период вращения
 [с] [с]
| † время, за которое точка совершает один полный оборот вокруг оси вращения, т.е. поворачивается на угол  радиан;
† так как промежутку времени радиан;
† так как промежутку времени  соответствует соответствует  , то , то

| |||||||||||||||||||||||||||
Частота вращения
 [c-1] [c-1]
| †число полных оборотов, совершаемых телом при его равномерном движении;
† 
| |||||||||||||||||||||||||||
УГЛОВОЕ УСКОРЕНИЕ
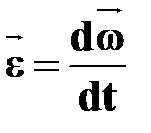 [рад/с2] [рад/с2]
| †векторная величина, равная первой производной угловой скорости по времени: | |||||||||||||||||||||||||||
| — радиан на секунду в квадрате (рад/с2) | † равен угловому ускорению равноускоренно вращающегося тела, при котором оно за 1с изменяет угловую скорость на 1 рад/с; | |||||||||||||||||||||||||||
| Направление углового ускорения | †вектор углового ускорения 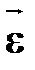 направлен по оси вращения в сторону вектора элементарного приращения угловой скорости; направлен по оси вращения в сторону вектора элементарного приращения угловой скорости;
| |||||||||||||||||||||||||||

| ||||||||||||||||||||||||||||
при ускоренном движении вектор 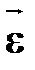 параллелен вектору
параллелен вектору 
| при з амедленном – антипараллелен | |||||||||||||||||||||||||||
| Связь между линейными и угловыми характеристиками | † связь между длиной пути S, пройденного точкой по окружности радиуса R и углом поворота φ S=φ·R [м] †связь между линейной скоростью vи угловой скоростью ω v=ω·R[м/с] | |||||||||||||||||||||||||||
Равномерное
вращение
ω=const;  =0 =0
| Равно ускоренное и равно замедленное
вращение
ω≠const;  >0 и ω≠const; >0 и ω≠const;  <0 <0
| |||||||||||||||||||||||||||
Уравнение координаты

| Уравнение координаты

| Уравнение скорости

| ||||||||||||||||||||||||||
φ– угол поворота;
 - начальное угловое перемещение;
t – время; - начальное угловое перемещение;
t – время;
 - начальная угловая скорость;
ε-угловое ускорение; - начальная угловая скорость;
ε-угловое ускорение;
| ||||||||||||||||||||||||||||

Поиск:
Рекомендуем:
 Почему я выбрал профессую экономиста
Почему я выбрал профессую экономиста
 Почему одни успешнее, чем другие
Почему одни успешнее, чем другие
 Периферийные устройства ЭВМ
Периферийные устройства ЭВМ
 Нейроглия (или проще глия, глиальные клетки)
Нейроглия (или проще глия, глиальные клетки)
Категории:
ПОСТУПАТЕЛЬНОГО движения
|
|
|
|
|
|
|
|
|
|
Дата добавления: 2015-10-01; Мы поможем в написании ваших работ!; просмотров: 896 | Нарушение авторских прав
Поиск на сайте:
Лучшие изречения:

