| “ема 3
| —»Ћџ ¬ ћ≈’јЌ» ≈
|
| ¬ задачах механики учитываютс€ силы:
| ➨ гравитационные - uсилы т€готени€;
➨ электромагнитные - vсилы упругости;
wсилы трени€.
|
| u —»Ћџ
“я√ќ“≈Ќ»я
(гравитационные силы)
| ➨ вс€кое тело, имеющее массу, €вл€етс€ источником гравитационного пол€ Ц пол€ т€готени€. „ерез гравитационное поле осуществл€етс€ гравитационное взаимодействие;
➨ гравитационные силы (силы т€готени€) могут быть только силами прит€жени€;
|
«акон всемирного т€готени€
(».Ќьютон, 1687 г.)

| ➨ тела прит€гиваютс€ друг к другу с силой, модуль которой пр€мо пропорционален произведению их масс, обратно пропорционален квадрату рассто€ни€ между ними и направлен вдоль линии, соедин€ющей центры этих тел;
| 
|
● гравитационна€
посто€нна€
G=  =
=6,67∙10-11 =
=6,67∙10-11 
| ➨ численно равна силе прит€жени€ между двум€ телами массой по 1 кг каждое, расположенными на рассто€нии 1 м друг от друга;
|
—»Ћј “я∆≈—“»
 =mg =mg
| ➨ сила прит€жени€ тела к «емле.
➨ сила т€жести Ц это сила т€готени€; гравитационна€ сила; приложена к телу;
|
| ● свободное падение
| ➨ равноускоренное движение, совершаемое под действием силы т€жести в безвоздушном пространстве (вакууме);
|
● ускорение
свободного
падени€
ѕо II закону Ќьютона:  
| ➨ ускорение, сообщаемое телу силой т€жести;
|
1) g не зависит от массы тела;
2) g зависит от массы «емли  (на разных планетах разное);
3) g зависит от квадрата радиуса «емли (на разных планетах разное);
3) g зависит от квадрата радиуса «емли  ;
● на экваторе gЁ= 9,78 м/с2;
● на полюсе gѕ= 9,83 м/с2;
● на широте ;
● на экваторе gЁ= 9,78 м/с2;
● на полюсе gѕ= 9,83 м/с2;
● на широте  g = 9,80 м/с2; g = 9,80 м/с2;
|
 ¬≈— “≈Ћј ¬≈— “≈Ћј
 [H] [H]
| ➨ сила, с которой тело, вследствие его прит€жени€ в «емле, действует горизонтально на опору или раст€гивает подвес.
➨ вес тела приложен к опоре или подвесу, (а сила т€жести приложена к телу);
➨вес тела численно равен силе упругости;
|
 ¬ес тела, движущегос€ с ускорением ¬ес тела, движущегос€ с ускорением
|
| ● невесомость
–=0
| ➨ исчезновение веса при движении опоры вниз с ускорением свободного падени€, т.е. а=g:
OY: ma=P-Fупр (P=Fупр)
ma=mg-P
P=mg-ma
P=m(g-a), т.к. а=g, то –=0
|
|
| ● перегрузка
P=m(g+a)
| ➨ увеличение веса тела, вызванное ускоренным движением опоры или подвеса вверх:
OY: -ma=P-Fупр (P=Fупр)
-ma=mg-P
P=mg+ma
P=m(g+a)
| 
|
| ● вес равен
силе т€жести
–=mg
| ➨ если опора (или подвес) неподвижны или движутс€ равномерно и пр€молинейно относительно «емли, то вес тела равен силе т€жести.
|
ѕерва€ космическа€
скорость
  км/с км/с
| ➨ горизонтально направленна€ минимальна€ скорость, с которой тело могло бы двигатьс€ вокруг земли по круговой орбите, т.е. превратитьс€ в искусственный спутник земли;
|
| ● вывод первой
космической
скорости
| Fт=Fцс (движение по круговой орбите)
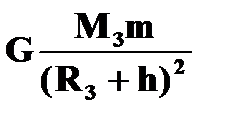 = = 
 , т.к. h=0, , т.к. h=0,  , то , то 
| 

|
¬тора€ космическа€ скорость
 11,2 км/с 11,2 км/с
| ➨ наименьша€ скорость, которую надо сообщить телу, чтобы его орбита в поле т€готени€ «емли стала параболической, т.е. чтобы тело могло превратитьс€ в спутник —олнца.
| |
| “реть€ космическа€
скорость
v3 = 16,7 км/с
| ➨ скорость, которую необходимо сообщить телу на «емле, чтобы оно покинуло пределы —олнечной системы.
|
| v —»Ћџ
”ѕ–”√ќ—“»
| ➨ силы, возникающие внутри вещества при деформации твердого тела, которые стрем€тс€ восстановить первоначальные размеры тела;
|
| ƒеформаци€
| ➨ изменение формы или объема тела при действии на него силы;
|
| ● упругие деформации
(раст€жение, сжатие, изгиб, сдвиг, кручение)
| ➨ деформации, при которых после прекращени€ действи€ внешних сил тело принимает первоначальные размеры и форму (пружина, ластик);
|
| ● пластические
деформации
| ➨ деформации, которые сохран€ютс€ в теле после прекращени€ действи€ внешних сил (пластилин);
|
«акон √ука
(–оберт √ук, 1660 г.)
 или
σ = ε∙ Ε
или
σ = ε∙ Ε

| ➨ сила упругости, возникающа€ при деформации тела, пр€мо пропорциональна удлинению (деформации) тела и направлена в сторону, противоположную деформации;
➨k Ц жесткость пружины;
|

|
➨ при небольших деформаци€х напр€жение  пропорционально относительному удлинению пропорционально относительному удлинению  ; ;
|
| ● абсолютное
удлинение
∆ℓ =ℓ -ℓ0
| ➨ при упругом раст€жении стержн€ под действием силы он удлин€етс€ на величину ∆ℓ;
|
● относительное
удлинение
ε = 
| ➨ равно отношению абсолютного удлинени€ к длине всего стержн€;
➨ количественна€ мера, характеризующа€ степень деформации, испытываемой телом;
|
● напр€жение
σ =  [ѕа] [ѕа]
| ➨ сила, действующа€ на единицу площади поперечного сечени€;
|
| ● модуль ёнга (≈)
| ➨ равен нормальному напр€жению σ, при котором линейный размер тела измен€етс€ в два раза;
|
ƒиаграмма
напр€жений

| ➨ устанавливает св€зь между деформацией и напр€жением.
|
➨ σп - предел пропорциональности Ц линейна€ зависимость σ (ε) выполн€етс€ в узких пределах доσп;
➨ σу Ц предел упругости - остаточные деформации не возникают при увеличении напр€жени€ до σу;
➨ σт - предел текучести - напр€жение, при котором по€вл€етс€ заметна€ остаточна€ деформаци€;
➨ σр - предел прочности - максимальное напр€жение, возникающее в теле до разрушени€;
CD- область текучести или областьпластических деформаций.
 «а точкой D происходит разрушение тела. «а точкой D происходит разрушение тела.
|
| w —»Ћџ
“–≈Ќ»я
| ➨ сила сопротивлени€, действующа€ на тело и направленна€ противоположно относительному перемещению данного тела;
|
|
| Ј внешнее трение
(сухое)
| ➨ трение, возникающее в плоскости касани€ двух соприкасающихс€ тел при их относительном перемещении (трение поко€; трение качени€; трение скольжени€).
|
▪ силатрени€ поко€

| ➨ сила, котора€ возникает между соприкасающимис€ и поко€щимис€ одно относительно другого телами;
➨ максимальна€ сила трени€ поко€ пропорциональна силе нормального давлени€;
|
▪ силатрени€
скольжени€

| ➨ сила, котора€ возникает между соприкасающимис€ и движущимис€ одно относительно другого телами.
▪  поко€ > поко€ >  скольжени€;
▪ скольжени€;
▪  > >  ▪
▪  зависит от рода и шероховатости трущихс€ поверхностей; безразмерна€ величина; зависит от рода и шероховатости трущихс€ поверхностей; безразмерна€ величина;
|
▪ силатрени€ качени€

| ➨ сила, возникающа€ между соприкасающимис€ и кат€щимис€ друг относительно друга телами;
➨ R Ц радиус кат€щегос€ колеса;
|
| Ј внутреннее трение
(жидкое или в€зкое)
| ➨ трение между част€ми одного и того же тела, например, между различными сло€ми жидкости или газа, скорости которых мен€ютс€ от сло€ к слою.
|
| ▪ силажидкостного
трени€
| ➨ сила возникает при движении тела в жидкости.
▪  жидкостного зависит от площади поперечного сечени€ и формы тела;
▪ жидкостного зависит от площади поперечного сечени€ и формы тела;
▪  скольжени€ > скольжени€ >  жидкостного. жидкостного.
|
| «начение силы трени€
|
|
| ● достоинства
| ➨ благодар€ трению движетс€ транспорт, удерживаетс€ вбитый в стену гвоздь, ход€т люди и т.д.
|
| ● недостатки
| ➨ дл€ уменьшени€ силы трени€ необходимо:
▪ на трущиес€ поверхности нанести смазку (сила трени€ уменьшаетс€ почти в 10 раз), т.е. внешнее трение замен€етс€ значительно меньшим внутренним трением ( > >  );
▪ устанавливают шариковые и роликовые подшипники, т.е. замен€ют трение скольжени€ трением качени€ ( );
▪ устанавливают шариковые и роликовые подшипники, т.е. замен€ют трение скольжени€ трением качени€ ( ) )
|
 ƒвижение тела с учетом силы трени€ ƒвижение тела с учетом силы трени€
|
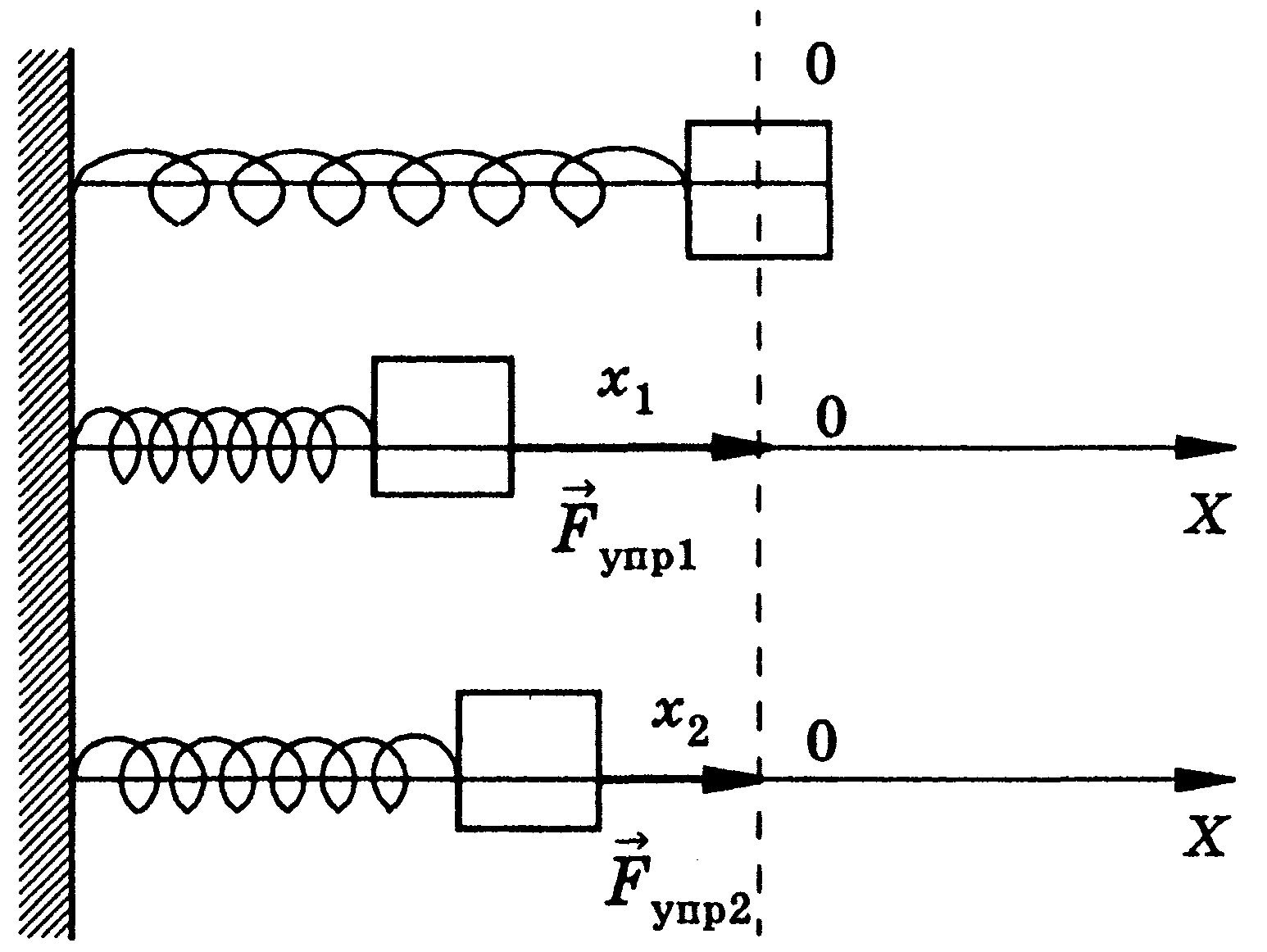
| ● движение по
горизонтальной
поверхности
| ➨ OX: ma=F-Fтр
OY:0=N-mg  N=mg;
Fтр= N=mg;
Fтр=  N= N=  mg mg
  ; ;
|
| ● движение
по наклонной
плоскости
(тело скользит)
| ➨ OX: ma=mg sin  -Fтр
OY:0=N-mgcos -Fтр
OY:0=N-mgcos   N=mg cos N=mg cos  ;
Fтр= ;
Fтр=  N= N=  mg cos mg cos 
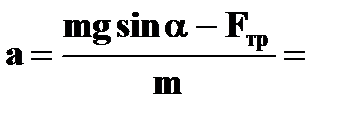 =
=  = g(sin
= g(sin  - -  ); );
|
| | | | | | | | | |
| “ема 4
| «ј ќЌџ —ќ’–јЌ≈Ќ»я
|
«акон сохранени€
импульса («—»)

| ➨ векторна€ сумма импульсов тел, вход€щих в замкнутую систему, остаетс€ посто€нной при любых взаимодействи€х тел этой системы между собой;
|
| Ј замкнута€ система
| ➨ механическа€ система, на которую не действуют внешние силы;
|
| Ј внешние силы
| ➨ силы, которые действуют на тела системы со стороны других тел;
|
| Ј внутренние силы
| ➨ силы, с которыми тела, вход€щие в систему, взаимодействуют между собой;
|
Ј абсолютно
упругий удар
 =
= 
| ➨ столкновение двух тел, в результате которого в обоих взаимодействующих телах не остаетс€ никаких деформаций и вс€ кинетическа€ энерги€, которой обладали тела до удара, снова превращаетс€ в кинетическую энергию;
| 
|
Ј абсолютно
неупругий удар
 

| ➨ столкновение двух тел, в результате которого тела объедин€ютс€, двига€сь дальше как единое целое;
| 
|
| ● удар (соударение)
| ➨ встреча двух или более тел, при которой взаимодействие длитс€ очень короткое врем€.
|
 –акета –акета
| ➨ люба€ ракета имеет трубчатый корпус, передний конец которого закрыт обтекателем, а другой представл€ет собой сопло.
—хема ракеты: 1 Ц головна€ часть ракеты, в которой расположен полезный груз; 2Ц баки с топливом;3 Ц камера сгорани€ топлива;
4Ц реактивное сопло, из которого с большой скоростью вырываютс€ газы, в результате чего возникает реактивна€ сила - сила реакции (отдачи) струи рабочего газа.
ƒвижение ракет - пример реактивного движени€.
|
| ● реактивное
движение (–ƒ)
| ➨ движение тела, возникающее вследствие отделени€ от него части его массы с некоторой скоростью. ƒл€ осуществлени€ –ƒ не требуетс€ взаимодействи€ тела с окружающей средой, т.к. оно осуществл€етс€ в результате взаимодействи€ с газами, образующимис€ при сгорании топлива;
|
| | ● скорость ракеты


| ➨ по «—» сумма импульсов корпуса ракеты и вытекающих из нее газов равна суммарному импульсу ракеты на старте, который равен нулю.
—ледовательно: 0=  , отсюда , отсюда
    / ћр
«нак Ђ‒ї показывает, что направление скорости ракеты противоположно направлению скорости вылетающих газов.
—корость ракеты
можно увеличить двум€ способами:
1) увеличить скорость / ћр
«нак Ђ‒ї показывает, что направление скорости ракеты противоположно направлению скорости вылетающих газов.
—корость ракеты
можно увеличить двум€ способами:
1) увеличить скорость  газов, вытекающих из сопла ракеты;
2) увеличить массу сгораемого топлива газов, вытекающих из сопла ракеты;
2) увеличить массу сгораемого топлива  , что приводит к уменьшению полезной нагрузки Ц массы груза ракеты. , что приводит к уменьшению полезной нагрузки Ц массы груза ракеты.
|
| | ● основоположники
космонавтики
| ➨ .Ё. ÷иолковский Ц научно обосновал применение ракет дл€ космических полетов, использование в качестве горючего жидкое топливо, многоступенчатые ракеты;
—.ѕ. оролев Ц руководитель запуска в нашей стране первого в мире искусственного спутника «емли (4.10.1957); ё.ј. √агарин - первый космонавт (12.04.1961)
|
| | ћ≈’јЌ»„≈— јя –јЅќ“ј
 ј=FЈS cos α ј=FЈS cos α
| ➨ скал€рна€ физическа€ величина, равна€ произведению модулей векторов силы  и перемещени€ и перемещени€  , умноженному на косинус угла , умноженному на косинус угла  между этими векторами; между этими векторами;
|
| | | 
| ➨   - работа положительна€ - работа положительна€
|
| | 
| ➨   - работа равна нулю - работа равна нулю
|
| | 
| ➨  , ,  - работа отрицательна€ - работа отрицательна€
|
| | ● единица работы
1 ƒжоуль
| ➨ работа, совершаема€ силой в 1 Ќ на пути в 1 м
1ƒж = 1Ќ×м
|
| | ● работа переменной
силы
|
➨  = = 
|
| | ● работа силы т€жести
|
➨  ➨ равна произведению силы т€жести на разность высот в начальном
➨ равна произведению силы т€жести на разность высот в начальном  и конечном и конечном  положени€х тела;
➨ не зависит от длины и формы пути, пройденного телом; положени€х тела;
➨ не зависит от длины и формы пути, пройденного телом;
| 
|
| | ● работа
силы упругости

|
➨ 
| 
|
| | ● работа
силы трени€
| ➨  < 0, т.к. направлени€ векторов силы и перемещени€ противоположны. < 0, т.к. направлени€ векторов силы и перемещени€ противоположны.
|
| | ћќўЌќ—“№
 [¬т] [¬т]
| ➨ скал€рна€ физическа€ величина, равна€ отношению работы к промежутку времени, за который она совершена;
➨ характеризует быстроту совершени€ работы;
|
| | ● мощность при
равномерном
движении
N= Fs×v
| ➨ если тело движетс€ с посто€нной скоростью (v=const), то мощность равна произведению проекции силы на направление перемещени€, умноженному на скорость тела;
|
| | ● единица мощности
1 ¬атт
| ➨ мощность, при которой за врем€ 1 с совершаетс€ работа в 1 ƒж:
1 ¬т = 1 ƒж/с
|
| | ћ≈’јЌ»„≈— јя ЁЌ≈–√»я
| ➨ скал€рна€ количественна€ мера движени€ и взаимодействи€ всех видов материи, способность совершать работу;
|
| | »Ќ≈“»„≈— јя энерги€
≈к =  [ƒж] [ƒж]
| ➨ энерги€, которой обладает движущеес€ тело. ќна равна половине произведени€ массы тела на квадрат его скорости;
|
| | ѕќ“≈Ќ÷»јЋ№Ќјя энерги€
≈р = mgh [ƒж]
| ➨ энерги€, обусловленна€ взаимным расположением тел или частей тела, завис€ща€ от их взаимного положени€ во внешнем силовом (например, гравитационном) поле;
|
| | ● потенциальна€
энерги€
силы т€жести
≈р = –h = mgh
| ➨ энерги€ возможного действи€ гравитационного пол€ «емли на материальную точку, расположенную на высотеhнад уровнем мор€;
➨ физическа€ величина, численно равна€ произведению силы т€жести –на высоту h;
|
| | ● потенциальна€
энерги€
упругой деформации

| ➨ запас энергии деформированного упругого тела ➨ физическа€ величина, численно равна€ половине произведени€ коэффициента упругости тела k на квадрат деформации;
|
| | ѕќЋЌјя
механическа€
энерги€
≈полн. = ≈к + ≈р
| ➨ равна сумме кинетической и потенциальной энергий;
|
| | ➨ падающего
тела
| ➨ упруго деформированного
тела
|
| | ≈полн. = 
| ≈полн 
|
| | «акон сохранени€
механической энергии
≈к + ≈р = const

| ➨ в замкнутой системе тел, между которыми действуют только консервативные силы, механическа€ энерги€ сохран€етс€, т.е. не измен€етс€ со временем;
|
| | «акон сохранени€
и превращени€
энергии
| ➨ энерги€ никогда не исчезает и не по€вл€етс€ вновь, она лишь превращаетс€ из одного вида в другой;
|
| | ѕ–ќ—“џ≈
ћ≈’јЌ»«ћџ
| ➨ механизмы, позвол€ющие получить выигрыш в силе;
|
| | ● Ђзолотоеї правило
механики
| ➨ при совершении одной и той же работы во сколько раз мы выигрываем в силе, во столько же раз проигрываем в рассто€нии;
|
| | ● рычаг
| ➨ твердое тело, вращающеес€ вокруг неподвижной оси и позвол€ющее меньшей силой  уравновесить большую силу уравновесить большую силу  ; ;
|
| | Ј правило рычага

| ➨ рычаг находитс€ в равновесии, если отношение прилагаемых сил обратно пропорционально отношению плеч;
| 
|
| | ● блок
| ➨ колесо с желобом, в который пропущена веревка (трос, цепь, ремень);
|
| | ● неподвижный блок➨ позвол€ет изменить направлени€ действи€ силы, однако не дает выигрыша в силе
|  ● подвижный блок➨ дает выигрыш в силе в два раза ● подвижный блок➨ дает выигрыш в силе в два раза
|
| | 
| 
| | 
|
| | ● наклонна€ плоскость
➨ дает выигрыш в силе во столько раз, во сколько раз ее длина больше высоты подъема.
| 
|
| | оэффициент полезного
действи€ ѕƒ
 [%] [%]

| ➨ величина, равна€ отношению полезной работы ко всей затраченной работе и ли
➨ отношение полезной мощности ко всей подводимой к механизму мощности
|
| | ● полезна€ работа
| ➨ работа, совершенна€ с использованием механизмов;
|
| | ● затраченна€ работа

| ➨ дополнительна€ работа, например, работа по преодолению трени€ в ос€х, по перемещению механизма;
➨ затраченна€ работа всегда больше полезной работы;
|
| | | “ема 5
| ќ—Ќќ¬џ —ѕ≈÷»јЋ№Ќќ… “≈ќ–»»
ќ“Ќќ—»“≈Ћ№Ќќ—“»
| | -представл€ет собой современную физическую теорию пространства и времени;
| | —пециальна€ теории относительности
(—“ќ)
| ➨предложена немецким физиком ј.Ёйнштейном (1905 г.) дл€ согласовани€ экспериментальных данных по измерению скорости света с теоретической базой классической (ньютоновской) механики.
➨ —“ќ рассматривает €влени€, происход€щие только в инерциальных системах отсчета.
➨ —“ќ часто называетс€ рел€тивистской теорией.
| | ѕостулаты теории относительности
| ➨ теори€ относительности базируетс€ на двух постулатах.
➨ справедливость постулатов доказываетс€ тем, что следстви€, вытекающие из постулатов, хорошо согласуютс€ с результатами многочисленных экспериментов (например, движение элементарных частиц в ускорител€х).
| | ❶ принцип
относительности
Ёйнштейна
| ➨ при одних и тех же услови€х все физические €влени€ в любой инерциальной системе отсчета происход€т совер-шенно одинаково.
| | ➨ это значит, что никакими экспериментами (механичес-кими, электромагнитными, оптическими и др.), поставлен-ными внутри инерциальной системы, невозможно устано-вить, покоитс€ эта система или движетс€ равномерно и пр€молинейно.
➨из данного постулата следует, что при переходе из одной инерциальной системы отсчета к другой математические выражени€ законов физики не должны измен€тьс€.
| | ❷ принцип посто€нства
(инвариантности)
скорости света
| ➨ скорость света в вакууме не зависит от скорости движе-ни€ источников и приемников света и во всех инерциальных системах отсчета одинакова.
| | ➨ из данного постулата следует, что взаимодействи€ между телами в природе не могут распростран€тьс€ с бесконечно большой скоростью. —корость света в вакууме €вл€етс€ предельной скоростью передачи сигнала.
| | —ледстви€ постулатов теории относительности
| Ј относительность
рассто€ний

| ➨  - длина стержн€ в неподвижной системе отсчета, отно-сительно которой стержень покоитс€; - длина стержн€ в неподвижной системе отсчета, отно-сительно которой стержень покоитс€;
 - длина стержн€ в подвижной системе отсчета, относи-тельно которой стержень движетс€ со скоростью - длина стержн€ в подвижной системе отсчета, относи-тельно которой стержень движетс€ со скоростью  .
—окращение длины тем больше, чем больше скорость движени€.
ѕоперечные размеры тела не завис€т от скорости его движени€ и одинаковы во всех инерциальных системах отсчета. .
—окращение длины тем больше, чем больше скорость движени€.
ѕоперечные размеры тела не завис€т от скорости его движени€ и одинаковы во всех инерциальных системах отсчета.
| Ј относительность
промежутков времени

| ➨  - интервал времени между двум€ событи€ми, происход€-щими в одной и той же точке неподвижной системы отсчета;
➨ - интервал времени между двум€ событи€ми, происход€-щими в одной и той же точке неподвижной системы отсчета;
➨  - интервал между этими же событи€ми в подвижной системе отсчета, движущейс€ относительно неподвижной со скоростью - интервал между этими же событи€ми в подвижной системе отсчета, движущейс€ относительно неподвижной со скоростью  .
ƒлительность событи€, происход€щего в некоторой точке, наименьша€ в той инерциальной системе отсчета, относительно которой эта точка неподвижна.
“аким образом, ход часов замедл€етс€ в системе отсчета, относительно которой часы движутс€. .
ƒлительность событи€, происход€щего в некоторой точке, наименьша€ в той инерциальной системе отсчета, относительно которой эта точка неподвижна.
“аким образом, ход часов замедл€етс€ в системе отсчета, относительно которой часы движутс€.
| Ј рел€тивистский закон
сложени€ скоростей

| ➨  - подвижна€ система отсчета, котора€ движетс€ со скоростью - подвижна€ система отсчета, котора€ движетс€ со скоростью  вдоль оси ќ’ относительно неподвижной системы отсчета .
➨точкаћдвижетс€ со скоростью вдоль оси ќ’ относительно неподвижной системы отсчета .
➨точкаћдвижетс€ со скоростью  вдоль оси вдоль оси  подвижной системы подвижной системы  . .
| 
| «ависимость массы от скорости (рел€тивистска€ масса)

| ➨ 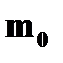 - масса поко€щегос€ тела; масса поко€ €вл€етс€ величиной, одинаковой дл€ всех систем отсчета, в которых тело покоитс€.
➨ - масса поко€щегос€ тела; масса поко€ €вл€етс€ величиной, одинаковой дл€ всех систем отсчета, в которых тело покоитс€.
➨  - масса того же тела, но движущегос€ со скоростью - масса того же тела, но движущегос€ со скоростью  .
ѕри увеличении скорости тела его масса .
ѕри увеличении скорости тела его масса  возрастает. возрастает.
| –ел€тивистский
импульс

| ➨ рел€тивистский импульс пропорционален вектору скорости.
| | «акон сохранени€ рел€тивистского импульса
| ➨ рел€тивистский импульс замкнутой системы сохран€етс€, т.е. не измен€етс€ с течением времени.
| | ќсновной закон рел€тивистской
| ➨ вектор результирующей силы  , приложенной к материальной точке (телу), равен изменению вектора рел€тивистского импульса , приложенной к материальной точке (телу), равен изменению вектора рел€тивистского импульса  тела (или материальной точки) за единицу времени тела (или материальной точки) за единицу времени
| | динамики
| 
| —в€зь между
массой и энергией

| ➨ полна€ энерги€ тела или системы тел равна произведению ее полной рел€тивистской массы на квадрат скорости света в вакууме.
| Ёнерги€ поко€

| ➨ энерги€, которой обладает неподвижное тело;
➨ энерги€ поко€ Ц это внутренн€€ энерги€ тела.
| | инетическа€
энерги€ тела
| ➨ представл€ет собой разность между полной энергией тела  и энергией поко€ и энергией поко€  . .
| | | | | | | |
| | “ема 6
| ћ≈’јЌ» ј ∆»ƒ ќ—“≈… » √ј«ќ¬
|
| | ƒј¬Ћ≈Ќ»≈
 [ѕа] [ѕа]
| ➨ физическа€ величина, численно равна€ отношению модул€ силы F, действующей перпендикул€рно поверхности, к площади S этой поверхности;
|
| | ● единица давлени€ -
1 ѕаскаль
| ➨ давление, которое производит сила 1Ќ на перпендикул€рную к ней поверхность площадью 1 м2
1 ѕа = 1 Ќ/м2
|
| | ● внесистемные
единицы
| ➨ физическа€ атмосфера (атм):
1атм = 105 ѕа (нормальное атмосферное давление);
➨ миллиметр ртутного столба (мм рт. ст.):
1атм = 760 мм рт. ст.
|
| | јтмосферное давление
| ➨ давление, оказываемое атмосферой на все наход€щиес€ в ней предметы;
|
| | ● атмосфера
| ➨ воздушна€ оболочка, состо€ща€ из смеси различных газов и вращающа€с€ вместе с «емлей как единое целое;
|
| | ● изменение атмосферного
давлени€
| ➨ атмосферное давление уменьшаетс€ с увеличением высоты подъема над «емлей;
|
| | ● измерение
давлени€:
- барометры
| ➨ приборы, предназначенные дл€ измерени€ атмосферного давлени€:
‒ ртутный барометр;
‒ барометр - анероид;
|
| | - манометры
| ➨ приборы, предназначенные дл€ измерени€ давлений жидкостей и газов:
‒ жидкостный открытый (U-образна€ трубка, открыта€ с обеих сторон);
‒ закрытый (U-образна€ трубка, запа€нна€ с одной стороны);
‒ металлический (трубчато-пружинный манометр);
‒ поршневой;
|
| | «ј ќЌ ѕј— јЋя
дл€ жидкостей и газов
(давление жидкости
на глубине  )
Ј гидростатическое давление
р=ρgh )
Ј гидростатическое давление
р=ρgh
| ➨ жидкость или газ передают производимое на них давление по всем направлени€м равномерно;
➨ равно произведению плотности жидкостиρ на модуль ускорени€ свободного падени€ g и на высоту h столба жидкости;
| 
|
| | ● сообщающиес€
сосуды
| ➨ сосуды, соединенные ниже уровн€ поверхности жидкости;
|
| | ● закон
сообщающихс€
сосудов
| ➨ однородна€ жидкость
ρ1=ρ2
устанавливаетс€ в сообщающихс€ сосудах на одном и том же уровне
h1 =h2
| 
| |
| | ➨ высоты столбов
разнородных жидкостей
 ,
наход€щихс€ в сообщающихс€ сосудах, обратно пропорциональны плотност€м этих жидкостей ,
наход€щихс€ в сообщающихс€ сосудах, обратно пропорциональны плотност€м этих жидкостей

|

| |
| | ● гидравлический пресс

| ➨ два сообщающихс€ сосуда, заполненные жидкостью (водой или маслом) и закрытые поршн€ми различной площади;
| |
| | ●  - гидравлический пресс дает выигрыш в силе, но проигрыш в длине пути поршн€;
● - гидравлический пресс дает выигрыш в силе, но проигрыш в длине пути поршн€;
●  - силы, действующие на поршни пропорциональны площад€м этих поршней; - силы, действующие на поршни пропорциональны площад€м этих поршней;
| |
| | | |
| | «акон јрхимеда
дл€ жидкостей и газов
Fјрх = ρж gVт
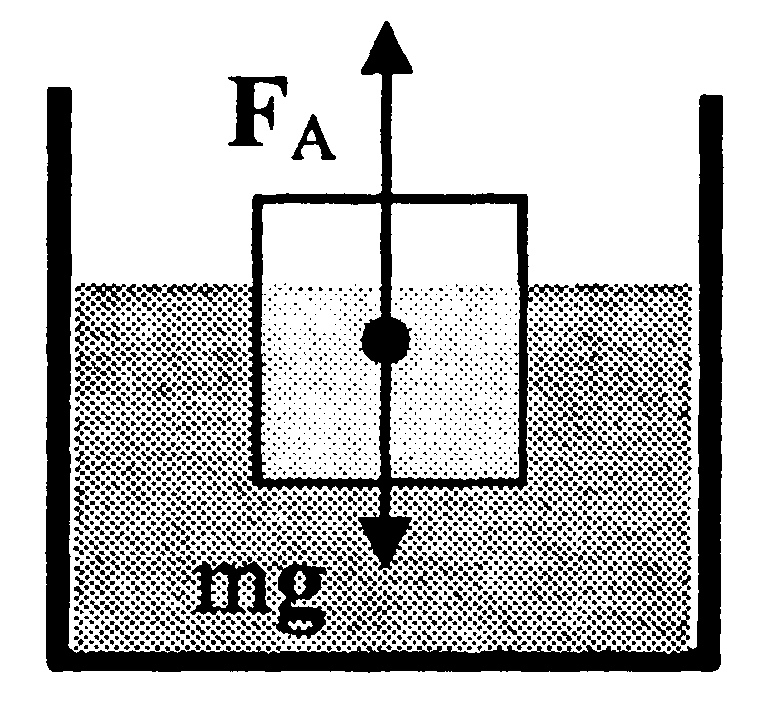
| ➨ на тело, погруженное в жидкость (газ), действует со стороны этой жидкости (газа) выталкивающа€ сила Fјрх, равна€ весу вытесненной телом жидкости (газа), направленна€ вертикально вверх и приложенна€ к центру т€жести вытесненного объема;
➨Vт Ц объем погруженной в жидкость части тела;
ρж Ц плотность жидкости;
| |
| | ● услови€
плавани€ тел
на поверхности
жидкости
| ➨Fјрх= mg Ц плавает - архимедова сила равна силе т€жести (тело может плавать на данной глубине бесконечно долго);
➨ Fјрх< mg Ц тонет Ц архимедова сила меньше силы т€жести (тело тонет и опускаетс€ на дно);
➨ Fјрх> mg Ц всплывает Ц архимедова сила больше силы т€жести (тело всплывает до тех пор, пока не начнет плавать).
| |
| | ƒ¬»∆≈Ќ»≈
∆»ƒ ќ—“»
ѕќ “–”Ѕјћ
| 
| |
| | |
| |
| | ● условие
несжимаемости
жидкости
| ➨ при переходе из одного сечени€ трубы  в другое в другое  несжимаема€ жидкость не измен€ет свой объем несжимаема€ жидкость не измен€ет свой объем
 или или  ( ( ) )
| |
| | ● стационарное
движение жидкости
(установившеес€)
| ➨ движение, при котором через любое поперечное сечение трубы за одинаковые промежутки времени t проходит один и тот же объем V жидкости
 или или  ( ( ) )
| |
| | ● уравнение
неразрывности
 или
или

| ➨ - при стационарном движении идеальной жидкости по трубе, в любой точке потока произведение скорости  движени€ жидкости на поперечное сечение движени€ жидкости на поперечное сечение  трубы есть величина посто€нна€; т.к. трубы есть величина посто€нна€; т.к.  ,следовательно,
● в узких част€х трубы Ц скорость движени€
жидкости больше;
● в широких част€х Ц скорость движени€
жидкости меньше; ,следовательно,
● в узких част€х трубы Ц скорость движени€
жидкости больше;
● в широких част€х Ц скорость движени€
жидкости меньше;
| |
| | ● идеальна€ жидкость
| ➨ жидкость, не имеюща€ структуры, непрерывна€ и несжимаема€, в которой отсутствует внутреннее трение;
➨ абстрактна€ модель реальной жидкости, которой можно пользоватьс€ на практике при малых скорост€х движени€ жидкости.
| |
| | «ависимость
давлени€ жидкости
от скорости
ее течени€
| ➨при стационарном течении жидкости в тех местах, где
скорость  течени€ жидкости меньше, давление р в жидкости больше и, наоборот; течени€ жидкости меньше, давление р в жидкости больше и, наоборот;
| 
| |
| | ● уравнение Ѕернулли
 =
= =
=  или
или
 =const =const
| ➨ полное давление жидкости, равно сумме:
динамического  ,
гидростатического ρgh,
статического
р
давлений и €вл€етс€ посто€нной величиной; ,
гидростатического ρgh,
статического
р
давлений и €вл€етс€ посто€нной величиной;
|  наклонна€ труба
наклонна€ труба
| |
| | ● уравнение Ѕернулли
(сокращенное)
 const const
| ➨ статическое давление р в потоке выше там, где меньше динамическое  давление, то есть скорость давление, то есть скорость  течени€ жидкости;. течени€ жидкости;.
|  горизонтальна€ труба
горизонтальна€ труба
| |
| | ● формула “орричелли

| ➨  - модуль скорости жидкости при вытекании из малого отверсти€ в сосуде;
➨ Ќ Ц высота столба жидкости над отверстием. - модуль скорости жидкости при вытекании из малого отверсти€ в сосуде;
➨ Ќ Ц высота столба жидкости над отверстием.
|
| |
| | | | | | | | | | | | | | | | | | | | | |


 =
=6,67∙10-11
=
=6,67∙10-11 
 =mg
=mg


 (на разных планетах разное);
3) g зависит от квадрата радиуса «емли
(на разных планетах разное);
3) g зависит от квадрата радиуса «емли  ;
● на экваторе gЁ= 9,78 м/с2;
● на полюсе gѕ= 9,83 м/с2;
● на широте
;
● на экваторе gЁ= 9,78 м/с2;
● на полюсе gѕ= 9,83 м/с2;
● на широте  g = 9,80 м/с2;
g = 9,80 м/с2;
 ¬≈— “≈Ћј
¬≈— “≈Ћј
 [H]
[H]
 ¬ес тела, движущегос€ с ускорением
¬ес тела, движущегос€ с ускорением


 км/с
км/с
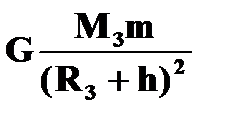 =
= 
 , т.к. h=0,
, т.к. h=0,  , то
, то 


 11,2 км/с
11,2 км/с
 или
σ = ε∙ Ε
или
σ = ε∙ Ε


 пропорционально относительному удлинению
пропорционально относительному удлинению  ;
;

 [ѕа]
[ѕа]

 «а точкой D происходит разрушение тела.
«а точкой D происходит разрушение тела.


 поко€ >
поко€ >  скольжени€;
▪
скольжени€;
▪  >
>  ▪
▪  зависит от рода и шероховатости трущихс€ поверхностей; безразмерна€ величина;
зависит от рода и шероховатости трущихс€ поверхностей; безразмерна€ величина;

 жидкостного зависит от площади поперечного сечени€ и формы тела;
▪
жидкостного зависит от площади поперечного сечени€ и формы тела;
▪  скольжени€ >
скольжени€ >  жидкостного.
жидкостного.
 >
>  );
▪ устанавливают шариковые и роликовые подшипники, т.е. замен€ют трение скольжени€ трением качени€ (
);
▪ устанавливают шариковые и роликовые подшипники, т.е. замен€ют трение скольжени€ трением качени€ ( )
)
 ƒвижение тела с учетом силы трени€
ƒвижение тела с учетом силы трени€
 N=mg;
Fтр=
N=mg;
Fтр=  N=
N=  mg
mg

 ;
;
 -Fтр
OY:0=N-mgcos
-Fтр
OY:0=N-mgcos 
 N=mg cos
N=mg cos  ;
Fтр=
;
Fтр=  N=
N=  mg cos
mg cos 
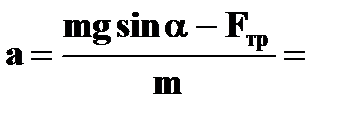 =
=  = g(sin
= g(sin  -
-  );
);

 =
= 





 –акета
–акета


 , отсюда
, отсюда



 / ћр
«нак Ђ‒ї показывает, что направление скорости ракеты противоположно направлению скорости вылетающих газов.
—корость ракеты
можно увеличить двум€ способами:
1) увеличить скорость
/ ћр
«нак Ђ‒ї показывает, что направление скорости ракеты противоположно направлению скорости вылетающих газов.
—корость ракеты
можно увеличить двум€ способами:
1) увеличить скорость  газов, вытекающих из сопла ракеты;
2) увеличить массу сгораемого топлива
газов, вытекающих из сопла ракеты;
2) увеличить массу сгораемого топлива  , что приводит к уменьшению полезной нагрузки Ц массы груза ракеты.
, что приводит к уменьшению полезной нагрузки Ц массы груза ракеты.
 ј=FЈS cos α
ј=FЈS cos α
 и перемещени€
и перемещени€  , умноженному на косинус угла
, умноженному на косинус угла  между этими векторами;
между этими векторами;


 - работа положительна€
- работа положительна€


 - работа равна нулю
- работа равна нулю

 ,
,  - работа отрицательна€
- работа отрицательна€
 =
= 
 ➨ равна произведению силы т€жести на разность высот в начальном
➨ равна произведению силы т€жести на разность высот в начальном  и конечном
и конечном  положени€х тела;
➨ не зависит от длины и формы пути, пройденного телом;
положени€х тела;
➨ не зависит от длины и формы пути, пройденного телом;




 < 0, т.к. направлени€ векторов силы и перемещени€ противоположны.
< 0, т.к. направлени€ векторов силы и перемещени€ противоположны.
 [¬т]
[¬т]
 [ƒж]
[ƒж]




 уравновесить большую силу
уравновесить большую силу  ;
;


 ● подвижный блок➨ дает выигрыш в силе в два раза
● подвижный блок➨ дает выигрыш в силе в два раза




 [%]
[%]


 [ѕа]
[ѕа]
 )
Ј гидростатическое давление
р=ρgh
)
Ј гидростатическое давление
р=ρgh


 ,
наход€щихс€ в сообщающихс€ сосудах, обратно пропорциональны плотност€м этих жидкостей
,
наход€щихс€ в сообщающихс€ сосудах, обратно пропорциональны плотност€м этих жидкостей



 - гидравлический пресс дает выигрыш в силе, но проигрыш в длине пути поршн€;
●
- гидравлический пресс дает выигрыш в силе, но проигрыш в длине пути поршн€;
●  - силы, действующие на поршни пропорциональны площад€м этих поршней;
- силы, действующие на поршни пропорциональны площад€м этих поршней;


 в другое
в другое  несжимаема€ жидкость не измен€ет свой объем
несжимаема€ жидкость не измен€ет свой объем
 или
или  (
( )
)
 или
или  (
( )
)
 или
или

 движени€ жидкости на поперечное сечение
движени€ жидкости на поперечное сечение  трубы есть величина посто€нна€; т.к.
трубы есть величина посто€нна€; т.к.  ,следовательно,
● в узких част€х трубы Ц скорость движени€
жидкости больше;
● в широких част€х Ц скорость движени€
жидкости меньше;
,следовательно,
● в узких част€х трубы Ц скорость движени€
жидкости больше;
● в широких част€х Ц скорость движени€
жидкости меньше;
 течени€ жидкости меньше, давление р в жидкости больше и, наоборот;
течени€ жидкости меньше, давление р в жидкости больше и, наоборот;

 =
=
=
=  или
или
 =const
=const
 ,
гидростатического ρgh,
статического
р
давлений и €вл€етс€ посто€нной величиной;
,
гидростатического ρgh,
статического
р
давлений и €вл€етс€ посто€нной величиной;
 наклонна€ труба
наклонна€ труба
 const
const
 давление, то есть скорость
давление, то есть скорость  течени€ жидкости;.
течени€ жидкости;.
 горизонтальна€ труба
горизонтальна€ труба

 - модуль скорости жидкости при вытекании из малого отверсти€ в сосуде;
➨ Ќ Ц высота столба жидкости над отверстием.
- модуль скорости жидкости при вытекании из малого отверсти€ в сосуде;
➨ Ќ Ц высота столба жидкости над отверстием.






 - длина стержн€ в неподвижной системе отсчета, отно-сительно которой стержень покоитс€;
- длина стержн€ в неподвижной системе отсчета, отно-сительно которой стержень покоитс€;
 - длина стержн€ в подвижной системе отсчета, относи-тельно которой стержень движетс€ со скоростью
- длина стержн€ в подвижной системе отсчета, относи-тельно которой стержень движетс€ со скоростью  .
—окращение длины тем больше, чем больше скорость движени€.
ѕоперечные размеры тела не завис€т от скорости его движени€ и одинаковы во всех инерциальных системах отсчета.
.
—окращение длины тем больше, чем больше скорость движени€.
ѕоперечные размеры тела не завис€т от скорости его движени€ и одинаковы во всех инерциальных системах отсчета.

 - интервал времени между двум€ событи€ми, происход€-щими в одной и той же точке неподвижной системы отсчета;
➨
- интервал времени между двум€ событи€ми, происход€-щими в одной и той же точке неподвижной системы отсчета;
➨  - интервал между этими же событи€ми в подвижной системе отсчета, движущейс€ относительно неподвижной со скоростью
- интервал между этими же событи€ми в подвижной системе отсчета, движущейс€ относительно неподвижной со скоростью 
 - подвижна€ система отсчета, котора€ движетс€ со скоростью
- подвижна€ система отсчета, котора€ движетс€ со скоростью  вдоль оси ќ’ относительно неподвижной системы отсчета .
➨точкаћдвижетс€ со скоростью
вдоль оси ќ’ относительно неподвижной системы отсчета .
➨точкаћдвижетс€ со скоростью  вдоль оси
вдоль оси  подвижной системы
подвижной системы 

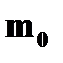 - масса поко€щегос€ тела; масса поко€ €вл€етс€ величиной, одинаковой дл€ всех систем отсчета, в которых тело покоитс€.
➨
- масса поко€щегос€ тела; масса поко€ €вл€етс€ величиной, одинаковой дл€ всех систем отсчета, в которых тело покоитс€.
➨  - масса того же тела, но движущегос€ со скоростью
- масса того же тела, но движущегос€ со скоростью  возрастает.
возрастает.

 , приложенной к материальной точке (телу), равен изменению вектора рел€тивистского импульса
, приложенной к материальной точке (телу), равен изменению вектора рел€тивистского импульса  тела (или материальной точки) за единицу времени
тела (или материальной точки) за единицу времени



 и энергией поко€
и энергией поко€  .
.

