Определение вероятной ошибки результата

 

Иногда при статистической обработке результатов изме­рений используют вероятную ошибку наблюдений и вероят­ную ошибку результата.

Все ошибки наблюдения (измерения) заключаются между наибольшими по абсолютной величине положительными и отрицательными значениями абсолютных ошибок 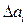, причем большие случайные ошибки в ту или другую сторо­ну реже встречаются и менее вероятны, чем малые. Поэто­му есть основание сузить пределы погрешностей, определяе­мых по формулам для квадратичной ошибки отдельного из­мерения а и средней квадратичной ошибки результата m

 

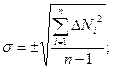
Для этого вводят некоторый коэффициент, меньший 1 и равный по теории вероятностей 0,67 (точнее, 0,6745). Таким образом, вероятная ошибка отдельного наблюдения f (от французского faufe – ошибка) будет равна:

 

, если n <30, (16)

и

 

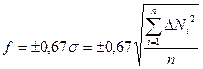, если n 30. (17)

 

Вероятная ошибка F будет

, если n <30, (18)

 

, если n 30, (19)

 

 

Таким образом, для окончательного значения измеряе­мой величины А можно написать:

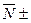= 0,67 m или = 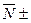0,67 (20)

где — среднее арифметическое, которое определяет собой наиболее вероятное значение измеряемой величи­ны;

±0,67 – величина вероятной ошибки результата измерений.

Определим вероятную ошибку результата измерений в примере 2:

 

0,67 m = 0,67·2,52=1,69;

0,67 m_ф = 0,67·1=0,67;

 

или

0,67 m₀ =0,67 2,71 = 1,82.

 

Ответ: = 135,00+1,82 имп/мин.

 

Значит, вероятнее всего, что значение истинной скорости счета будет находиться в интервале от (135–1,82) до (135+1,82) имп/мин или при округлении результата от 133 до 137 имп/мин.