Ошибки результата

Обработку полученных результатов можно провести, используя понятие средней квадратичной ошибки результата, устанавливаемое теорией вероятности. Рассмотрим последовательный ход анализа для нахождения средней квадратичной ошибки результата.

Пусть имеется ряд измерений 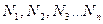. Определим среднее арифметическое , используя формулу (1), и абсолютные ошибки отдельных измерений по формуле (2). Далее необходимо найти квадраты отклонений и сумму квадратов отклонений . Все это представим в виде табл. 1.

Таблица 1. Результаты измерений

Индекс измерения i	результат измерений _i	Абсолютная ошибка отдельных измерений	Квадрат отклонений
… n_i	_……….	...	…
n =

Величина квадратичного отклонения, приходящаяся на одно измерение, называется дисперсией и определяется по формуле

, (7)

откуда величина среднего квадратичного отклонения

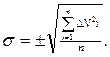(8)

Если число измерений n меньше 30 (n <30), то

(9)

Значение σ часто называют средней квадратичной ошибкой отдельного измерения или стандартным отклонением.

Средней квадратичной ошибкой результата по теории вероятностей называется стандартное отклонение, деленное на корень квадратный из числа наблюдений:

, (10)

или

. (11)

Если n <30, то

. (12)

Таким образом, истинное значение измеряемой величины

или . (13)

Из этой формулы видно, что чем больше число измерений n, тем меньше величина средней квадратичной ошибки результата m.

Отметим, что определять ошибку результата, пользуясь средней квадратичной ошибкой результата m, более целесообразно, чем определять относительную ошибку результата (6), но само вычисление оказывается несколько более громоздким.

Если провести исследование частоты распределения значений измеряемой величины около среднего арифметического значения , то получается, что при отклонении от значения среднего арифметического в пределах 1 σ располагается 68,3% значений измеряемой величины, в пределах 2 σ – 95,5, в пределах 3 σ – 99,7%.

Обычно это представляют графически и называют нормальной кривой распределения Гаусса значений измеряемой величины (прилож. 2).

Значение определяет собой величину среднего арифметического. По обе стороны от располагаются значения с недостатком и с избытком, отклоняющиеся от значения на величину 1 σ, 2 σ и 3 σ. Из графика видно, что значения, расположенные близко к среднему арифметическому , встречаются наиболее часто: на участке, ограниченном в пределах +σ и -σ, располагается 68,3% всех значений; в зоне +2σ и -2σ располагается уже 95,5% значений и, наконец, на участке в пределах от + 3 σ и - 3 σ располагается уже 99,7% значений.

Знание этого закона, распределения значений измеряемой величины бывает полезно при определении принадлежности измеренного значения, которое может отличаться от всех остальных измеренных значений, к данным измерениям. Этот вопрос решается следующим образом. Определяется квадратичное отклонение а и, если величина абсолютной ошибки данного измерения лежит в пределах значения утроенной квадратичной ошибки отдельного наблюдения , то значение должно быть принято в расчет. Если же , то такое измерение после повторного тщательного исследования необходимо отбросить. Для овладения практикой расчетов приведем пример.

Пример (2) При определении активности радиоактивного образца получены значения скорости счета: 190, 179, 175, 187, 170, 174, 169, 191, 181, 175 имп/мин. Показатели скорости счета фона соответственно составляли 46, 39, 47, 45, 49, 39, 38, 45, 42, 40, 47, 44, 46, 39, 49 импульсов в минуту.

Решение. Обработка данных производится в три этапа:

1. Последовательно определяем среднее арифметическое для фона , абсолютные ошибки отдельных измерений , значение квадратов отклонений ; значение средней квадратичной ошибки отдельного отклонения 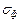, значение средней квадратичной ошибки результата , величину .

2. Аналогичные расчеты проводим при определении скорости счета образца с учетом фона.

3. Находим истинную скорость счета образца, для чего из значения скорости счета с учетом фона вычтем значение фона , т. е. .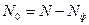

Начнем обработку результатов:

1. Определим значения фона. Для удобства расчеты сведем в табл. 2.

Таблица 2. Результаты измерений скорости счета фона

Индекс измерения i	Результат измерения , имп/мин	Абсолютная ошибка измерения , имп/мин	Квадрат отклонения
		+2
		-5
		+3
		+ 1
		+5
		-5
		-6
		+ 1
		-2
		-4
		+3

		+2
		-5
		+5
n=15

Так как 15<30, то

Проверим, все ли значения относятся к нашему ряду. Для этого определим 3 σ_ф и сравним с ним отклонения всех измерений:

Все значения , то есть меньше 3 σ_ф. Следовательно, все значения относятся к нашему ряду и должны учитываться.

Определим среднюю квадратичную ошибку результата:

Итак, имп/мин.

Найдем относительную ошибку результата измерений:

44 имп/мин — 100%

1 имп/мин — х.

Отсюда .

Эта точность измерения нас удовлетворяет.

2. Определим скорость счета образца с учетом фона. Расчеты сведем в табл. 3.

Таблица 3. Результаты измерений скорости счета образца+фон

Индекс измерения i	Результат измерения , имп/мин	Абсолютная ошибка измерения, , имп/мин	Квадрат отклонений

		+ 11

		– 4
		+8
		– 9
		– 5
		–10
		+ 12
		+2
		– 4
n=10

Так как 10<30, то

Проверим, все ли значения будем учитывать:

Как видно, <23,9. Тогда

Итак, .

Относительная ошибка будет:

179 имп/мин — 100%

2,52 имп/мин — х.

Отсюда .

Эта точность измерения нас вполне удовлетворяет.

3. Теперь найдем истинную скорость счета образца. Совершенно естественно, что истинная скорость счета образца равна скорости счета образца+фон () минус скорость счета фона (), которые соответственно равны:

и .

Что касается ошибки результата при определении собственной скорости счета образца, то в ней должны быть учтены и средняя квадратичная ошибка результата, полученная при измерении скорости счета образца+фон, то есть m, и средняя квадратичная ошибка результата, полученная при измерении скорости счета фона, то есть m_ф _.

Согласно теории вероятностей, средняя квадратичная ошибка равна корню квадратному из суммы квадратов отдельных ошибок, то есть

. (14)

Тогда собственная скорость счета образца будет равна

. (15)

Подставим числовые данные:

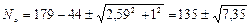=135±2,71,

то есть

имп/мин.

Относительная ошибка будет:

135 имп/мин — 100%

2,71 имп/мин — х.

Отсюда

Данная точность измерения собственной активности излучения образца является вполне достаточной.

Рассмотренный пример показывает, что нахождение средней квадратичной ошибки результата измерений по способу наименьших квадратов является простым, но связан с длительными вычислениями. Этот способ требует n измерений, что при определении активности препарата радиоактивного вещества связано с рядом неудобств. Помимо того, что для фиксирования результатов отдельных наблюдений (например, каждую минуту, 5 раз по 3 минуты, даже 3 раза по 5 минут) требуется много труда, возникает возможность большой ошибки на просчет при проведении отдельных измерений. Гораздо рациональнее измерять активность препарата длительное время, непрерывно, что практически и делается.