1.1. Событием (U) называют всякий факт, который может произойти или не произойти.
1.2. Вероятностью события P(U) называется численная мера степени объективной возможности этого события.
1.3. Достоверным событием называют событие (U), которое в результате опыта непременно должно произойти. Вероятность достоверного события принимается равной единице, т.е. P(U) = 1.
1.4 Невозможным событием называют событие Q, которое в результате опыта никоим образом не может произойти. Вероятность невозможного события принимается равной нулю, т.е. P(Q)=0.
1.5 Из п.1.3. и 1.4. следует, что вероятность любого реального события (А) заключена в интервале от 0 до 1, т.е. 
.
1.6 Несколько событий в данном опыте называют несовместными, если никакие два из них не могут произойти одновременно.
1.7.Несколько событий в данном опыте называют равновозможными, если по условиям симметрии опыта нет оснований считать какое-либо из них более предпочтительным или возможным.
1.8. Условной вероятность события А при наличии события В называют вероятность события А, вычисленную при условии, что событие В произошло. Условная вероятность в этом случае обозначается как Р(А/В).
1.9.События называются независимыми, если появление одного из них никоим образом не меняет вероятности появления другого. Для независимых событий А и В справедливо:
, 
.
1.10. Полной группой событий называют несколько событий таких, что в результате опыта непременно произойдет хотя бы одно из них. Если события Аk (k=1, 2, …,n) составляют полную группу событий и несовместны, то
,
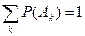так как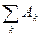 
- достоверное событие.
1.11. Если несколько событий
а) образуют полную группу событий;
б) несовместны;
в) равновозможны,
то вероятность события А можно вычислить по формуле
,
где n – общее число возможных событий (исходов опыта),
m – число событий, благоприятствующих событию А.
