Для практического использования понятия информации необходимо научиться ее измерять. Это можно сделать по аналогии с методикой численного измерения иных фундаментальных понятий, таких как материя (масса), энергия или пространство, для этого требуется установить, что принимается за меру количественной оценки информации и что принимать за единицу измерения этой меры. Под мерой количественной оценки понимают некоторое явление или объект, которые однозначно (пропорционально) связаны с определяемым первичным понятием и которые могут характеризовать количественное содержание этого понятия.
Таблица 1.1 иллюстрирует общепринятую методику измерения первичных понятий, таких как масса, пространство и т. п.
Таблица 1.1
| Первичное понятие. | Мера количественной оценки. | Ед. измер. меры кол. оценки. |
| Материя. | Вес. | Грамм, тонна и т.д. |
| Пространство. | Расстояние. | Метр, километр и т.д. |
| Информация | ? | ? |
Традиционно сложилось три основных подхода к выбору меры количественной оценки информации.
1. Структурный подход, при котором количественная оценка информации о событии оценивается путем определения объективной возможности этого события, входящего в некоторую полную группу событий.
2. Статистический подход, при котором количественная оценка информации о принятом сообщении производится на основе меры неопределенности, снимаемой с исследуемого информационного процесса (события) при получении данного сообщения.
3. Семантический подход, который в основном учитывает ценность полученной информации с точки зрения конкретного получателя этой информации.
Очевидно, что, для точного, технического, объективного использования, семантический подход не приемлем, так как он сугубо субъективен и не может дать общепринятой количественной меры информации, хотя этот подход и может быть использован в сфере гуманитарных и общественных наук.
Применительно к точным и техническим наукам для определения меры количественной оценки информации используют структурный и статистический подходы.
Выбор критерия для количественной оценки информации, независимо от выбранного полхода, должен удовлетворять условиям, вытекающим из практического опыта:
— сообщению большей длины (при одном и том же объеме алфавита) соответствует большее количество информации;
— большее количество информации содержится в тех сообщениях (одинаковой длины), которые составлены из символов большего алфавита;
— символы в сообщении могут появляться с различными вероятностями и могут быть статистически зависимыми.
Учитывая это, меру количественной оценки информации можно ввести исходя из следующих соображений. Предположим, что какое-то событие имеет m равновероятных исходов, например, появление какого-либо символа из алфавита, содержащего m таких символов. Измерить количество информации, содержащееся в сообщении из n таких символов можно, определив число N всех возможных сообщений, которые могут быть составлены из символов этого алфавита. Если сообщение формируется из одного символа, то 
N=m, если из двух, то 
, если из n символов, то 
. Полученную меру количественной оценки информации можно понимать как меру неопределенности получения конкретного заданного сообщения, состоящего из n символов алфавита. Однако эта мера количественной оценки информации не совсем удобна. Действительно, при 
(т.е. алфавит состоит из одного символа) неопределенности не существует и появление этого символа не несет никакой информации, однако значение N в этом случае (N=1n) не обращается в нуль. Кроме этого, из практических соображений, целесообразно считать, что количество информации, полученное от двух независимых источников, равно сумме количеств информации, получаемых от каждого источника, а предлагаемая мера количества информации дает в этом случае произведение 
, где 
— число возможных сообщений от двух источников сообщений. Эти неудобства легко преодолимы, если в качестве меры количественной оценки информации (
) взять логарифм по какому-либо основанию от общего числа возможных сообщений 
(1.1)
или логарифм вероятности появления конкретного сообщения (Р)
(1.2)
при условии, что все сообщения равновероятны, т.е.
.
Определенная по формулам (1.1) и (1.2) мера количественной оценки информации (I) называется количеством информации. Количество информации как мера количественной оценки информации может быть вписана в соответствующую графу таблицы 1.1.
В случае если сообщения не равновероятны, мера неопределенности будет зависеть не только от общего числа возможных сообщений, но и от распределения вероятности между возможными сообщениями.
В общем случае, при наличии шумов, понятие количества информации может быть определено из следующих соображений.
Если поступило сообщение о событии, априорная вероятность, которого равна 
характеризует состояние системы до получения сообщения, т.е. до опыта), а после приема сообщения апостериорная вероятность этого события стала для получателя 
( характеризует состояние системы после получения сообщения), то прирост количества информации (I), связанный с приемом сообщения о событии, определяется выражением
. (1.3)
Это выражение часто называют основным соотношением теории информации.
В частном случае, когда шумы при передаче и приеме сообщения отсутствуют, событие после приема сообщения о нем становится достоверным, т.е.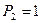 
и выражение (1.3) принимает вид:
. (1.4)
Таким образом, количество информации, содержащееся в сообщении, зависит от вероятности события до приема сообщения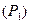 
, и чем меньше эта вероятность, т.е. чем больше неопределенность исхода, тем больше количество информации о нем получается в результате приема сообщения. Поскольку Р £ 1, то определяемое формулой (1.4) количество информации всегда положительно. Следовательно, приём какого-либо сообщения никоим образом не может уменьшить количество уже имеющейся информации.
Единицы измерения количества информации определяются выбором основания логарифмов в выражениях (1.1) - (1.4). Если основание логарифмов берется равным 2, то получаем единицу количества информации бит (от английского binary digit, - двоичное число). Таким образом, один бит это количество информации, получаемое при приеме одного из двух равновероятных символов сообщения.
Если основание логарифмов равно 10, то единица количества информации носит название дит, а если используются натуральные логарифмы (по основанию е) – то нат.
Использование выше указанных формул часто бывает затруднено, поэтому на их основе получают иные выражения для определения количества информации, которые более просты и практичны, однако применимы лишь к конкретным видам сообщений.
