Представляет интерес определение вида функции плотности распределения вероятности символов (p (x)) непрерывного сообщения х (t), с заданными пределами изменения символов, которая обращает энтропию этого непрерывного сообщения (Hx) в максимум.
Пусть непрерывное сообщение х (t) представляет собой ограниченную непрерывную функцию с областью значений из интервала [ а;b ] (Рис. 1.3) и с неизвестной плотностью распределения вероятностей символов p(x), которая удовлетворяет условию
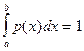. (1.17)
Рис. 1.3..График непрерывного сообщения х (t).
Поставим задачу найти распределение pmax(x), при котором дифференциальная энтропия этого сообщения
принимает максимальное значение.
Для решения этой задачи воспользуемся методом неопределенных множителей Лагранжа, который используется для нахождения локальных экстремумов функций нескольких переменных. Суть этого метода заключается в следующем. Если задана функция нескольких переменных, например 
, аргументы которой удовлетворяют некоему уравнению связи 
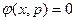, то можно составить функцию Лагранжа 
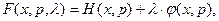
а локальные экстремумы определить из решения системы уравнений:
.
В данном случае функция 
имеет вид:
,
а уравнение связи получим из выражения (1.17).
Составив функцию Лагранжа
,
и продифференцировав ее по p (p не зависит от x, поэтому достаточно продифференцировать подынтегральное выражение), на основании необходимого условия существования экстремума получим:
.
Откуда после несложных преобразований
имеем:
при 
Подставив это выражение в (1.17) получим:
,
и используя предыдущее равенство находим:
, при .
Следовательно, искомая функция плотности распределения вероятности (pmax (x)) запишется в виде:
Таким образом, энтропия непрерывного сообщения принимает свое максимальное значение при равновероятном появлении всех символов, принадлежащих интервалу [а;b]. При этом максимально возможное значение энтропии будет определяться по формуле
.
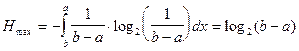