Приклад застосування двоїстого симплекс-методу

Приклад 6.1. Розв’яжемо ЗЛП двоїстим симплекс-методом:

min z = x ₁ + x ₂; (6.8)

; (6.9)

; (6.10 )

; (6.11)

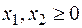. (6.12)

Зведемо спочатку всі обмеження до типу ”£”; для цього нерівності типу “³” помножимо на –1:

;

;

.

А тепер у кожне з них введемо відповідну залишкову змінну:

;

;

.

Ітерація 1. Початковий базисний розв’язок (недопустимий) задачі такий:

= .

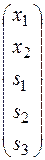На рис. 6.1 цей розв’язок відповідає точці А (0, 0).

Заповнюємо симплекс-таблицю (табл. 6.2).

Таблиця 6.2

Базисні змінні	x 1	x 2	s 1	s 2	s 3	Розв’язок
z	-1	-1
s 1	-2	-1				-4
s 2	-1	-2				-4
s 3

Значення залишкових змінних не забезпечують одержання допустимої стартової точки прямої задачі, але всі елементи z-рядка (d_j) є недодатними — умова оптимальної задачі на мінімізацію виконується.

Крок 1. Вибираємо змінну, що виводиться з множини базисних

За умовою допустимості за виводжувану з базису змінну вибирається най­більша за модулем від’ємна базисна змінна. Таких змінних дві: s ₁ = –4; s ₂ = –4.
У цьому випадку можна вибрати будь-яку змінну. Виберемо змінну s ₂.

Крок 2. Вибираємо змінну, що вводиться у множину базисних

За умовою оптимальності змінна, що вводиться у базис, вибирається з небазисних таким чином: обчислюються відношення коефіцієнтів лівої частини z-рів­няння до відповідних коефіцієнтів рівняння, яке відповідає виводжуваній змінній. Відношення з додатними або нульовими значеннями знаменника не враховуються. У задачі на мінімізацію змінній, що вводиться, повинне відповідати найменше з вказаних співвідношень (табл. 6.3). У задачі на максимізацію вибираємо відношення, найменше за абсолютною величиною:

Таблиця 6.3

Базисні змінні	x 1	x 2	s 1	s 2	s 3	Розв’язок
Z	-1	-1
s 2	-1	-2				-4
Відношення	1	1/2	—	—	—	—

Обчислюємо q = min{1,¹/₂} = ¹/₂, тобто вводимо до базису змінну x ₂.

Крок 3. Виконаємо операцію заміщення, використовуючи перетворення Жордана-Гаусса (тобто звичайні симплекс-перетворення) (табл. 6.4).

Таблиця 6.4

Базисні змінні	x 1	x 2	s 1	s 2	s 3	Розв’язок
z	-1/2			-1/2
s 1	-3/2			-1/2		-2
x 2	1/2			-1/2
s 3				1/2

Новий базисний розв’язок відповідає точці В (2, 0) (рис. 6.1).

Ітерація 2

Крок 1. Вибираємо змінну, що виводиться з множини базисних.

Розв’язок ще не допустимий (s ₁ = –2). За умовою допустимості за змінну, що виводиться з базису, вибираємо змінну s ₁.

Крок 2. Вибираємо змінну, що вводиться до базису (табл. 6.5).

Таблиця 6.5

Базисні змінні	x 1	x 2	s 1	s 2	s 3	Розв’язок
z	-1/2			-1/2
s 1	-3/2			-1/2		-2
x 2	-1			-1/2
s 3				1/2
Відношення	1/3	—	—		—

Обчислюємо q = min{¹/₃, 1} = ¹/₃, тобто вводимо до базису змінну x ₁.

Крок 3. Виконуємо операцію заміщення (табл. 6.6).

Таблиця 6.6

Базисні змінні	x 1	x 2	s 1	s 2	s 3	Розв’язок
z			-1/3	-1/3		8/3
x 1			-2/3	1/3		4/3
x 2			1/3	-2/3		4/3
s 3			1/3	1/3		22/3

Розв’язок, що є оптимальним і допустимим, відповідає точці С (⁴/ ₃, ⁴/ ₃ ).

Рис. 6.1