Розглянемо теоретичне обґрунтування методу [12].
Крок 1. Вибір змінної, що виводиться з множини базисних (умови допустимості)
За змінну, що виводиться з базису, треба вибрати найбільшу за абсолютною величиною від’ємну базисну змінну, тобто вибрати ведучий рядок q, такий, що
.
Якщо всі базисні змінні ³ 0 (тобто такого q не існує), то СТОП, одержали допустимий і оптимальний розв’язок. У протилежному випадку стовпчик, що відповідає змінній 
, повинен бути виведений з базису.
Крок 2. Вибір змінної, що вводиться в множину базисних (умова оптимальності)
Якщо j-й небазисний стовпчик замінює q-й базисний, тоді після застосування перетворень Гаусса відносна оцінка q-го стовпчика в новому ДБР буде дорівнювати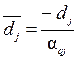 
. Для того, щоб компоненти вектора d N, як і раніше, були невід’ємні (виконувалась умова оптимальності), знаменник повинен бути від’ємним.
Визначимо коефіцієнт q за формулою
(6.7)
і нехай мінімум досягається при j = p.
Якщо у q -му рядку немає жодного 
для j, які відповідають небазисним змінним (ознака відсутності допустимих розв’язків), то СТОП, пряма задача не має допустимих розв’язків.
Отже, у множину базисних будемо вводити змінну 
:
;
.
Якщо взяти більше значення параметра q, ніж те, яке дає (6.7), наприклад значення, яке відповідає j = r, і якщо змінну 
ввести в базис, то в новому розв’язку одержимо
, тому що 
і умови оптимальності ДБР прямої задачі не будуть виконуватися.
Крок 3. Перехід до нового ДБР
За допомогою елементарних перетворень Гауcса виконується операція заміщення на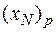 
. Перехід до кроку 1.
Схема двоїстого симплекс-методу для задачі мінімізації ЦФ відрізняється від схеми розв’язання задачі на максимум у правилі вибору змінної, що виводиться (критерії оптимальності).
Коефіцієнт q визначають за формулою
(6.7а)
(як і раніше розглядаються тільки відношення з від’ємним знаменником).
Ознака відсутності допустимих розв’язків така сама: у рядку, що відповідає вивідній змінній, немає жодного 
для j, які відповідають небазисним змінним.
З урахуванням (6.7) і (6.7а) можна записати єдине (для задач максимізації та мінімізації) правило вибору ведучого стовпчика:
.
Таким чином, двоїстий симплекс-метод на кожному кроці забезпечує умову оптимальності розв’язку і систематичне наближення його до області допустимих розв’язків. Коли отриманий розв’язок виявляється допустимим, ітераційний процес обчислень закінчується, оскільки цей розв’язок є і оптимальним.
У табл. 6.1 наведено порівняльну характеристику прямого і двоїстого симплекс-методів.
Таблиця 6.1
| Прямий симплекс-метод | Двоїстий симплекс-метод | |
| Проміжний розв’язок | Задача на мінімізацію " хj ³ 0 і $ j dj > 0. Проміжні розв’язки є допустимими, але неоптимальними за критерієм оптимальності | Задача на максимізацію " dj ³ 0, але $ j xj < 0. Проміжні розв’язки є оптимальними за критерієм оптимальності, але не є допустимими |
| Проміжний розв’язок | Задача на максимізацію " хj ³ 0 і $ j dj < 0. Проміжні розв’язки є допустимими, але не є оптимальними. | Задача на мінімізацію " dj £ 0, але $ j xj < 0. Розв’язки є оптимальними за критерієм оптимальності, але не є допустимими. |
| Опти-мальний розв’язок | Задача на мінімізацію | |
| " xj ³ 0 " dj £ 0 | " xj ³ 0 " dj £ 0 |
Продовження таблиці 6.1
| Задача на максимізацію | |||
| " xj ³ 0 " dj ³ 0 | " xj ³ 0 " dj ³ 0 | ||
| Етапи методу | 1. Умова оптимальності. Вибір змінної, що вводиться у базис: вводимо ту змінну xj у якій dj > 0 (min); dj < 0 (max). 2. Умова допустимості. Вибір змінної, що виводиться з базису: вибираємо змінну таким чином, щоб зберегти допустимість розв’язку, що отримується | 1. Умова допустимості. Вибір змінної, що виводиться з базису: виводимо ту змінну x j, для якої виконується: xj < 0. 2. Умова оптимальності. Вибір змінної, що вводиться в базис: вибираємо змінну таким чином, щоб зберегти оптимальність розв’язку | |
