В практике измерений часто возникает необходимость проверки гипотезы при небольшом числе измерений. В этом случае используется ограниченный уровень значимости 0,02 ≤ q ≤ 0,1.
Эта гипотеза проверяется с помощью двух критериев.
Критерий 1. По данным наблюдений x1,x2 ,x3,...,xn определим значение параметра d по формуле
,
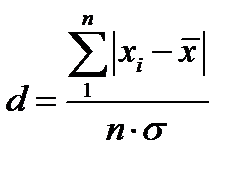где
.
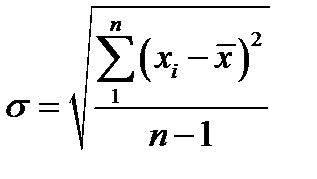Затем выбирают уровни значимости критерия q и по таблице 3.4 приложения 3 находят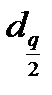 
и 
.
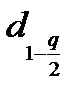Гипотеза о нормальности по критерию 1 не отвергается, если
.
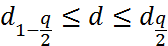
В противном случае гипотеза отвергается.
Критерий 2 (введен дополнительно для проверки "концов" распределений).
Пусть гипотеза о нормальности по критерию 2 не отвергается, если не более т разностей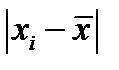 
превзошли 
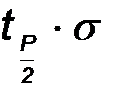, где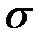 
вычисляется по формуле
,
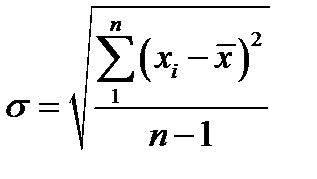а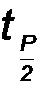 
- по таблицам нормированной функции Лапласа.
Значение p определяют по заданным n, q, m= 1 или 2 (составлена таблица 3.5 приложения 3). При 10 < n < 20 следует принимать m =1, а при 50 > n > 20 следует принимать m =2.
Если число разностей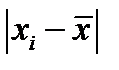 
, больших 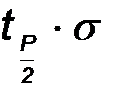превышает m, то гипотеза о нормальности отвергается.
Гипотеза о нормальности по составному критерию принимается, если для проверяемой группы данных выполняются оба критерия.
Вопрос №2
Оценивание погрешности косвенных измерений.
