Критерий согласия 
(критерий Пирсона)
Идея критерия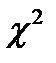 
состоит в контроле отклонений гистограммы экспериментальных данных от гистограммы с таким же числом интервалов, построенной на основе нормального распределения. Сумма квадратов разностей частот по интервалам не должна превышать значений 
, для которых составлены таблицы (приложение 3, таблица 3.6) в зависимости от уровня значимости q = 1 - Р и числа степеней свободы k = l - 3, где l - число интервалов.
Схема вычислений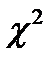 
:
1. Вычисляют среднее арифметическое значение результата измерений и среднее квадратичное отклонение по формулам:
,
.
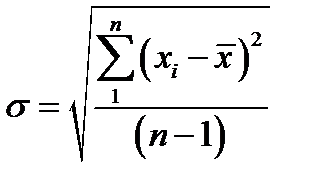2. Результаты измерений, в которых отсутствуют систематические погрешности, группируют по интервалам таким образом, чтобы эти интервалы покрывали всю ось (- ∞, + ∞) и чтобы количество данных в каждом интервале было достаточно большим (не менее 5).
3. Для каждого интервала 
подсчитывают число mi результатов измерения, попавших в этот интервал, а затем вычисляют вероятность Pi попадания в этот интервал при нормальном законе распределения, используя формулу Лапласа (табл. 3.7 приложения 3).
.
4. Если в какой-либо интервал теоретически попадает меньше пяти измерений, то его соединяют с соседним интервалом. Затем вычисляют показатель разности частот
,
где l - число всех интервалов (-∞,x), (x1,x2),..., (xl -1, ∞);
n - число измерений (n = m1+m2+m3+... +mn).
5. Выбирают уровень значимости критерия q. Он должен быть достаточно малым, чтобы была мала вероятность отклонить правильную гипотезу.
По уровню значимости q и числу степеней свободы k (таблица 3.6, приложения 3) находим границу критической области 
, так что
p{ 
> 
} = q.
Вероятность того, что получаемое значение превышает
, равна q
и мала.
Если оказывается, что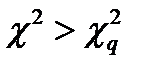 
, то гипотеза о нормальности отвергается.
Если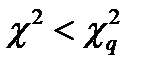 
, то гипотеза о нормальности принимается.
Чем меньше q, тем при том же k больше значение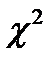 
, тем легче выполняется условие 
и принимается проверяемая гипотеза.
