Обработка результатов наблюдений
Вопрос №1
Прямые однократные и многократные измерения.
ПОРЯДОК ОБРАБОТКИ И ОЦЕНКИ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
Государственная система обеспечения единства измерений
ПРЯМЫЕ ИЗМЕРЕНИЯ С МНОГОКРАТНЫМИ НАБЛЮДЕНИЯМИ.
МЕТОДЫ ОБРАБОТКИ РЕЗУЛЬТАТОВ НАБЛЮДЕНИЙ
Основные положения
Настоящий стандарт распространяется на нормативно-техническую документацию, предусмотренную ГОСТ 8.010-72 и регламентирующую методику выполнения прямых измерений с многократными независимыми наблюдениями, и устанавливает основные положения методов обработки результатов наблюдений и оценивания погрешностей результатов измерений.
- Общие положения
a. При статической обработке группы результатов наблюдений следует выполнить следующие операции:
· исключить известные систематические погрешности из результатов наблюдений;
· вычислить среднее арифметическое исправленных результатов наблюдений, принимаемое за результат измерения;
· вычислить оценку среднего квадратического отклонения результата наблюдения;
· вычислить оценку среднего квадратического отклонения результата измерения;
· проверить гипотезу о том, что результаты наблюдений принадлежат нормальному распределению;
· вычислить доверительные границы случайной погрешности (случайной составляющей погрешности) результата измерения;
· вычислить границы неисключенной систематической погрешности (неисключенных остатков систематической погрешности) результата измерений;
· вычислить доверительные границы погрешности результата измерения.
Проверку гипотезы о том, что результаты наблюдений принадлежат нормальному распределению, следует проводить с уровнем значимости q от 10 до 2%. Конкретные значения уровней значимости должны быть указаны в конкретной методике выполнения измерений.
Для определения доверительных границ погрешности результата измерения доверительную вероятность P принимают равной 0,95.
В тех случаях, когда измерение нельзя повторить, помимо границ, соответствующих доверительной вероятности P=0,95, допускается указывать границы для доверительной вероятности P=0,99.
В особых случаях, например при измерениях, результаты которых имеют значение для здоровья людей, допускается вместо P=0,99 принимать более высокую доверительную вероятность.
- Результат измерения и оценка его среднего квадратического отклонения
2.1. Способы обнаружения грубых погрешностей должны быть указаны в методике выполнения измерений.
Если результаты наблюдений можно считать принадлежащими к нармальному распределению, грубые погрешности исключают в соответствии с указаниями в ГОСТ 11.002-73.
2.2. За результат измерения принимают среднее арифметическое результатов наблюдений, а которые предварительно введены поправки для исключения систематической погрешности.
Примечание: Если во всех результатов наблюдений содержится постоянная систематическая погрешность, допускается исключать ее после вычисления среднего арифметического неисправленных результатов наблюдений.
2.3. Среднее квадратическое отклонение результата наблюдения оценивают согласно разд. 1 ГОСТ 11.004-74.
2.4. Средне квадратическое отклонение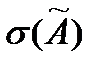 
результата измерения оценивается по формуле:
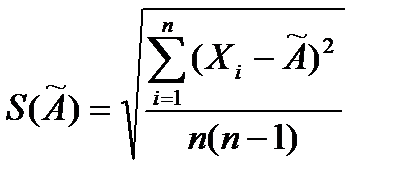
где: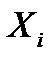 
- i-ый результат наблюдения;
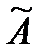- результат измерения (среднее арифметическое исправленных результатов наблюдений);
n - число результатов наблюдений;
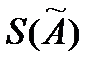- оценка среднего квадратического отклонения результата измерения.
- Доверительные границы случайной погрешности результата измерения
a. Доверительные границы случайной погрешности результата измерения в соответствии с настоящим стандартом устанавливают для результатов наблюдений, принадлежащих нормальному распределению.
Если это условие не выполняется, методы вычисления доверительных границ случайной погрешности должны быть указаны в методике выполнения конкретных измерений.
3.1.1 При числе результатов наблюдений n>50 для проверки принадлежности их к нормальному распределению по ГОСТ 11.006-74 предпочтительным является один из критериев: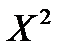 
Пирсона или 
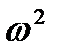Мизеса-Смирнова.
3.1.2. При числе результатов наблюдений 50>n>15 для проверки принадлежности их к нормальному распределению не проверяются. При этом нахождение доверительных границ случайной погрешности результата измерения по методике, предусмотренной настоящим стандартом, возможно в том случае, если заранее известно, что результаты наблюдений принадлежат нормальному распределению.
3.2. Доверительные границы e (без учета знака) случайной погрешности результата измерения находят по формуле:
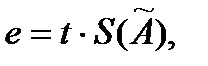
где t - коэффициент Стьюдента, который в зависимости от доверительной вероятности P и числа результатов наблюдений n находят по таблице справочного приложения 2.
- Доверительные границы неисключенной систематической погрешности результата измерения
a. Неисключенная систематическая погрешность результата образуется из составляющих, в качестве которых могут быть исключенные систематические погрешности:
· метода;
· средства измерений;
· вызванные другими источниками.
В качестве границ составляющих неисключенной систематической погрешности принимают, например, пределы допускаемых основных и дополнительных погрешностей средств измерений, ее случайные составляющие погрешности пренебрежимо малы.
4.2. При суммировании составляющих неисключенной систематической погрешности результата измерения неисключенные систематические погрешности средств измерений каждого типа и погрешности поправок рассматривают как случайные величины. При отсутствии данных о виде распределения случайных величин их распределения принимают за равномерные.
4.3. Границы неисключенной систематической погрешности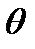 
результата измерения вычисляют путем построения композиции неисключенных систематических погрешностей средств измерений, метода и погрешностей, вызванных другими источниками. При равномерном распределении неисключенных систематических погрешностей эти границы (без учета знака) можно вычислить по формуле:
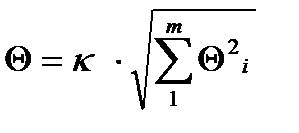
где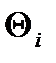 
- граница i-й неисключенной систематической погрешности;
k- коэффициент определяемый принятой доверительной вероятностью. Коэффициент k принимают равным 1,1 при доверительной вероятности P=0,95.
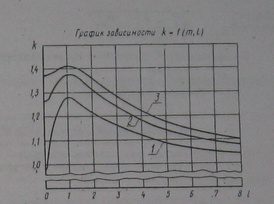
При доверительной вероятности P=0,99 коэффициент k принимают равным 1,4, если число суммируемых неисключенных систематических погрешностей равно четырем или менее четырех (
), то коэффициент k определяют по графику зависимости(см. чертеж)
k=f(m,l)
где: m – число суммируемых погрешностей;
;
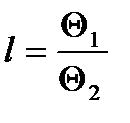кривая l - m=2;
кривая 2 - m=3;
кривая 3 - m=4.
При трех или четерех слагаемых в качестве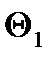 
принимают составляющую, по числовому значению наиболее отличающуюся от других, в качестве 
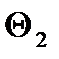следует принять ближайшую к 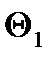составляющую.
Доверительную вероятность для вычисления границ неисключенной систематической погрешности принимают той же, что при вычислении доверительных границ случайной погрешности результата измерения.
- Граница погрешности результата измерения
5.1. В случае, если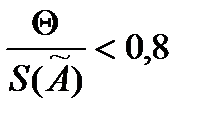 
, то неисключенными систематическими погрешностями по сравнению со случайными пренебригают и принимают, что граница погрешности результата 
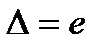. Если 
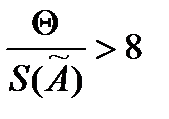, то случайной погрешностью по сравнению с систематическими пренебрегают и принимают, что граница погрешности результата измерения 
.
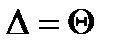Примечание. Погрешность, возникающая из-за пренебрежения одной из составляющих погрешности результата измерения при выполнении указанных неравенств, не превышает 15%.
5.2. В случае, если неравенства п. 5.1 не выполняются, границу погрешности результата измерения находят путем построения композиции распределений случайных и неисключенных систематических погрешностей, рассматриваемых как случайные величины в соответствии с п. 4.3. Если доверительные границы случайных погрешностей найдены в соответствии с разд. 3 настоящего стандарта, допускается границы погрешности результата измерения 
(без учета знака) вычислить по формуле:
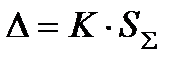
где K – коэффициент, зависящий от соотношения случайной и неисключенной систематической погрешностей;
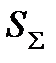- оценка суммарного среднего квадратического отклонения результата измерения.
Оценку суммарного среднего квадратического отклонения результата измерения вычисляют по формуле:
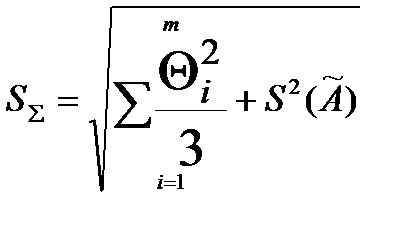
Коэффициент K вычисляется по формуле:
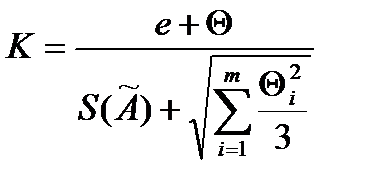
- Форма записи результатов измерений
a. Оформление результатов измерений – по ГОСТ 8.011-72.
При симметричной доверительной погрешности результатов измерений представляют в форме:
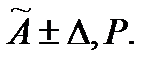
где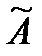 
- результат измерения.
Числовое значение результата измерения должно оканчиваться цифрой того же разряда, что и значение погрешности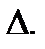 
b. При отсутствии данных о виде функций распределений составляющих погрешности результата и необходимости дальнейшей обработки результатов или анализа погрешностей, результат измерений представляют в форме:
; 
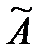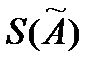, n; 
.
В случае, если границы неисключенной систематической погрешности вычислены в соответствии с п. 4.4, следует дополнительно указывать доверительную вероятность P.
Примечания
· Оценки 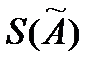и могут быть выражены в абсолютной и относительной формах.
· Определения терминов, встречающихся в стандарте, даны в справочном приложении 3.
