P-n- переходы получают в результате образования контакта между полупроводниками, изготовленными на основе одних и тех же химических элементов с разным типом электропроводности. На рис. 5 представлена типичная энергетическая диаграмма p-n– перехода в равновесном состоянии (без внешнего электрического поля). На этом же рисунке показано распределение носителей заряда. Поскольку электронные сродства и ширина запрещенной зоны контактирующих материалов одинаковые, разрыв зон D EC и D EV в плоскости металлургического контакта равен нулю; потенциальных барьеров здесь два и они одинаковые по величине.

Рис. 5. Энергетическая диаграмма и концентрация носителей заряда в равновесном p-n– переходе
Как видно, для основных носителей заряда (дырок для p- области и электронов для n- области) существует потенциальный барьер высотой q j0, для неосновных же носителей потенциального барьера не существует, и они проходят через p-n– переход беспрепятственно. В отличие от перехода Шоттки, контактная разность потенциалов довольно легко рассчитывается:
 .
.
Решая уравнение Пуассона можно получить распределение напряженности электрического поля и потенциала в p-n– переходе (рис. 6):

 (3)
(3)
Из уравнения (3) можно рассчитать общую толщину обедненной области
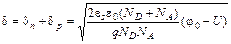 .
.

Рис.6. Распределение примеси, заряда, напряженности электрического поля
и потенциала в p-n– переходе
Для описания емкости пространственный заряд берется в одной из областей полупроводника (n или p) и равен
 .
.
Тогда емкость будет определяться
 .
.
Обычно диоды на основе p-n– переходов изготавливают с несимметричным легированием. Если, например,  , выражение для емкости упрощается:
, выражение для емкости упрощается:
 ,
,
т.е. величина емкости определяется только примесью слаболегированной области.
Следовательно, как и в случае барьера Шоттки, можно будет воспользоваться уравнением (2) для определения концентрации примеси, но только в одной из областей p-n– перехода.
Рассмотренная нами емкость получила название барьерной емкости. Её величина определяется неподвижными зарядами ионов легирующих примесей, без учета подвижных носителей заряда (электронов и дырок). Однако в p-n– переходе, в отличие от барьера Шоттки, происходит инжекция (впрыскивание) неосновных носителей заряда в соседние области. Это приводит к перераспределению основных носителей заряда, что происходит за счет процессов диффузии (рис. 7). Емкость, обусловленная этими зарядами, называют диффузионной.
Несмотря на то, что в установившемся состоянии примыкающие к p-n– переходу области не заряжены, диффузионную емкость можно связывать с зарядом инжектированных носителей, так как инжектированные носители и нейтрализующие их основные носители не исчезают. Для сравнения вспомним, что и обычный конденсатор в целом электрически нейтрален. Но в обычном конденсаторе положительный и отрицательный заряды пространственно разделены (то же самое можно сказать и о барьерной емкости p-n– перехода), в то время как при инжекции и положительный и отрицательный заряды оказываются в одной и той же области и пространственно не разделяются, в результате чего невозможно обнаружить область, где проходят токи смещения. В этом существенное отличие диффузионной емкости от барьерной емкости p-n- перехода и от емкости обычного конденсатора.

Рис. 7. Распределение носителей при изменении напряжения:
а,в – установившиеся состояния; б – нейтрализация заряда инжектированных носителей
Наличие диффузионной емкости приводит к тому, что эквивалентная схема диода на основе p-n– перехода становится более сложной по сравнению с диодом Шоттки (рис. 8).

Рис. 8. Эквивалентная схема диода с p-n– переходом
Барьерная и диффузионная емкости соединены параллельно, поэтому для раздельного их определения необходимо проводить измерения не на одной частоте. Однако следует отметить, что при обратных напряжениях изменение количества неосновных носителей (а, следовательно, и заряда, определяющего диффузионную емкость) будет незначительным, и тогда можно считать, что C диф << С бар. При прямых напряжениях этого утверждать нельзя, и емкости будут соизмеримы.






