а) Заметим, что 
член последовательности с номером 
равен 
и больше 
. Это и означает по определению, что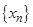 
– неограниченная последовательность.
б) Очевидно, что в интервале 
находятся все члены последовательности 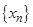с нечетными номерами, а значит, в этом интервале находится бесконечно много членов последовательности. Отсюда следует, что 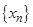не является бесконечно большой.
Теорема 1. Алгебраическая сумма конечного числа бесконечно малых последовательностей является бесконечно малой последовательностью.
Доказательство. Пусть 
и 
- бесконечно малые последовательности. Тогда для любого ε >0 существуют номера n 1(ε /2) и n 2(ε /2) такие, что для всех n > n 1(ε /2)выполняется неравенство | xn |< ε /2 и 
n 2(ε /2)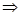 
| yn |< ε /2. Тогда, полагая n 0=max(n 1(ε /2), n 2(ε /2)), получим, что для любого n > n 1 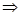| xn ± yn |≤| xn |+| yn |< ε /2+ ε /2= ε. Следовательно, { xn ± yn } – бесконечно малая последовательность.
Теорема 2. Произведение бесконечно малой последовательности на ограниченную является бесконечно малой последовательностью.
Доказательство. Пусть { хn } – бесконечно малая последовательность, а { уn } – ограниченная последовательность, т.е. существует такое число М >0, что для всех натуральных номеров выполняется неравенство │ yn │≤ М.
Зададим ε >0, в силу определения бесконечно малой последовательности существует такой номер N, что для всех n ≥ N выполняются неравенства │ xn │< 
. Поэтому для всех n ≥ N имеем │ xnyn │=│ xn ││ yn │< 
M = ε, что и означает, что последовательность { xnyn } бесконечно малая.
Следствие. Произведение конечного числа бесконечно малых последовательностей является бесконечно малой последовательностью.
Теорема 3. Если последовательность 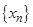– бесконечно большая, то начиная с некоторого номера определена последовательность 
, которая является бесконечно малой. Если последовательность 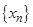– бесконечно малая и 
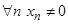, то последовательность является бесконечно большой.
Пример 2. Доказать, что последовательность 
является: а) бесконечно большой при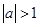 
; б) бесконечно малой при 
.
