Определение 1. Последовательность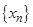 
называется бесконечно малой, если ее предел равен нулю, т.е. 
.
Определение 2. Последовательность 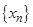называется бесконечно большой, если для всякого сколь угодно большого числа 
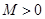существует такой номер 
, начиная с которого все члены последовательности удовлетворяют неравенству 
.
С геометрической точки зрения это означает, что в любой окрестности нуля находится лишь конечное число членов последовательности, а вне ее – бесконечно много.
Если последовательность 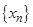– бесконечно большая, то пишут 
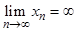. Если при этом, начиная с некоторого номера, все члены бесконечно большой последовательности положительны (отрицательны), то пишут 
(
). Отметим, что бесконечно большая последовательность не является сходящейся и символическая запись 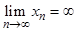означает только, что последовательность 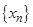является бесконечно большой, но вовсе не означает, что она имеет предел.
Всякая бесконечно большая последовательность является неограниченной, поскольку вне любой окрестности нуля имеется член последовательности (даже все члены, начиная с некоторого номера). Обратное неверно: неограниченная последовательность может и не быть бесконечно большой.
Пример 1. Пусть 
. Доказать, что последовательность 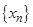: а) неограниченная; б) не является бесконечно большой.
