Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.
Из теоремы 3 следует, что сходящаяся последовательность имеет только одну предельную точку, совпадающую с ее пределом.
Из теоремы 4 следует, что всякая ограниченная последовательность имеет, по крайней мере, одну предельную точку.
Определение 5. Наибольшая (наименьшая) предельная точка последовательности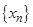 
, ограниченной сверху (снизу), называется верхним (нижним) пределом этой последовательности и обозначается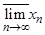 
.
Очевидно, если 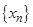сходится, то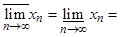 
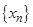. Если последовательность не ограничена сверху (снизу), то полагают 
.
Пример 2. Доказать расходимость последовательности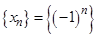 
.
Решение. Рассмотрим две подпоследовательности этой последовательности 
и 
(
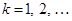). Очевидно, что 
, 
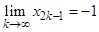. Таким образом, последовательность 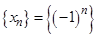имеет две предельные точки: 
и 
, а поэтому не может быть сходящейся, поскольку сходящаяся последовательность имеет только одну предельную точку.
Пример 3. Найти все предельные точки последовательности 
, верхний и нижний пределы этой последовательности.
Решение. Каждое из чисел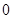 
, 
, 
, 
, 
, 
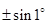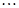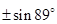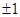встречается в последовательности бесконечно много раз, поскольку 
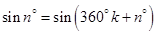. Поэтому каждое указанное число является предельной точкой последовательности . Других предельных точек последовательность не имеет, так как если число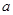 
не совпадает ни с одним из этих 181 чисел, то существует окрестность точки 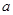, не содержащая ни одного члена последовательности. Из найденных 181 предельных точек наименьшей является , а наибольшей 1, т.е.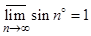 
, 
.
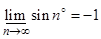