Кинетические закономерности технологических процессов

Экономическая эффективность пищевых производств в значительной степени зависит от скорости протекания технологических процессов.

Наука, изучающая механизм и скорость изменения характеристик процесса, называется кинетикой. В ее основе лежат закономерности, обусловливающие скорость процессов. Знание этих кинетических закономерностей необходимо для расчета параметров отдельных технологических процессов и аппаратов, в которых они происходят.

Установлен общий кинетический закон: скорость процесса прямо пропорциональна потенциалу и обратно пропорциональна сопротивлению системы.

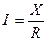или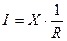

где I – скорость процесса

X – потенциал системы или движущая сила

R – сопротивление системы

 

Величину 1/R можно заменить обратной величиной - проводимости – L, тогда уравнение будет иметь вид:

I=L× X

Имея сведения о потенциале системы, или ее движущей силы, на основе этого общего кинетического уравнения можно получить расчетные уравнения для любого технологического процесса. Вспомним, что потенциал системы – это мера отклонения системы от равновесного состояния, а движущая сила – разница потенциалов в разных состояниях системы. Их определяют по градиентам температуры, давлений, концентраций. Проводимость (L) системы называют коэффициентом скорости процесса, или кинетическим коэффициентом. Под кинетическим коэффициентом понимают скорость процесса, потенциал которого равен единице. Это коэффициенты теплоотдачи, теплопроводности, константы скорости реакции и т.д.

 

Зная движущую силу конкретного процесса, воспользовавшись общим кинетическим уравнением, можем получить основное уравнение для любого процесса.

Для процесса теплопередачи

q = k D_t

где q – скорость переноса теплоты, удельный тепловой поток, Дж/(м²Кс);

k – коэффициент теплопередачи, Дж/(м² К с) или Вт/(м² К);

D_t – движушая сила, т.е. средняя разность температур, К или ⁰С.

 

Тепловой поток – это количество теплоты, переносимое через единицу поверхности в единицу времени,

q = Q/Ft

 

где Q – количество теплоты, Дж;

F - площадь поверхности, через которую передается теплота, м²;

t - время, с.

 

Для процесса массопередачи удельный поток массы [кг/(м² с)]

m =К _m DC

где К _m – коэффициент массопередачи, размерность которого зависит от размерности

концентрации, например, кг/[м² (кг/м³)с] либо м/с;

DC – движущая сила – средняя разность концентраций, кг/м³

 

m = М/Ft

где М – количество переносимого вещества, кг;

F - площадь поверхности, через которую осуществляется перенос, м²;

t - время, с.

 

Для гидродинамических процессов, например для фильтрования, кинетическое уравнение примет следующий вид:

V/ Ft = v = КDр

Где V – объем получаемого фильтрата, м³;

F - площадь поверхности, через которую осуществляется фильтрование, м²;

t - время, с;

v – скорость фильтрования, м³/(м² с) или м/с;

К – коэффициент, характеризщующий проводимость фильтрующей перегородки,

м³/(м²сПа) или м²с/кг;

Dр – разность давлений, Па.

 

Последнее уравнение известно в литературе как уравнение фильтрования Дарси.

Приведенные выше кинетические уравнения различных процессов получены нами из основного кинетического уравнения. Что демонстрирует единство материального мира. Еще более убедительно это единство проявляется при анализе дифференциальных уравнений, описывающих рассмотренные нами процессы.

Анализ общего кинетического уравнения показывает, что увеличить скорость процесса можно, увеличивая движущую силу либо уменьшая сопротивление. В этом состоит принцип интенсификации технологических процессов.

 

Если исследуемый конкретный процесс достаточно изучен и его можно описать дифференциальным уравнением или системой таких уравнений, то характеристики процесса находят аналитическими методами – методами математического моделирования процесса. К сожалению, для большинства технологических процессов пищевых производств эти методы не могут использоваться из-за того, что процессы очень сложной природы и не могут быть точно описаны дифференциальными уравнениями. Поэтому для расчета параметров этих процессов используют критериальные уравнения, в которых большое количество изменяемых величин дифференциального уравнения заменяют ограниченным числом безразмерных комплексов (критериев). Такие уравнения значительно простые и поэтому широко применяются.

Критериальное уравнение для конкретного сложного процесса составляют двумя путями: или на основе теории подобия с системой дифференциальных уравнений, которые не имеют аналитического решения, или на основе 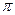- теоремы методом анализа размерностей. Первый путь используют для расчета известных процессов, а второй – в случае новых или мало изученных процессов.

После составления критериального уравнения с их помощью определяют подобные условия однозначности процесса и создают физическую модель – упрощенное подобие реального процесса. На модели производят серию опытов, целью которых является нахождение числовых значений кинетических коэффициентов. Такой способ их расчета получил название физического моделирования, поскольку при этом способе используются физические модели. Полученные с помощью критериальных уравнений параметры в дальнейшем используют для проектирования реального процесса или аппарата. Эти расчеты являются задачей дисциплины «Процессы и аппараты».