Уравнение регрессии математически описывает теоретическую линию регрессии. Теоретической линией регрессии называется та линия, вокруг которой группируются точки корреляционного поля, указывающие основное направление связи.
Для построения уравнения регрессии необходимо вычислить параметры теоретической линии связи.
Наиболее часто встречающиеся типы функции:
Линейная 
Параболическая 
Гиперболическая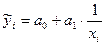 
Показательная 
Рассмотрим линейную функцию 
Основным методом решения задачи нахождения параметров уравнения связи является метод наименьших квадратов, разработанный Гауссом. Он состоит в минимизации суммы квадратов отклонений фактических значений от значений, вычисленных по уравнению связи
Для нахождения параметров 
и 
решают систему нормальных уравнений:
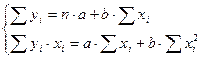
– показывает усредненное влияние всех прочих факторов, не включенных в исследование
(связь прямая), 
(связь обратная).
– коэффициент регрессии, показывает, на сколько в среднем изменится величина результативного признака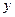 
при изменении факторного признака 
на натуральную единицу.
Коэффициент регрессии применяется для определения коэффициента эластичности, который показывает, на сколько процентов изменится величина результативного признака 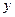при изменении факторного признака на 1%.
