Так как признаки варьируют, то состав единиц, попавших в выборку, может не совпадать с составом единиц по всей совокупности. Это значит, что обобщающие показатели в выборке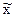 
и w могут отличаться от значений этих характеристик в генеральной совокупности р и 
.
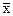Возможные расхождения между характеристиками выборочной и генеральной совокупности измеряются средней ошибкой выборки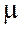 
.
В математической статистике доказывается, что значения средней ошибки выборки определяется по формуле:
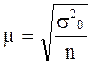
Предполагается, что известна генеральная дисперсия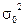 
. Но при выборочных обследованиях эти показатели не могут быть известны.
На практике для определения средней ошибки выборки обычно используются дисперсии выборочной совокупности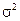 
. Эта замена основана на том, что при соблюдении принципа случайного отбора дисперсия выборки стремиться отобразить дисперсию в генеральной совокупности.
В математической статистике доказывается следующее отношение:
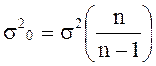
Если n достаточно велико, то 
1.
Например, если n =100, то =1,01 и т.д.
При замене генеральной дисперсии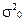 
дисперсией выборочной 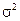формула расчета средней ошибки примет вид: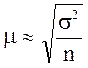 
При этом для показателя доли альтернативного признака дисперсия в выборочной совокупности определяется по формуле:
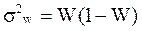
Для показателя средней величины дисперсия количественного признака в выборке определяется по формуле:
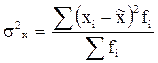
Формула для расчета ошибки применяется лишь при повторном методе отбора.
Сущность повторного отбора состоит в том, что каждая попавшая в выборку единица совокупности после фиксации значения должна быть возвращена в генеральную совокупность, где ей опять представляется равная возможность попасть в выборку.
На практике повторный отбор осуществляется редко. Обычно выборочное обследование проводится по схеме бесповторного отбора, при котором повторное попадание в выборку одних и тех же единиц исключено.
Посколько при бесповторном отборе численность генеральной совокупности в ходе выборки сокращается, то в формулу для расчета средней ошибки выборки включают дополнительный множитель 1-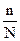 
. Формула средней ошибки выборки примет вид: 
.
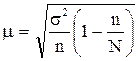Полученное значение средней ошибки необходимо для установления возможного значения .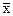
Одно из возможных значений средней определяется по формуле:
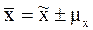
Итак, характеристика средней в генеральной совокупности отличается от средней 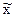на величину средней ошибки выборки 
.
Но такое суждение можно гарантировать не с абсолютной достоверностью, а лишь с определенной степенью вероятности.
В математической статистике доказывается, что пределы значений характеристик генеральной совокупности отличаются от характеристик выборочной совокупности лишь с вероятностью, которая определена числом 0,683.
Это означает, что в 683 случаях из 1000 генеральная средняя будет находиться в установленных пределах. В остальных 317 случаях они могут выйти за эти пределы. Вероятность можно повысить, если расширить пределы отклонений. Так, при удвоенном значении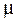 
, вероятность достигает 0,954.
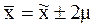
Если обозначить значение увеличения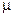 
за t, то можно записать в общем виде:
Множитель t называется коэффициентом доверия. Известный русский математик А.М.Ляпунов дал выражение конкретных значений множителя t для различных степеней вероятности в виде функции:
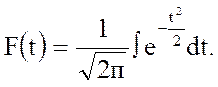
На практике пользуются готовыми таблицами этой функции.
| Крит. ошибка | Вероятность |
| 0,0 0,1 0,5 1,0 1,5 2,0 2,5 2,6 | 0,1 0,0797 0,3829 0,6827 0,8664 0,9545 0,9876 0,9907 0,9973 0,999937 |
Лишь с определенной степенью вероятности можно утверждать, что показатели генеральной совокупности и их отклонения не превысят величину t 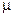. Величина t 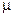называется предельной ошибкой выборки.
Тогда:
.
