Наряду с изучением признака по всей совокупности бывает необходимо проследить количественные изменения признака по группам, а так же между группами. Такое изучение вариации достигается посредством вычисления и анализа различных видов дисперсий.
Выделяют дисперсию общую, межгрупповую и внутригрупповую (случайная).
Общая дисперсия 
измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию:
Межгрупповая дисперсия 
(факторная) характеризует систематическую вариацию, т.е. различия в величине изучаемого признака, возникающее под влиянием признака-фактора, положенного в основание группировки. Она рассчитывается по формуле:
- средняя величина по отдельной группе
- численность признака по отдельной группе
Средняя из внутригрупповых дисперсий (случайная). Эта вариация возникает под влиянием не учитываемых факторов и не зависит от условия, положенного в основу группировки. Определяется по формуле:
Существует закон, связывающий 3 вида дисперсий, который называется правилом сложения дисперсий:
Пример:
Определить групповую дисперсию, среднюю из групповых, межгрупповую, общую дисперсию по данным таблицы:
Производительность труда 2-х бригад.
| № | Изгот. деталей |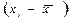 
| 
| № | Изгот. деталей |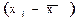 
|
|
| -2 -1 | -3 -2 -1 | ||||||
Для расчета вычислим среднюю по каждой группе
Подставляем промежуточные значения в формулу, получаем внутригрупповые дисперсии:
Средняя из внутригрупповых дисперсий:
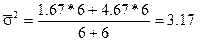
Рассчитаем общую среднюю:
Межгрупповая дисперсия:
Общая дисперсия по правилу сложения:
=3.17+9=12.17
Проверим, вычислим обшую дисперсию обычным способом
3. Анализ рядов распределения.
Основная задача анализа вариационных рядов – выявление подлинной закономерности распределения путем исключения влияния второстепенных, случайных для данного распределения факторов. Эта основная задача достигается путем увеличения объема исследуемой совокупности при одновременном уменьшении интервала ряда.
