Переменность окружной скорости по радиусу, варианты изменения треугольников скоростей по высоте лопатки.
Два фактора, вызывающие изменения параметров по радиусу:
1) 
- переменность окружной скорости по радиусу;
2) 
- увеличение градиента Р1 по радиусу.
Желание учесть эти факторы и привели к плоской модели.
Первая модель учитывала изменение окружной скорости по радиусу, эти методы «гидравлические» (повышают η на 3÷4%).
Методы, учитывающие u и 
, получили название аэродинамические (повышают к.п.д. еще на 3÷5%) см.рис.5.3.
Цель этого метода: обеспечить безударного течение потока по всей высоте лопатки.
Рис.5.3. Зависимость к.п.д. от разных методов закрутки
Аэродинамические методы закрутки.
5.3.1. Исходные положения,
Уравнения Навье-Стокса – это система дифференциальных уравнений, которая описывает движение вязкой ньютоновской жидкости либо газа. Так называемая «вязкость» жидкости – это её способность оказывать сопротивление, если какую-то её часть попытаться сдвинуть относительно соседнего слоя (например, при гребле). При этом в жидкости происходит внутреннее трение.
Ньютоновская жидкость – это жидкость, для которой скорость её деформации пропорциональна вязкости. Ньютоновская жидкость течет всегда, даже если силы, воздействующие на нее, очень малы – только бы они не были нулевыми. Типичная ньютоновская жидкость – вода. Вспомните, как она ведет себя в невесомости: это тот случай, когда на жидкость совсем не воздействуют внешние силы, даже сила тяжести.
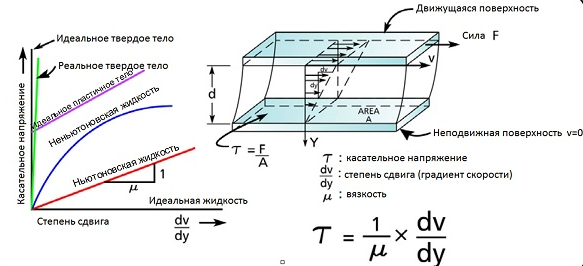
Рис. 5.4. Диаграммы жидкости и трёхмерная проекция
Существующие способы профилирования относительно высоких (длинных) лопаток основаны на использовании радиального равновесия потока в осевых зазорах. Рассмотрим ступень с цилиндрическими обводами (рис.5.5.).
Рис. 5.5. К выводу уравнения радиального равновесия
Выделим в осевом зазоре двумя цилиндрическими сечениями на радиусе r элементарное кольцо толщиной dr и шириной 
. Выделенное кольцо с массой 
вращается в осевом зазоре с окружной скоростью С1 u и на него действует центробежная сила dC.
где v 1 - удельный объем в зазоре на радиусе г.
Указанная центробежная сила уравновешивается силой dP1, обусловленной разностью давлений dP1 на наружной и внутренней поверхности выделенной частицы потока
.
Приравнивая силы dС и dP1 находим условие радиального равновесия потока в осевом зазоре
. (17.1)
При отсутствии потерь в сопловой решетке из уравнения количества движения имеем
.
Выражая из последнего уравнения dP1 и подставляя его в (17.1), получим
. (17.2)
Учитывая, что 
. (17.3)
Уравнение (17.2) и (17.3) являются исходными при выборе методов профилирования относительно высоких лопаток.
5.3.2. Свободно - вихревая закрутка
Алгоритм расчета, преимущества и недостатки.
Наиболее распространенным способом профилирования лопаток газовых турбин является закрутка лопаток по методу постоянной циркуляции. При этом обеспечивается безударный вход потока на рабочие лопатки и сохраняются постоянные по высоте лопаток осевые составляющие скоростей С1a за сопловой и С2а за рабочей решетками, что уменьшает неравномерность поля скоростей в ступени.
Дифференцируя уравнение 
, получим 
. После подстановки в выражение (17.2) имеем
. (17.4)
Проинтегрировав уравнение (17.4), получим условие постоянства поля осевых скоростей за сопловой решеткой при изоэнтропийном течении:
. (17.5)
Аналогично условие постоянства поля осевых скоростей за рабочей решеткой: C 2 u r = const.
Записывая полученные условия для корневого и произвольного сечений, а также учитывая соотношения треугольников скоростей получим зависимости для изменения углов α1, β1, β2 в сопловой и рабочей решетках по радиусу ступени при закрутке лопаток по методу постоянной циркуляции:
Полагая, что параметры рабочего тела перед ступенью и за ней не меняются, изменение степени реактивности в ступени по радиусу при условии постоянства коэффициента скорости φ определяется следующим образом
(17.6)
Особенностью ступени, спрофилированной по методу С1 a =const является постоянство работы во всех сечениях по высоте лопатки.
| № | Наименование величины | Обозначение | Размерность | Формула или источник | Численное значение | ||||
| rк | r1 | rср | r2 | rв | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | Расчетный радиус | r | м | ||||||
| 2 | Показатель степени | n | ¾ | j2 | |||||
| 3 | Окружная составляющая С1 | C1u | м/с | 
| |||||
| 4 | Осевая составляющая | C1z | м/с | const | |||||
| 5 | Абсолютная скорость выхода из соплового аппарата | C1 | м/с | 
| |||||
| 6 | Угол выхода потока из соплового аппарата | a1 | град. | 
| |||||
| 7 | Окружная скорость | U1 | м/с | 
| |||||
| 8 | Окружная составляющая W1 | W1u | м/с | C1u-U | |||||
| 9 | Относительная скорость на входе в рабочую решетку | W1 | м/с | 
| |||||
| 10 | Угол входа в рабочую решетку | b1 | град. |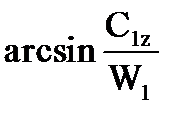 
| |||||
| 11 | Окружная составляющая С2 | C2u | м/с | 
| |||||
| 12 | Осевая составляющая С2 | C2z | м/с | const | |||||
| 13
| Абсолютная скорость и угол выхода потока из рабочей решетки | C2 | м/с | 
| |||||
| a2 | град. | a2cp | |||||||
| 14 | Окружная скорость | U2 | м/с | 
| |||||
| 15 | Окружная составляющая W2 | W2u | м/с | C2u+U2 | |||||
| 16 | Относительная скорость выхода из рабочей решетки | W2 | м/с | 
| |||||
| 17 | Угол выхода потока из рабочей решетки | b2 | град. | 
| |||||
| 18 | Степень реактивности | r | ¾ | 
| |||||
| 19 | Давление за сопловым аппаратом | Р1 | МПа | 
| |||||
| 20 | Окружная работа | lu | кДж/кг |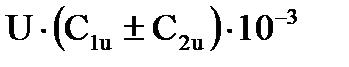 
| |||||
5.3.3. Закрутка по методу 
1=const,
Исходные уравнения, алгоритм расчета, преимущества и недостатки
Наиболее распространенным способом закрутки лопаток паровых турбин является закрутка их при сохранении неизменным угла выхода потока из сопловой решетки (α1=const). Достоинство рассматриваемого метода заключается в том, что сопловые лопатки ступени остаются цилиндрическими, что упрощает технологию их изготовления. Для определения закона изменения угла β2 по радиусу необходимо дополнительное условие. Чаще всего оно записывается в виде: Lu=const или β2=const по радиусу ступени.
| № | Наименование величины | Обозначение | Размерность | Формула или источник | Численное значение | ||||
| rк | r1 | rср | r2 | rв | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | Расчетный радиус | r | м | ||||||
| 2 | Угол выхода потока из соплового аппарата | a1 | град. | const | |||||
| 3 | Показатель степени | n1 | ¾ | j2×cos2a1 | |||||
| 4 | Окружная составляющая С1 | C1u | м/с | 
| |||||
| 5 | Осевая составляющая C1 | C1z | м/с | 
| |||||
| 6 | Абсолютная скорость выхода из соплового аппарата | C1 | м/с |
| |||||
| 7 | Окружная скорость | U | м/с |
| |||||
| 8 | Окружная составляющая W1 | W1u | м/с | C1u-U | |||||
| 9 | Осевая составляющая W1 | W1z | м/с | C1z | |||||
| 10 | Относительная скорость на входе в рабочую решетку | W1 | м/с |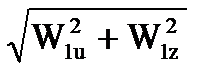 
| |||||
| 11 | Угол входа в рабочую решетку | b1 | град. | 
| |||||
| 12 | Угол выхода потока из рабочей решетки | a2 | град. | const | |||||
| 13 | Показатель степени | n2 | y2×cos2a2 | ||||||
| 14 | Окружная составляющая С2 | C2u | м/с | 
| |||||
| 15 | Осевая составляющая С2 | C2z | м/с | 
| |||||
| 16 | Абсолютная скорость выхода потока из рабочей решетки | C2 | м/с | 
| |||||
| 17 | Окружная скорость | U | м/с | 
| |||||
| 18 | Окружная составляющая W2 | W2u | м/с | C2u+U | |||||
| 19 | Осевая составляющая W2 | W2z | м/с | C2z | |||||
| 20 | Относительная скорость выхода из рабочей решетки | W2 | м/с | 
| |||||
| 21 | Угол выхода потока из рабочей решетки | b2 | град. | 
| |||||
| 22 | Степень реактивности | r | ¾ | 
| |||||
| 23 | Показатель адиабаты | k | ¾ | 1,035+0,1×x*0 | |||||
5.3.4. Особенности закрутки по методу 
cz= const.
