Геометрические характеристики турбинных профилей и решеток указаны на рисунке 2.15.
Шаг профилей в решетке оказывает существенное влияние на ее характеристики. С уменьшением шага возрастают профильные потери в связи с увеличением поверхности трения, омываемой единицей количества газа.
С увеличением шага давление на вогнутой поверхности профиля возрастает, на спинке – падаетРисунок 2.14. Это, с одной стороны вызывает увеличение концевых потерь, а с другой - способствует отрыву потока на спинке, где разность давления на выходе из решетки и минимального давления возрастает. Кроме того, снижение давления на спинке при увеличении шага может вызвать появление волновых потерь.
Очевидно, для каждого типа решетки должен существовать оптимальный шаг, при котором КПД решетки достигает максимума. Оптимальные значения шага лопаток должны определяться опытным путем для конкретных решеток и условий их обтекания. Для общей ориентировки можно принять: у реактивных решеток 
, у активных 
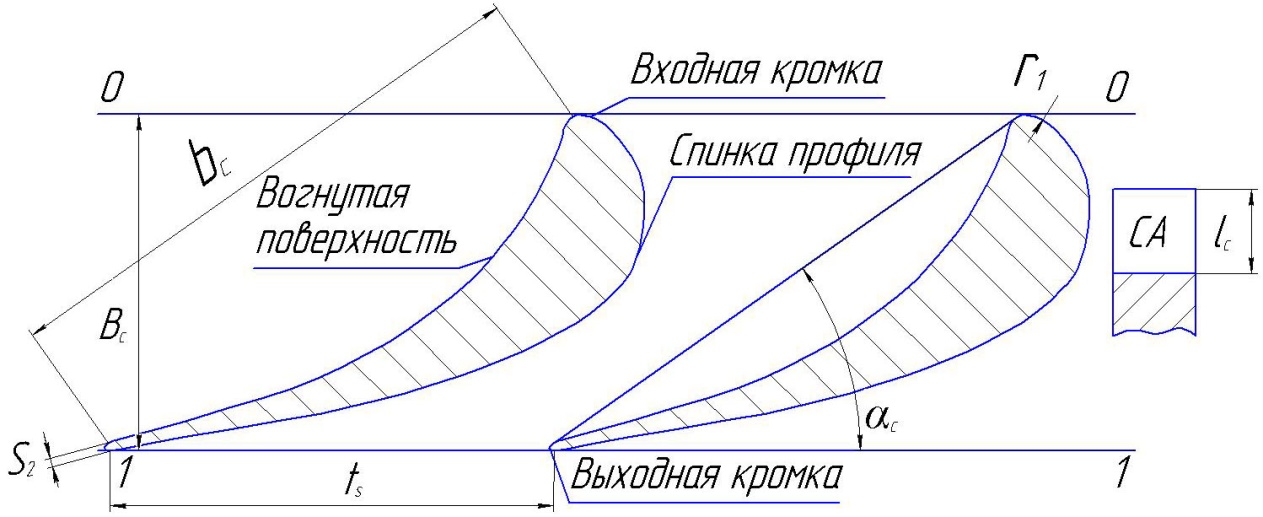
Рис.2.14. Профильный вид лопаток
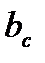- хорда профиля,
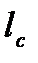- высота СЛ,
- радиус закругления входной кромки,
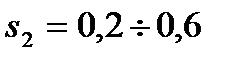, мм - толщина входной кромки,
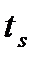- шаг установки профилей в СР,
- угол установки профиля в СР,
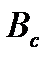- ширина СР.
Сечение 0-0 - передний фронт решетки,
Сечение 1-1 - задний фронт решетки.
Рис. 2.15.Геометрические характеристики турбинной ступени: а - продольный разрез и кольцевая решетка сопловых лопаток; б - плоские решетки профилей сопловых и рабочих лопаток; в - профиль рабочей лопатки.
Кинематические и аэродинамические характеристики течения потока в сопловой и рабочей решетках.
При выборе ширины рабочих лопаток необходимо помнить о том, что уменьшение ширины повлечет за собой увеличение числа лопаток и может вызвать трудность в размещении их на диске. Кроме того, в узких лопатках по прочностным и технологическим соображениям не всегда удается выдержать оптимальные толщины входной и выходной кромок. Лопатки газовых турбин чаще всего выполняются с шириной В=(0,25+0,4) 
.
При выборе взаимного расположения сопловых и рабочих лопаток необходимо обращать внимание на величину осевого зазора между решетками и соотношения между высотами сопловых и рабочих лопаток.
Чем больше осевой зазор между сопловой и рабочей решетками, тем сильнее выравнивается поток, поступающий на рабочие лопатки, тем меньше потери энергии от нестационарности. Однако с увеличением осевого зазора повышаются потери от трения на торцевых ограничивающих поверхностях. В каждом частном случае должен существовать оптимальный осевой зазор, величина которого тем больше, чем неравномернее поле скоростей на выходе из сопловой решетки. Однако, кроме указанных факторов, надо учитывать еще утечку или подсос газа через осевой зазор, которые вызывают дополнительные искривления линий тока в периферийных областях. На основании проведенных экспериментов рекомендуется принимать величину осевого зазора в пределах 
.
Коэффициенты потерь и к.п.д. решеток.
Поворот потока в решетке оказывает влияние на ее КПД. Поворот увеличивается с уменьшением суммы углов β1+β2 для рабочей решетки и суммы углов α2+α1 для сопловой решетки. (рис 2.16) При этом возрастает протяженность диффузорного участка на спинке и повышается опасность отрыва потока, также повышаются концевые потери вследствие интенсификации вторичных течений. С увеличением угла поворота потока коэффициенты скорости 
или 
уменьшаются.
Снижение относительной высоты лопаток 
вызывает уменьшение КПД решетки и, следовательно, коэффициентов 
, 
. При 
относительная величина концевых потерь незначительна, однако она резко возрастает при малых значениях 
.
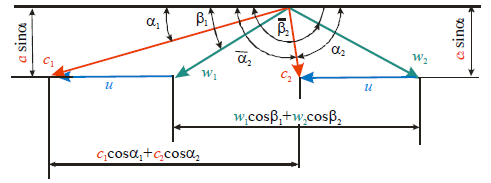
Рис. 2.16. Совмещенные треугольники скоростей турбинной ступени.
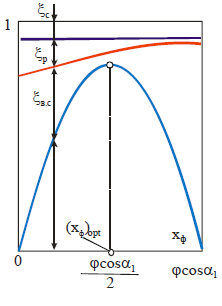
Найденное параболическое протекание кривой КПД определяется изменением отдельных потерь в зависимости от x ф. Очевидно, что зависимость η ол может быть непосредственно путем подсчета потерь в решетках и потери с выходной скоростью при x ф разных и при соблюдении принятых ранее допущений. Выражая потери в долях располагаемой энергии и вычитая сумму потерь из единицы, мы должны получить ту же кривую для КПД ступени
Проведенный таким образом расчет позволяет построить кривые изменения отдельных потерь в зависимости от x ф (рис. 2.17).
