В общем случае задача выбора оптимальных сроков службы элементов может быть решена одним из методов численного программирования, например методом случайного поиска, который не гарантирует отыскания точного решения, но в тех случаях, когда мы не располагаем достаточным машинным временем для организации полного перебора, он оказывается полезным.
Рассмотрим частную задачу определения рационального срока службы элемента КСНО, исходя из минимума средних ежегодных затрат за все время эксплуатации. С такой задачей часто приходится встречаться при проектировании нового комплекса, чтобы основные узлы и агрегаты рассчитывать именно на этот срок.
Различают три срока службы технического устройства КСНО:
— физический  , по достижении которого устройство к эксплуатации непригодно и ремонту не подлежит;
, по достижении которого устройство к эксплуатации непригодно и ремонту не подлежит;
— экономический  , обеспечивающий минимальные затраты на эксплуатацию, включая и затраты на приобретение;
, обеспечивающий минимальные затраты на эксплуатацию, включая и затраты на приобретение;
- рациональный  , учитывающий помимо экономичности реальные возможности государства по обновлению элементов КСНО и занимающий промежуточное положение между
, учитывающий помимо экономичности реальные возможности государства по обновлению элементов КСНО и занимающий промежуточное положение между  и
и  .
.
При проектировании следует стремиться к тому, чтобы физический срок службы совпадал с рациональным, поскольку увеличение физического срока службы влечет за собой увеличение стоимости элемента КСНО.
Годовая стоимость эксплуатации  элемента КСНО может быть представлена в виде следующей зависимости:
элемента КСНО может быть представлена в виде следующей зависимости:
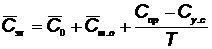 , (5.55)
, (5.55)
где  — годовые расходы, не зависящие от срока службы (заработная плата обслуживающего персонала и т. п.);
— годовые расходы, не зависящие от срока службы (заработная плата обслуживающего персонала и т. п.);  — годовые расходы на техническое обслуживание и ремонт;
— годовые расходы на техническое обслуживание и ремонт;  — стоимость приобретения элемента КСНО;
— стоимость приобретения элемента КСНО;  — стоимость, возвращаемая при сдаче элемента КСНО в утиль; Т — срок службы.
— стоимость, возвращаемая при сдаче элемента КСНО в утиль; Т — срок службы.
Годовые расходы на техническое обслуживание и ремонт являются функцией времени эксплуатации. Вид этой функции аналогичен функции интенсивности отказов (см. рис. 5.7). Для практических целей можно пользоваться линейной аппроксимацией этой зависимости, поскольку экономический срок службы выбирается на линейном участке, т. е.  .
.
Средние годовые затраты на техническое обслуживание и ремонт за весь срок службы будут, очевидно,
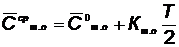 , (5.56)
, (5.56)
а средняя годовая стоимость эксплуатации элемента КСНО с учетом зависимостей (5.55)и (5.56) определится по формуле
 . (5.57)
. (5.57)
С течением времени производство элемента КСНО становится дешевле, а поэтому уменьшается и стоимость приобретения. Это уменьшение обычно подчиняется закону
 , (5.58)
, (5.58)
где  — стоимость приобретения к начальному периоду времени;
— стоимость приобретения к начальному периоду времени;  — статистический коэффициент.
— статистический коэффициент.
Уменьшение стоимости приобретения, которое за время Т составит  , приводит к увеличению средних годовых затрат на эксплуатацию:
, приводит к увеличению средних годовых затрат на эксплуатацию:
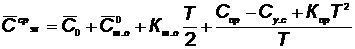 . (5.59)
. (5.59)
Для определения экономического срока службы элемента КСНО необходимо взять производную от  по T и приравнять ее нулю. После преобразований будем иметь
по T и приравнять ее нулю. После преобразований будем иметь
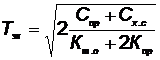 . (5.60)
. (5.60)
Определив экономический срок службы и исходя из потребностей данного элемента КСНО, выбирают рациональный срок службы.
Необходимое количество произведенных элементов КСНО за время t с учетом необходимости замены вышедших по срокам эксплуатации определяется по формуле

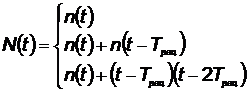 при
при
при
при
(5.61)
где  — ежегодная потребность в элементах КСНО.
— ежегодная потребность в элементах КСНО.






