Наиболее важной характеристикой, объединяющей свойства ЛА, КСНО и условия их применения, является эффективность комплекса ЛА данного типа. Она характеризует степень пригодности комплекса по назначению.
Эффективность КСНО является составной частью эффективности комплекса ЛА и может быть представлена в виде произведения двух независимых случайных величин:
 (4.45)
(4.45)
где РГ.П — вероятность готовности КСНО к применению; Рн.ф.р — вероятность нормального функционирования элементов КСНО при выполнении задачи.
Вероятность готовности КСНО к применению характеризует два независимых случайных события:
— вероятность того, что в произвольный момент времени комплекс будет находиться в исправном состоянии;
— вероятность того, что в нужный момент времени комплекс не будет поражен противником, т. е.
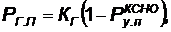 (4.46)
(4.46)
где КГ — коэффициент готовности КСНО, определяющий вероятность того, что в произвольный момент времени комплекс будет находиться в исправном состоянии;
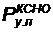 — условная вероятность поражения КСНО.
— условная вероятность поражения КСНО.
Определение коэффициента готовности КСНО. Процесс эксплуатации КСНО можно представить как чередование периодов исправного и неисправного состояний (рис. 4.5, где А — нерабочее состояние, комплекс исправен; В — рабочее состояние, комплекс исправен; С — нерабочее состояние, неисправность не выяснена; D — состояние восстановления).
Переходы из одного состоянии в другое характеризуются следующими интенсивностями:
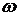 — средняя (отнесенная к сроку эксплуатации) интенсивность назначений на работу;
— средняя (отнесенная к сроку эксплуатации) интенсивность назначений на работу;
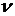 — средняя интенсивность выполнения работы (величина, обратная средней продолжительности одного периода работы)
— средняя интенсивность выполнения работы (величина, обратная средней продолжительности одного периода работы)
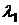 — средняя интенсивность возникновения отказов в нерабочем состоянии;
— средняя интенсивность возникновения отказов в нерабочем состоянии;
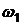 — средняя интенсивность работ по обнаружению неисправностей (внешние осмотры и другие виды контроля, не связанные с наработкой комплекса);
— средняя интенсивность работ по обнаружению неисправностей (внешние осмотры и другие виды контроля, не связанные с наработкой комплекса);
 — средняя интенсивность возникновения отказов в рабочем состоянии;
— средняя интенсивность возникновения отказов в рабочем состоянии;
 — средняя интенсивность восстановления.
— средняя интенсивность восстановления.
Функционирование комплекса происходит следующим образом. Из состояния А комплекс может перейти либо в состояние В, либо в С. Назначение комплекса на работу соответствует переходу в В и идет с интенсивностью 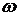 . После работы исправный комплекс переходит в состояние А. Если во время работы происходит отказ, то комплекс с интенсивностью
. После работы исправный комплекс переходит в состояние А. Если во время работы происходит отказ, то комплекс с интенсивностью  переходит в состояние D. Беля отказ возник в состоянии А, то комплекс переходит в состояние С с интенсивностью
переходит в состояние D. Беля отказ возник в состоянии А, то комплекс переходит в состояние С с интенсивностью 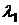 , а восстановление идет с интенсивностью
, а восстановление идет с интенсивностью  . После восстановления — переход в А, назначение же на работу из состояния С происходит с интенсивностью
. После восстановления — переход в А, назначение же на работу из состояния С происходит с интенсивностью 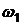 .
.
Необходимо отметить, что в состоянии С могут возникать неисправности с той же интенсивностью, что и в состоянии А. Однако возникновение этих новых неисправностей не означает перехода в другое состояние: комплекс продолжает оставаться в состоянии С до тех пор, пока не будет установлено, что он неисправен.
Возникновение в нерабочий период двух и более неисправностей отражается на затратах времени на восстановление. Как правило, межрегламентный период эксплуатации меньше среднего времени нахождения в исправном состоянии, когда комплекс не работает. Поэтому вероятность возникновения более одной неисправности в период между работами можно считать малой.
В произвольный момент времени комплекс может находиться только в одном состоянии. Определим вероятности пребывания комплекса в каждом состоянии.
Будем считать, что потоки переходов с интенсивностями  являются стационарными пуассоновскими, а процесс функционирования комплекса в этом случае можно считать марковским.
являются стационарными пуассоновскими, а процесс функционирования комплекса в этом случае можно считать марковским.
Стационарным потоком событий называется поток, для которого вероятность появления того или другого числа событий на участке времени  зависит лишь от длины этого участка и не зависит от того, где по оси времени взят этот участок.
зависит лишь от длины этого участка и не зависит от того, где по оси времени взят этот участок.
Пуассоновский поток — это поток, обладающий свойствами ординарности и отсутствия последействия.
Поток событий называется ординарным, если вероятность того, что на малый участок Δt, примыкающий к моменту времени t, падает больше одного события, пренебрежимо мала по сравнению с вероятностью того, что на этот же интервал времени попадает ровно одно событие.
Отсутствие последействия заключается в том, что для любых пересекающихся участков  и
и 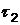 число событий, попадающих на один из них, не зависит от того, сколько событий попало на другой.
число событий, попадающих на один из них, не зависит от того, сколько событий попало на другой.
Процесс называется марковским, если состояние системы Xi в некоторый момент времени определяет лишь вероятность Pij (t) того, что через промежуток времени t система будет находиться в состоянии Xj, причем эта вероятность не зависит от течения процесса в предшествующий период.
Вероятность нахождения комплекса в каком-либо из состояний (А, В, С, D) обозначим PA (t), PB (t), Pc (t), PD (t). Составим уравнения, описывающие этот процесс.
Если вероятность нахождения комплекса в состоянии А была PA (t), то в момент времени (t + Δ t) вероятность нахождения комплекса в состоянии A PA (t + Δ t) будет определяться следующим образом:
а) вероятность того, что в момент t комплекс находился в состоянии А и за время Δ t не перешел ни в какое другое состояние, будет
 ; (4.47)
; (4.47)
б) вероятность того, что в момент времени t комплекс находился в состоянии B и за время Δt перешел в состояние А, определяется выражением
 (4.48)
(4.48)
в) вероятность того, что в момент времени t комплекс находился в состоянии D и за время Δt перешел в состояние А, находится так:
 (4.49)
(4.49)
г) вероятность перехода комплекса из состояния С в состояние А равна нулю.
Поскольку вероятность того, что за малый промежуток времени произойдет больше одного события, пренебрежимо мала (поток событий ординарный), то вероятность нахождения комплекса в момент времени (t + Δt) в состоянии А определяется по теореме сложения вероятностей:
 (4.50)
(4.50)
Отбрасывая величины второго порядка малости и деля на Δt, а также учитывая, что  , получаем
, получаем
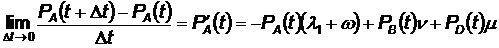 . (4.51)
. (4.51)
Аналогично получаются уравнения для других состояний:
 (4.52)
(4.52)
Для нахождения коэффициента готовности достаточно иметь стационарное решение, т. е. найти предельные вероятности состояний при достаточно большом t. Так как при  то стационарная система уравнений имеет вид
то стационарная система уравнений имеет вид
 (4.53)
(4.53)
Последнее уравнение необходимо добавить потому, что вероятности РА, Р B,, Р C, и, PD составляют полную систему событий. Решая эту систему, получаем
 (4.54)
(4.54)
где 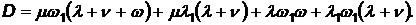
Вероятность исправного состояния комплекса систем наземного обеспечения в произвольный момент времени (коэффициент готовности) определяется формулой КГ = РА+Р B:
 . (4.55)
. (4.55)
Возможны некоторые частные случаи:
а) случай, когда по условию эксплуатации можно пренебречь интенсивностью или вероятностью возникновения неисправностей в нерабочий период, т.е. пребывания комплекса в состоянии С невозможно, тогда  и
и

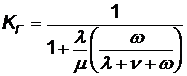 ; (4.56)
; (4.56)
б) случай нерабочего периода, когда для выявления неисправностей проводятся кратковременные проверки, не связанные с наработкой комплекса, т. е. состояние В отсутствует, тогда  и
и
 (4.57)
(4.57)
в) случай характерен для комплексов, находящихся длительное время в рабочем состоянии, и готовность в этом случае
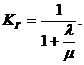 (4.58)
(4.58)
Оценка вероятности поражения КСНО. При проектировании КСНО необходимо учитывать возможность его поражения от взрыва. В зависимости от расположения элементов КСНО на ТП и СП, а также от мощности возможного взрыва или серии взрывов вероятность поражения КСНО целесообразно определять либо с учетом эффекта накопления ущерба, либо без учета этого эффекта.
Эффект накопления ущерба необходимо учитывать для крупномасштабных КСНО, когда возможный взрыв ЛА на пусковом устройстве, а также взрывы отдельных объектов СП или ТП не приводят к полному выводу из строя всего комплекса, а поражение происходит по мере накопления ущерба, т. е. вывода со строя все большего количества элементов КСНО. В зависимости от “живучести” отдельных элементов КСНО может быть вычислен условный закон поражения G (m) всего комплекса. Зная закон поражения, можно, используя формулу Колмогорова, определить вероятность поражения КСНО, имеющего N взрывоопасных объектов:
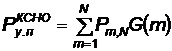 , (4.59)
, (4.59)
где Рт, N, — вероятность того, что из N возможных взрывов произойдет ровно m (из N взрывоопасных объектов взорвется ровно m). При условии, что взрывы отдельных объектов происходят независимо друг от друга, эта вероятность будет
 (4.60)
(4.60)
где  — число сочетаний из N по т; Р1, — вероятность появления одного взрыва на ТП или СП.
— число сочетаний из N по т; Р1, — вероятность появления одного взрыва на ТП или СП.
Если системы наземного обеспечения располагаются на относительно небольшой территории и любой единичный взрыв приводит к выводу из строя всего КСНО, вероятность поражения комплекса, имеющего N взрывоопасных элементов:
 . (4.61)
. (4.61)
Взрыв на ТП или СП может произойти либо в связи с аварийной ситуацией (взрыв ЛА на ПУ, пожар в хранилище компонентов топлива или в зоне, где проводятся работы с пиротехническими устройствами), либо в результате нанесения удара противником.
Уменьшение вероятности появления аварийной ситуации в процессе подготовки ЛА к пуску обеспечивается соблюдением правил техники безопасности при проведении работ с взрывоопасными компонентами, а также высокой квалификацией обслуживающего персонала, работающего в специальных помещениях на соответствующем оборудовании.
При нанесении удара противником вероятность появления взрыва на ТП или СП определяется как условная вероятность попадания на территорию расположения элементов КСНО боевого заряда. Если действительную поверхность расположения наземного комплекса аппропксимировать равновеликим прямоугольником со сторонами L X и LY, то эта вероятность выражается с помощью табличной функции Лапласа
 , (4.62)
, (4.62)
где Е X, Е Y — вероятные отклонения в направлении главных осей рассеивания О x и О y. Функция Лапласа есть выражение вида
 . (4.63)
. (4.63)
При определении условной вероятности поражения КСНО зарядами большой мощности часто КСНО может рассматриваться как ”точечный” объект, поскольку его линейный размер (например, диаметр равновеликого круга) не больше 0,2 радиуса поражения взрыва.
Вероятность поражения такого малоразмерного объекта определяется, как вероятность его накрытия зоной сплошного поражения, размеры которой определяются мощностью и местом взрыва, а также элементов КСНО и точкой возможного взрыва. Обычно ошибки пусков ЛА подчиняются нормальному закону распределения и рассеивание считается круговым. В этом случае условная вероятность поражения (для кругового ступенчатого закона поражения 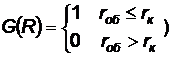 равна вероятности попадания в круг радиусом rk, равным радусу сплошного поражения от действия взрыва:
равна вероятности попадания в круг радиусом rk, равным радусу сплошного поражения от действия взрыва:
 (4.64)
(4.64)
где Е — круговое вероятное отклонение.
Радиус зоны сплошного поражения r к определяется как максимальное горизонтальное удаление цели от эпицентра взрыва, на котором объект может быть безусловно поражен действием ударной волны. Считаем, что
 , (4.65)
, (4.65)
где Кп — коэффициент “живучести” объекта, зависящий от минимального избыточного давления, приводящего к разрушению объекта; Q — тротиловый эквивалент возможного взрыва.
Анализ известных зависимостей показывает, что избыточное давление во фронте ударной волны Δр (единица измерения — бар), создаваемое при наземном взрыве на расстоянии r км от точки взрыва тротиловым эквивалентом в Q Мт, может быть определено, в частности, по следующей эмпирической формуле:
 . (4.66)
. (4.66)
Из этой формулы в результате решения квадратного уравнения относительно т будем иметь
 , (4.67)
, (4.67)
где  .
.
Подставляя в эту формулу минимальное избыточное давление Δр min, приводящее к разрушению объекта, получаем радиус зоны сплошного поражения
 , (4.68)
, (4.68)
где  — коэффициент “живучести” объекта.
— коэффициент “живучести” объекта.
Тогда условная вероятность поражения КСНО (4.64) будет определяться как
 . (4.69)
. (4.69)
При условии, что производится N независимых пусков, условная вероятность поражения КСНО будет
 . (4.70)
. (4.70)
Из четырех величин, входящих в зависимость (4.70), три (N, Q и E) представляют собой характеристики ЛА и головных частей и одна Δр min — характеристику степени защищенности КСНО от воздействия ударной волны.
Анализ зависимостей (4.69) и (4.70) показывает, что наземный взрыв, целью которого является поражение защищенного КСНО, например ШПУ, будет наиболее действенным при условии, что точность попадания очень высока, т. е. взрыв произойдет в непосредственной близости. Для современных ШПУ максимально допустимое избыточное давление составляет около 7,0 МПа, а для сверхзащищенных ШПУ эта величина доведена до 42,0 МПа.
Следовательно, зона существенного поражения ШПУ от наземного взрыва ограничена размерами образовавшейся воронки и навала грунта, выброшенного на поверхность из этой воронки.
Радиус воронки при наземном взрыве зависит в основном от мощности заряда и свойств грунта и определяется по формуле
 , (4.71)
, (4.71)
где  — радиус видимой воронки (при наземном взрыве), м; Q — мощность заряда, кт.
— радиус видимой воронки (при наземном взрыве), м; Q — мощность заряда, кт.
Глубина образовавшейся воронки будет составлять
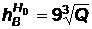 , (4.72)
, (4.72)
где  — глубина воронки, м; Q — мощность заряда, кт.
— глубина воронки, м; Q — мощность заряда, кт.
Радиус воронки при взрыве зависит как от мощности заряда, так и от глубины, на которой он произошел.
Получена эмпирическая зависимость между радиусом видимой воронки, глубиной взрыва и мощностью:
 , (4.73)
, (4.73)
где  — радиус видимой воронки, м; Н — глубина подрыва, м; Q — мощность, кт; знак «-» берется до оптимальной глубины взрыва, а на больших глубинах берется «+».
— радиус видимой воронки, м; Н — глубина подрыва, м; Q — мощность, кт; знак «-» берется до оптимальной глубины взрыва, а на больших глубинах берется «+».
Из этой формулы видно, что максимальный радиус видимой воронки будет определяться по формуле
 , (4.74)
, (4.74)
полученной из зависимости (4.73) при условии, что выражение в круглых скобках равно нулю:
 . (4.75)
. (4.75)
Выражение (4.75) позволяет определить оптимальную глубину взрыва, т. е. глубину, на которой необходимо взорвать заряд, чтобы получить максимальный радиус видимой воронки:
 , (4.76)
, (4.76)
где Н opt,— глубина, м; Q — мощность, кт.
Для определения минимальной глубины взрыва, когда радиус видимой воронки равен нулю, т. е. когда на поверхности нет воронки (камуфлетный взрыв), воспользуемся формулой (4.73) (со знаком «+»), положив  = 0.
= 0.
Имеем
 . (4.77)
. (4.77)
Таким образом, для поражения сильно защищенных ШПУ целесообразно подрыв заряда производить не на поверхности земли, а на оптимальной глубине, определяемой по формуле (4.76).
Сравним вероятности выживания ШПУ при условии, что круговые вероятностные отклонения равны, радиус зоны сплошного поражения ограничен радиусом видимой воронки для наземного взрыва и взрыва на оптимальной глубине.
Для наземного взрыва условная вероятность поражения ШПУ
 . (4.78)
. (4.78)
Для взрыва на оптимальной глубине эта величина определяется по формуле
 . (4.79)
. (4.79)
Вероятность “выживания” — это величина, противоположная условной вероятности поражения ШПУ (q =1- P). Для наземного взрыва она будет
 , (4.80)
, (4.80)
а для взрыва боевой части на оптимальной глубине
 . (4.81)
. (4.81)
Возьмем отношение этих величин:
 . (4.82)
. (4.82)
Это отношение показывает, во сколько раз вероятность “выживания” ШПУ при взрыве заряда на оптимальной глубине меньше, чем вероятность “выживания” такой же ШПУ при взрыве заряда на поверхности грунта. Например, для случая взрыва заряда в 1 кт, при значении кругового вероятного отклонения Е = 19,5 м, это отношение будет равно е, т. е. в 2,71 раза вероятность выживания при наземном взрыве больше, чем при взрыве на оптимальной глубине.






