Моделирование процесса функционирования ЦЗС

 

Выше указывалось, что процесс заправки ЛА через ЦЗС представляет собой последовательное изменение числа подготавливаемых к заправке, находящихся одновременно под заправкой ЛА и аппаратов, на которых проводятся послезаправочные операции. Указывалось также, что система обслуживания ЛА через ЦЗС может быть отнесена к системе массового обслуживания разомкнутого типа с неограниченным ожиданием.

Определение параметров, характеризующих процесс обслуживания ЛА в этом случае, осуществляется путем исследования n -канальной системы массового обслуживания, на вход которой поступает простейший поток заявок с интенсивностью λ _и и интенсивностью обслуживания каждого канала μ _и. Если поступившая заявка застает свободным хотя бы один канал, она немедленно принимается на обслуживание и обслуживается до конца, в противном случае заявка попадает в очередь с максимальным количеством мест в очереди m. Очевидно, при m = 0 получается система массового обслуживания с отказами, а при m  — система с ожиданием. Каждая заявка может обслуживаться либо одним каналом (нет взаимопомощи между каналами), либо несколькими свободными каналами (есть взаимопомощь между каналами).

Если отсутствует взаимопомощь между каналами обслуживания, состояние системы массового обслуживания разомкнутого типа описывается с помощью следующей системы дифференциальных уравнений:

  (4.9)

где P_k (t) - вероятность того, что в момент времени t система будет находиться в состоянии Х_к;

Х_к — в системе имеется k заявок и они обслуживаются k каналами, очереди нет;

  Х _{n + l} — в системе имеется n + l заявок, причем n из них обслуживается и l заявок находятся в очереди.

Интегрирование этой системы дифференциальных уравнений совместно с нормировочным условием

                                                                (4.10)

позволяет найти все вероятные состояния системы массового обслуживания в произвольный момент времени в процессе выхода системы на стационарный режим, т. е. в процессе постановки ЛА на работу.

При стационарном режиме работы рассматриваемой системы массового обслуживания система уравнений (4.9) превращается в систему алгебраических уравнений вида

                                      (4.11)

которая решается совместно с нормировочным условием (4.10) и дает следующие зависимости для определения вероятностей нахождения системы в состояниях Х_к и Х _{n + l}:

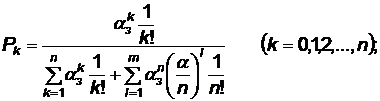                          (4.12)

 

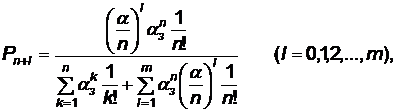                      (4.13)

где α₃ = λ/ μ — среднее число заявок, поступающих в рассматриваемую систему за среднее время обслуживания одной заявки одним каналом.

Зная вероятные состояния системы в любой момент времени, легко определить все параметры, характеризующие работу системы массового обслуживания.

Так, вероятность обслуживания заявки определяется вероятностью того, что к моменту поступления ее на обслуживание будут свободны хотя бы один канал или одно место в очереди:

            ,                               (4.14)

где Р _{n + m} определяется по формуле (4.15).

Далее может быть определено среднее число занятых каналов:

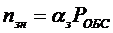       ^.                                                                                 (4.15)      

Вероятность занятости любого канала в произвольный момент времени определится по формуле:

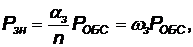                                                              (4.16)

где n — количество каналов обслуживания; ω₃ — среднее число заявок, поступающих в систему за среднее время обслуживания всеми каналами.

Вероятность того, что система полностью загружена, равна вероятности того, что в системе заняты все каналы:

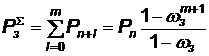                   .                               (4.17)

Среднее время неполной загрузки определяется из выражения

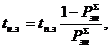                                                                                 (4.18)

где  - среднее время полной загрузки системы.

Среднее число заявок, находящихся в очереди:

                               .                                               (4.19)

Среднее время ожидания заявок в очереди

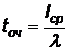                    .                                                    (4.20)

Среднее время нахождения заявки в системе складывается из среднего времени ожидания и обслуживания:

                            .                                       (4.21)

Таким образом определены основные параметры, характеризующие качество работы централизованной системы заправки при отсутствии взаимопомощи между каналами обслуживания.

Если существует взаимопомощь между каналами обслуживания, состояние системы массового обслуживания описывается с помощью системы дифференциальных уравнений вида

    (4.22)

которая в стационарном состоянии превращается в систему алгебраических уравнений

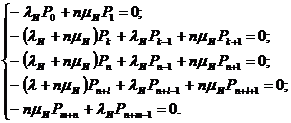                                           (4.23)

Параметры, характеризующие работу такой системы массового обслуживания, определяются выражениями, аналогичными (4.14)-(4.21), в которых вероятности нахождения системы в состояниях Х _k и X_{n + l} находятся путем интегрирования системы уравнений (4.23) совместно с нормировочным условием (4.10) для случая постановки ЛА на дежурство и решением системы уравнений (4.23) и (4.10) для стационарного режима работы ЦЗС с взаимопомощью между агрегатами обслуживания. В частности, для стационарного режима работы вероятность пребывания системы в j -м состоянии (j = 0, 1, 2,..., k,..., n,..., n + l,..., n + m) находится из выражения

                                                   (4.24)

                                                           (4.25)

где — среднее число заявок, поступающих в систему за среднее время обслуживания всеми каналами.