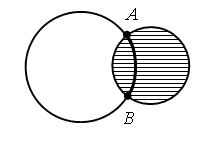
– Рассмотрите рисунок на доске:

– Объясните, что обозначают выражения, используя данный рисунок.

– Какое выражение более удобно в записи?
– Сегодня на уроке составим таблицу умножения на 3.
IV. Изучение нового материала.
Задание № 1 (с. 86).
– Рассмотрите иллюстрацию на с. 86. Сколько столовых приборов получил каждый гость? (По три прибора.)
– Сколько гостей должны прийти?
– Сколько же понадобилось столовых приборов?
– Как решил эту задачу Волк? (3 + 3 + 3 + 3 + 3 = 15.)
– Как решил задачу Заяц? (3 · 5 = 15.)
– Кто из них решил эту задачу быстрее? Почему?
Далее учащиеся составляют и записывают в тетрадь таблицу умножения трех.
Задание № 2 (с. 87).
Используя карточку-помощницу, фишки, учащиеся находят значение произведений.
Задание № 3 (с. 87).
Учащиеся сравнивают значения произведений, используя калькулятор.
3 · 8 равно 8 · 3, так как 3 · 8 = 24 и 8 · 3 = 24;
3 · 6 равно 6 · 3, так как 3 · 6 = 18 и 6 · 3 = 18.
Вывод: от перестановки множителей значение произведения не изменяется.
Задание № 4 (с. 87).
Используя цветные фишки, учащиеся находят значение произведений:
3 · 0 = 0
0 · 3 = 0
Вывод: если любое число умножить на нуль или нуль умножить на любое число, значение произведения равно нулю.
Задание № 8 (с. 87).
– Прочитайте задание.
– Что известно в задаче? Что надо узнать?
– Выполните рисунок и ответьте на вопрос.
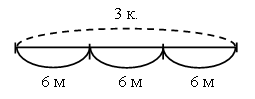
Решение: 6 + 6 + 6 = 18 (м).
6 · 3 = 18 (м).
Ответ: 18 метров.
Задание № 9 (с. 88).
– Прочитайте задачу.
– Что известно? Что требуется узнать?
– Составьте таблицу по условию задачи.
| Цена | Количество | Стоимость |
| 3 р. | 3 п. | ? р. |
| 5 п. | ? р. | |
| 7 п. | ? р. | |
| 9 п. | ? р. |
Решение:
1) 3 · 3 = 9 (р.) – стоимость 3 пакетиков.
2) 3 · 5 = 15 (р.) – стоимость 5 пакетиков.
3) 3 · 7 = 21 (р.) – стоимость 7 пакетиков.
4) 3 · 9 = 27 (р.) – стоимость 9 пакетиков.
V. Повторение пройденного материала.
1. Работа по учебнику.
Задание № 28 (с. 91).
– Какой многоугольник называется семиугольником? Назовите его признаки.
– Как построить семиугольник? (При построении многоугольника сначала отмечают его вершины (точки), а затем по линейке проводят стороны (отрезки).)
Задание № 29 (с. 91).
– Какая линия называется окружностью?
– Что такое радиус?
– Как построить окружность с заданным радиусом?
– Чему равен радиус второй окружности? (6 – 2 = 4 (см).)
Чертеж:

– Назовите точки пересечения данных окружностей. (Центр О.)
Задание № 30 (с. 91).
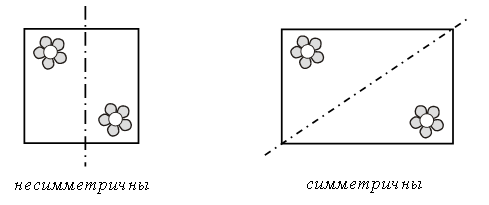
– Какие фигуры называются симметричными?
– Симметричны ли цветочки относительно линии сгиба?
– Проверьте свой ответ с помощью зеркала, которое нужно установить вертикально на линии сгиба каждого из платочков.
2. Работа в печатной тетради № 1.
Задание № 142.
– Рассмотрите чертеж. Что здесь изображено?
– Что такое числовой луч?
– Что называют координатой?
– Какую координату имеет точка А?
– Как отметить точку В?
– Как отметить точку С?
Решение:
Точка В расположена правее точки А и на расстоянии четырех единичных отрезков от нее. Следовательно, точка С должна быть левее точки А и находиться на расстоянии четырех единичных отрезков от нее.

Задание № 143.
– Чем окружность отличается от круга?
– Рассмотрите чертеж. Как расположены круг и окружность? Есть ли у них общая часть? (Общей частью окружности и круга является дуга окружности АВ.)