– Сегодня на уроке будем учиться изображать геометрическую фигуру луч с помощью линейки.
IV. Работа над новым материалом.
– Какую геометрическую фигуру называют лучом?
– Как обозначить луч на чертеже?
– Прочитайте названия лучей, данных на доске.

– Чем они похожи? Чем отличаются?
Задание № 4 (с. 18).
Чертеж:

Задание № 5 (с. 18).
– Рассмотрите чертежи.
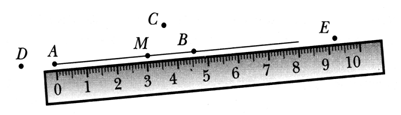
– Назовите геометрические фигуры, которые здесь изображены. (Точки, отрезок, лучи.)
– Назовите точки, которые лежат на луче АВ. (Точки А, М, В, Е.)
– Назовите точки, которые не лежат на этом луче. (D, C, F.)
Затруднение у учащихся могут вызвать точки D и Е. Учащиеся знают, что луч – бесконечная фигура, поэтому изобразить полностью любой луч на рисунке невозможно. Точка D расположена за началом луча, следовательно, не может лежать на луче. А вот для выяснения вопроса о том, лежит ли точка Е на луче, удобнее всего воспользоваться линейкой. Если расположить линейку так, как показано на рисунке, то становится видно, что точка Е лежит на луче.
Задание № 6 (с. 18).
Чертежи:

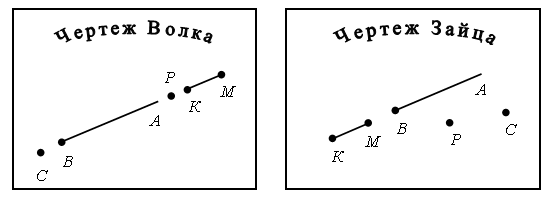
– Волк и Заяц тоже выполнили это задание. Рассмотрите их чертежи. Кто из них прав? Объясните свой ответ.
– Какие ошибки у них допущены?
V. Повторение пройденного материала.
1. Работа в печатной тетради № 1.
Задание № 23.
Направления движения Маши и Миши задаются лучами. Общее начало этих двух лучей изображено на рисунке точкой. Так как Маша и Миша пошли в противоположных направлениях, то дляпостроения сразу обоих лучей удобно линейку расположить так:

Задание № 25.
Скорее всего, дети предложат следующие решения:

| Отрезок АВ имеет с лучом ОМ единственную общую точку Е | Отрезок АВ имеет с лучом ОМ единственную общую точку А | Отрезок ОВ имеет с лучом ОМ единственную общую точку О |
Можно дать дополнительное задание, направленное на выявление глубины усвоения материала: «Волк и Заяц тоже выполнили это задание. Рассмотрите чертежи. Справились ли с заданием Волк и Заяц? Свой ответ поясните».

(Чертежи заранее делаются учителем.)
Если у учащихся правильно сформировано представление о луче, то они увидят, что с заданием справился только Заяц.
2. Работа по учебнику.
Задание № 13 (с. 20).
– Вспомните правила построения графа.
Решение:

Задание № 16 (с. 21).
– Прочитайте задачу.
– Что известно? Что требуется узнать?
– Как вы думаете, можно ли изменить условие задачи так, чтобы число 6 называлось только один раз?
Новая формулировка задачи: У Бори 6 простых и столько же цветных карандашей. Сколько карандашей у Бори?
– Запишите решение новой задачи.
Задание № 19 (с. 21).
– Прочитайте условие задачи.
– Что известно? Что требуется узнать?
– Используя цветные палочки, решите эту задачу.
Рассуждение: «По условию задачи Братец Кролик посадил 2 десятка семян моркови и 3 десятка семян редиса. Выложим с помощью цветных палочек эти числа:
| Морковь | Редис | ||||
| ор. | ор. | ор. | ор. | ор. | |
Так как в задаче спрашивается, сколько морковок и редисок надеется собрать Братец Кролик, надо сложить (сдвинуть на модели) эти числа:
| Всего | ||||
| ор. | ор. | ор. | ор. | ор. |
Получилось число, в котором 5 десятков (5 оранжевых палочек), – это 50. Значит, Братец Кролик надеется собрать 50 морковок и редисок».
В тетради запишем решение задачи:
20 + 30 = 50 (к.).
Ответ: 50 корнеплодов.
– Прочитайте еще раз вопрос задачи.
– Как вы думаете, почему в вопросе задачи используется слово «надеется»?
– Можем ли мы точно утверждать, что Братец Кролик осенью соберет ровно 50 морковок и редисок? Почему?
– Скорее всего, он соберет меньше 50 морковок и редисок или ровно 50?
– Можем ли мы точно утверждать, что Братец Кролик не соберет больше 50 морковок и редисок. Почему?






