Недостатком можно считать и сохранение вида распределения. Прийти к такому выводу довольно просто, если вспомнить о цели введения производных показателей, предназначенных для решения задачи сопоставимости результатов испытуемых по различным тестам. С точки зрения теории значения стандартных показателей сопоставимы только тогда, когда исходные распределения сырых баллов имеют приблизительно одну и ту же форму, как правило форму нормальной кривой. На практике ни одно из эмпирических распределений не является совершенно нормальным, а большинство распределений просто далеки от нормальной кривой. Поэтому желательным считается преобразование, не сохраняющее, а изменяющее вид распределения для приближения к виду нормальной кривой.
Удобным средством преодоления отмеченных затруднений является нелинейное преобразование, позволяющее придать эмпирическому распределению желаемую форму нормальной кривой. С этой целью вводятся нормализованные стандартные показатели, соответствующие распределению, преобразованному так, что оно аппроксимируется формой нормальной кривой. Их значения могут быть найдены с помощью специальных таблиц, в которых приводится процент случаев различных отклонений в единицах от среднего значения для нормальной кривой.
Сначала для каждого сырого показателя определяется кумули-рованная частота как сумма всех частот, лежащих ниже данного сырого показателя. Затем к ней добавляется половина количества испытуемых, имеющих данный сырой балл. По этим данным вычисляется кумулированная доля путем деления полученной суммы на общее число испытуемых выборки. По статистическим таблицам (например, Fisher R. А., Yates. Statistical Tables for Biological and Medical Research), содержащим значения площади под кривой нормального распределения, находят значения нормализованных стандартных показателей для каждой кумулированной доли.
Нормализованный стандартный показатель, как и линейно преобразованный стандартный показатель, имеет среднее значение Q, если сырой балл приходится на самую середину нормальной кривой, т. е. не превышает 50% результатов группы. Результат — 1 можно интерпретировать как превышающий приблизительно 16% результатов группы, а +1 — как превышающий 84% всех результатов.
ШКАЛЫ СТАНАЙНОВ И СТЕНОВ
Нормализованным стандартным показателям стараются придать удобную форму, пригодную для сообщения результатов. Для этого используют шкалы стандартных 10 или 9 единиц. Разбиение нормального распределения на 9 интервалов приводит к шкале станайнов, имеющей 9 стандартных единиц. При оценке результатов испытуемых по любому тесту с любым числом заданий 4% самых худших результатов присваивается станайн 1, а самых лучших—станайн 9. Следующим за худшими и лучшими 7% результатов присваивают станайны 2 и 8 соответственно. Следующим за ними 12% результатов — станайны 3 и 7. Следующим 17% присваивают станайны 4 и 6 и, наконец, 20% средних результатов соответствует станайн 5.
В дополнение к описанной шкале станаинов есть еще две шкалы, имеющие некоторое преимущество перед девятибалльной шкалой в плане различающей способности. Одна из них — шкала стандартных 10 единиц, называемая часто шкалой Кэттела или шкалой стенов (sten). Как следует из названия, весь массив результатов делится на 10 частей с интервалом 0,5 стандартного отклонения. В шкале стенов среднее арифметическое принимается равным 5,5, а расстояние между двумя соседними стандартными единицами равно 0,5 s.
ОДИННАДЦАТИБАЛЛЬНАЯ ШКАЛА
Выявить по одному проценту самых сильных и самых слабых испытуемых и присвоить им соответственно максимальный и минимальный баллы можно, удлинив шкалу станаинов путем добавления по одному интервалу в 0,55 справа и слева. Таким образом получают одиннадцатибалльную шкалу.
Если значениям стандартных баллов поставить в соответствие оценочные эквиваленты, то соотношение между значениями стандартных Z-оценок, процентом испытуемых, оценочными эквивалентами и баллами испытуемых можно представить в виде табл. 7.7.
В большинстве учебных заведений нашей страны обычно пользуются пятибалльной шкалой, что хотя и часто критикуется, однако не меняется на протяжении многих десятилетий. Переход в пятибалльную шкалу снимает возможность тонкой дифференциации испытуемых, тем самым теряется важнейшее преимущество педагогических тестов.
В процессе перехода от нормализованных стандартных показателей к традиционным баллам возникают определенные трудно-
Таблица 7.7. Соотношение между баллами, оценочными эквивалентами, Z -оценками и процентом испытуемых
| Баллы, пятибалльная шкала | Баллы, одиннадцатибалльная шкала | Оценочный эквивалент | /Г-оценка | Процент испытуемых | Станайн |
| 2 | 1 | Низшая оценка | Z<-2,25 | 1 | |
| 2 | Неудовлетворительно | -2,25 <Z< -1,75 | 3 | 1 | |
| 3 | 3 | Малоудовлетворительно | . -1,75 <.Z< -1,25 | 7 | 2 |
| 4 | Удовлетворительно | -1,25 <Z< -0,75 | 12 | 3 | |
| 5 | Ниже среднего | -0,75 <Z< -0,25 | 17 | 4 | |
| 4 | 6 | Среднее | -0,25 <Z< 0,25 | 20 | 5 |
| 7 | Выше среднего | 0,25 <Z< 0,75 | 17 | 6 | |
| 8 | Хорошо | 0,75 <Z< 1,25 | 12 | 7 | |
| 5 | 9 | Очень хорошо | 1,25 <Z< 1,75 | 7 | 8 |
| 10 | Отлично | 1,75<Z<2,25 | 3 | 9 | |
| 11 | Высшая оценка | 2,25 < Z | 1 |
сти, связанные с необходимостью огрубления результатов. В частности, приходится принимать решения относительно испытуемых, чьи результаты принадлежат интервалу-1,75 < Z< -1,25, поскольку их можно отнести как к неудовлетворительно, так и к удовлетворительно выполнившим тест.
Аналогичные трудности возникают с тестовыми баллами испытуемых из интервала -1,25 < Z< -1,25. В пятибалльной шкале их результаты можно оценить как четырьмя, так и пятью баллами. При этом приходится помнить, что полученные границы интервалов являются теоретическими. Фактически же они могут слегка сдвигаться в ту или иную сторону, поскольку длина их зависит от величины стандартной ошибки измерения. Например, если Z-оценка испытуемого равна 1,25, то истинное значение его балла может быть больше или меньше этого числа на значение ошибки. Таким образом, можно отнести к категории ответивших хорошо и оценить четырьмя баллами испытуемого с истинным баллом большим 1,25.
Введение одиннадцатибалльной шкалы в качестве общепринятой вместо пятибалльной может дать ряд преимуществ, связанных с повышением дифференцирующей способности педагогической оценки более чем в 2 раза. Особенно четко в одиннадцатибалльной шкале дифференцируется 1 % лучших и худших испытуемых. Определенное преимущество психологического характера есть у одиннадцатибалльной шкалы и по сравнению с девяти- и десятибалльной шкалами. Оно связано с тем, что в качестве опорных точек шкалы используются привычные для обучаемых понятия: низшая оценка — балл 1, средний уровень — балл 6, высшая оценка — балл 11.
В заключение хотелось бы отметить, что в практике деятельности различных тестовых центров встречаются попытки оценки знаний по сильно растянутой, например по двадцатибалльной, стобалльной или даже тысячебалльной шкале. Однако такие попытки следует признать не очень удачными, так как они находятся в противоречии с ограниченными психологическими возможностями человека, которому трудно определить место своего результата на столь широком диапазоне и отнести его тем самым к категории плохих или хороших.
Как правило, используемые в процессе преобразования Z-показателей новые значения среднего и стандартного отклонения выбирают из соображений удобства. Особенно удобны Z-показатели в том случае, если распределение сырых баллов можно аппроксимировать нормальной кривой, поскольку пропорции между площадями различных сегментов поднормальной кривой известны. Следовательно, Z-показатели легко преобразовать в проценты и проинтерпретировать в терминах процентилей.
Однако к такой интерпретации нужно относиться с определенной осторожностью, если сравниваются результаты, полученные на различных выборках по нескольким тестам. Например, нельзя делать вывод, что процентильный ранг 84 по одному тесту обязательно эквивалентен Z-оценке +1,0 по другому тесту. Этот вывод может иметь место лишь в том случае, когда каждый тест обеспечивает нормальное распределение сырых баллов и обе шкалы основаны на одинаковых или очень похожих выборках людей (Test Service Bulletin, № 48).
Возможность искусственной нормализации любого распределения сырых баллов некоторыми исследователями подвергается вполне обоснованному сомнению, поскольку зачастую нормализация приводит к неизбежным искажениям исходного распределения. Поэтому нормализованные стандартные показатели рекомендуется использовать лишь в том случае, когда исходное распределение близко к нормальному и для предположения о близости есть веские теоретические основания. Во всех остальных случаях предпочтение следует отдать стандартным показателям, основанным на вычислении отклонения сырых баллов от среднего. Стандартные показатели, подвергнутые линейному преобразованию в единую шкалу с удобными значениями среднего и стандартного отклонения, обеспечивают сравнимость результатов, полученных испытуемыми по различным тестам. Одинаковые стандартные показатели находятся на одинаковом расстоянии от среднего.
Хотелось бы также отметить некоторую терминологическую путаницу, встречающуюся в переводах на русский язык англоязычной литературы по тестовой проблематике. В ряде изданий термины «нормализованные стандартные» оценки и «нормальные стандартизованные» оценки используются как рядоположенные, хотя для этого нет никаких оснований. Вследствие преобразования сырых баллов в Z-шкалу получаются стандартные оценки, которые в отдельных случаях подвергаются нормализации. В то время как термин «нормальные стандартизованные» оценки используется в ряде других случаев, не имеющих отношения к вопросам шкалирования.
При построении шкалы по тесту возникают определенные проблемы, связанные с ее устойчивостью, если тест используется в различное время учебного года либо выполняется испытуемыми различных возрастных групп. Однако и в этих случаях можно предпринять определенные шаги, способствующие повышению устойчивости тестовых шкал. При этом необходимо предположить, что приращение оцениваемого уровня подготовки по предмету происходит равномерно на протяжении всего времени изучения предмета. В качестве таких шагов при конструировании шкалы Торндайк предложил следующие [48]:
• получить репрезентативную выборку испытуемых для вычисления устойчивых оценок уровня знаний с известными стандартными ошибками измерения;
• предъявить тест выборке подходящего возраста и периода обучения, объединив испытуемых выборки в одинаковые возрастные группы и разбив на трехмесячные подгруппы по периодам обучения;
• определить средний балл для каждой подгруппы, шкалировать результаты;
• интерполировать шкалированные результаты между соседними средними для тех сырых баллов, которые не наблюдались в выборке;
• экстраполировать результаты с учетом минимального и максимального наблюдаемых баллов для установления возможных границ шкалы по тесту;
• результаты интерполяции и экстраполяции собрать в таблицу, указывающую шкалированные эквиваленты сырых баллов в различных возрастных подгруппах или с учетом определенного периода обучения.
Шкала логитов
Зарубежные исследования конца 80-х годов показали плодотворность шкалирования тестовых результатов испытуемых посредством использования математических моделей, разработанных в рамках IRT. Согласно основным положениям IRT, уровень подготовки испытуемых и трудность заданий теста считаются некоторыми латентными параметрами, оценки которых предстоит получить в процессе шкалирования результатов выполнения теста. При этом предполагается, что вероятность правильного ответа определяется значениями двух латентных параметров, один из которых — уровень подготовки испытуемых, а второй — трудность заданий теста. Зависимость между вероятностью правильного ответа и значениями параметров выражается с помощью ряда математических моделей, предполагающих введение единой шкалы как для уровня знаний испытуемых, так и для трудности заданий теста (см. разд. 5.3).
Таким образом, латентные оценки параметров испытуемых и заданий располагаются вдоль одной шкалы логитов. Благодаря этому каждую точку шкалы, соответствующую оценке уровня подготовки испытуемого, можно соотнести с трудностью заданий, лежащих на шкале логитов левее и правее этой точки. Пример подобного соотнесения показан на рис. 7.3.

Рис. 7.3. Графическая интерпретация распределения
Точками pj, Р2,... на шкале логитов отмечены значения, соответствующие трудности теста, причем pt < Р2 < р3 <..., т. е. задания расположены по нарастанию трудности на всем протяжении теста. Точки 0р 02,... соответствуют уровням подготовки подгрупп испытуемых, а высота столбиков пропорциональна количеству испытуемых, обладающих одинаковым уровнем подготовки в каждой подгруппе.
Расположение значений параметров 0 и р на одной оси позволяет провести интересную геометрическую интерпретацию. Любой испытуемый группы в состоянии выполнить с вероятностью больше 0,5 все задания, лежащие на оси левее точки, соответствующей оценке его уровня подготовки. И наоборот, вероятность правильного выполнения всех заданий, расположенных правее этой точки, меньше 0,5. Например, три испытуемых с уровнем подготовки 06 наверняка смогут выполнить верно 1-е, 2-е и 3-е задания теста. Вероятность правильного выполнения 4-го задания для трех испытуемых этой подгруппы немногим больше 0,5. А вот задания с трудностью Р7 и Р8 для этих трех учеников явно слишком сложные.
Как следует из результатов разд. 5.3, наиболее эффективными для тестирования испытуемых с уровнем подготовки 9 являются задания с трудностью р ~ 0. Опираясь на это правило подбора заданий в тест, удобно визуально с помощью рисунка оценить эффективность создаваемого теста. В том случае, когда большая часть заданий теста расположена на шкале логитов значительно левее или правее множества значений 0, как, например, в случаях А и Б, рис. 7.4, тест не годится для оценки знаний рассматриваемого контингента учеников.
Совсем иначе обстоит дело в случае В, когда основная часть заданий расположена на оси логитов именно там, где находится множество параметра 0 для тестируемой группы учеников. В последнем случае тест явно удался, так как по подбору трудности заданий рассчитан на тестируемую группу.
Так как матрица тестовых результатов дает наблюдаемые, сырые значения тестовых баллов, а не оценки латентных параметров испытуемых и заданий в логитах, то необходимы специальные алгоритмы вычисления параметров 9 и b, подобные тем, которые были подробно рассмотрены в гл. 5.
Условно процесс шкалирования можно подразделить на три этапа. Первый предполагает построение шкалы логитов уровня знаний, второй — шкалы логитов трудности заданий и третий этап позволяет свести две шкалы в общую шкалу стандартных оценок для уровня подготовки испытуемых и трудности заданий теста.
Процедура построения шкалы латентных переменных связана с процедурой шкалирования по Гуттману [47], когда задания отбираются в порядке нарастания их трудности по определенным, тщательно структурированным элементам содержания дисциплины. При этом предполагается, что любой испытуемый с правильной структурой знаний, справившийся с каким-либо заданием, может успешно выполнить все предыдущие, более легкие задания теста. Это предположение чаще всего не выполняется, как правило, по причине неудачно сделанного теста. Если тест разработан профессионально, то каждый профиль ответов испытуемого будет характеризовать ту или иную структуру знаний испытуемого и в совокупности с тестовым баллом определять качество его знаний. Это обстоятельство делает чрезвычайно привлекательной шкалу Гуттмана для педагогов, хотя ее довольно редко удается реализовать в практике.
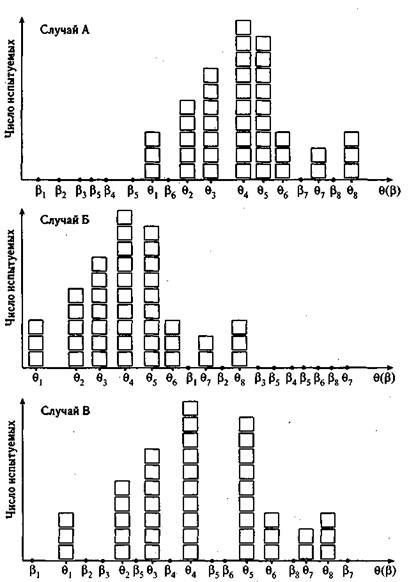
Рис. 7.4. Визуальная оценка эффективности теста
Шкалирование по алгоритмам IRT в определенной степени преодолевает трудности построения шкалы Гуттмана, поскольку является ее вероятностной версией и отражает вероятностную сущность тестовых процессов. Согласно модели Г. Раша, о правильном выполнении любого задания /-м испытуемым можно говорить лишь с некоторой вероятностью и прогнозировать успешность лишь в том случае, если эта вероятность больше 0,5.
Единая шкала, содержащая новые единицы измерения, называемые логитами, позволяет реализовать преимущества математических моделей теории IRT. Первое преимущество вытекает из стандартизованного характера оценок параметров испытуемых и заданий в шкале логитов. Как и любые стандартизованные величины, оценки латентных параметров представляют собой результат преобразования исходных сырых оценок разного происхождения в единую интервальную шкалу. Это дает возможность объективного сравнения достижений испытуемых по различным предметам, что, конечно, особенно важно в процессе экзаменов.
Второе преимущество связано с введением единицы измерения, позволяющей измерять в единой шкале уровень подготовки испытуемых и трудность заданий теста. В отличие от стандартных шкал (типа Z-шкалы, Т-шкалы и им подобных) шкала латентных переменных является интервальной. Равные приращения сырых баллов испытуемых не соответствуют равным приращениям шкалированных оценок латентных параметров, зато последние разности приобретают вполне интерпретируемый смысл, поскольку их можно считать мерой отличия уровня подготовки испытуемых по предмету.
Третье преимущество вытекает из специфических особенностей математических моделей, используемых для оценоклатентных параметров испытуемых и заданий. Получаемые с их помощью статистические оценки параметров обладают относительной независимостью друг от друга, хотя ряд авторов (Лорд (Lord), Чопин (Chopin) [11]) считают такое утверждение явным преувеличением.
Возможна эмпирическая проверка этого утверждения, которая должна быть разбита на два этапа. Первый этап — проверка независимости оценок латентного параметра трудности заданий от уровня подготовленности тестируемой выборки — включает ряд шагов. В результате их выполнения удается отобрать задания, удовлетворяющие выдвинутому предположению о существовании такой независимости.
Второй этап, гораздо более важный, посвящен проверке инвариантности оценок латентного параметра испытуемых относительно различных наборов заданий, отобранных на первом этапе, и состоит из нескольких шагов. На первом шаге все задания, прошедшие проверку, делятся на две группы: одна содержит самые легкие, а другая — наиболее трудные задания теста. На втором шаге вычисляются оценки латентных параметров испытуемых по каждой из двух групп заданий и связанные, с ними стандартные ошибки измерения. Если задания удовлетворяют требованиям моделей латентно-структурного анализа и прошли первый этап, то с точки зрения теории оценки параметра испытуемых в пределах стандартной погрешности должны быть примерно одинаковыми как по группе самых легких, так и по группе самых трудных заданий теста. Однако на практике это выполняется далеко не всегда.
Нередко наблюдаемые существенные отклонения в оценках испытуемых указывают на необходимость удаления или пере формулировки прошедших первый этап отбора заданий теста. Однако следует иметь в виду, что для выводов о наличии инвариантности или об отсутствие ее одной выборки испытуемых недостаточно. Работу по шкалированию можно считать завершенной, если эффект инвариантности обретает характер стабильности и наблюдается на различных выборках каждый раз.
В некоторых случаях эффект инвариантности может быть искажен угадыванием ответов, плохой формулировкой дистракторов либо отсутствием внутренней согласованности заданий теста. Проверка внутренней согласованности заданий осуществляется специальной процедурой, получившей название Within population item-fit, и проводится после оценивания латентных параметров [59]. По результатам проверки выбраковываются эмпирические данные тестирования, не удовлетворяющие требованиям моделей измерения. Оставшиеся задания дают основания для построения одномерной шкалы латентных параметров или в традиционной терминологии являются внутренне согласованными, однородными, удовлетворяющими задаче создания гомогенного теста. Таким образом, возможность получения независимых оценок латентных параметров устанавливается путем двухэтапного исследования и в случае необходимости достигается с помощью специальной процедуры подгонки эмпирических данных тестирования под требования модели. При этом часто как-то забывается, что этап работы над заданиями, их отбор, шкалирование и переформулировка являются первичными, поскольку качество заданий определяет качество оценок испытуемых, полученных с помощью теста. Если этот этап не пройден, то никогда не может быть достигнута инвариантность оценок испытуемых от трудности заданий теста, т. е. не будет реализовано важнейшее преимущество математических моделей теории латентно-структурного анализа.
Четвертым преимуществом рассматриваемых моделей является устойчивость оценок латентных параметров, основанная на их относительной независимости друг от друга. Хотя о полной независимости оценок говорить, конечно, нельзя, но все же оценки параметров в шкале логитов имеют тенденцию к стабилизации, что, несомненно, делает эту шкалу наиболее привлекательной на всем множестве шкал тестовых измерений.
Помимо достоинств, у шкалы логитов есть и определенный недостаток. Поскольку оценки параметров обычно лежат в интервале (—5; 5) и имеют несколько знаков после запятой, они малопригодны для сообщения испытуемым. Преподаватели-практики, как правило, категорически возражают против применения отрицательных дробных значений параметра для оценки уровня подготовки учеников. По этой причине возникает необходимость преобразования оценок в другую, более удобную для сообщения результатов шкалу.






