Последнее задание скорее похоже на вариант со свободно конструируемым ответом, чем на задание с ограничениями, в котором невозможны различные продолжения, приводящие к логически несоразмерным, подобранным по разным основаниям ответам. Конечно, при использовании подобного задания в тесте у преподавателей всегда возникают проблемы с оценкой результатов учеников.
Возможны ситуации, когда ответы в большинстве своем будут отличаться от планируемого эталона, но незначительно, поэтому их нельзя оценить как полностью неправильные. К тому же в ситуации неопределенности здесь виноват разработчик, а неконтролируемый ученик. Для коррекции задания в его текст необходимо внести уточнения, связанные с сужением объема проверяемого понятия и уменьшением за счет этого количества дополняемых слов в ответе. В результате подобных уточнений разработчик, несомненно, добьется ясности смыслового содержания заданий, но проиграет в краткости. Однако это неизбежно, поскольку каждое задание на дополнение 'с ограничениями с необходимостью должно порождать единственный правильный ответ.
Несмотря на видимые преимущества по сравнению с закрытой формой, основной сферой применения заданий на дополнение остается текущий контроль. Реже они используются в итоговом контроле из-за трудностей с проверкой, которая становится крайне трудоемкой, довольно субъективной и требует привлечения большого количества педагогов в случаях массового тестирования учеников.
Задания на установление соответствия
В заданиях на соответствие преподаватель проверяет знание связей между элементами двух множеств. Слева обычно приводятся элементы задающего множества, содержащие постановку проблемы. Справа — элементы, подлежащие выбору, хотя возможно и иное расположение, как, например, в книге [43].
К заданиям прилагается стандартная инструкция, состоящая из двух слов: установите соответствие.
Например:
УСТАНОВИТЕ СООТВЕТСТВИЕ
| Назначение |
Задание 1
Название
1. Простая функция
аргументах
2. Сложная функция
аргументах
3. Неявная функция
4. Параметрически
заданная функция
Ответы: 1_, 2__, 3__, 4__
|
|
| Ответы: 1) _, 2)_, 3)_, 4)_ |
Задание 2
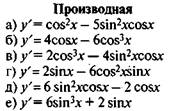
Задание 3
Для случая, если радиус-вектор частицы определяется выражени ем 
Характеристики Их числовое значение
1) путь частицы
за первые 2 с, м а) 20
2) модуль перемещения ' б) 500
за первые Юс, м в) 10
3) модуль скорости частицы г) 40
в момент времени/=1с,м/с д)300
Ответы:!)__, 2)__, 3)_
Задание 4








