При поступательном движении твердого тела все его точки движутся также как центр масс. Поэтому поступательное движение тела сводится к движению любой его точки, и дифференциальными уравнениями поступательного движения будут являться проекции теоремы о движении центра масс на оси координат, где произвольной точкой будет центр масс.
. (10.1)
Дифференциальное уравнение вращательного движения твердого тела вокруг неподвижной оси имеет вид:
(10.2)
Произведение углового ускорения тела на осевой момент инерции равно сумме моментов внешних сил относительно оси вращения.
Дифференциальные уравнения плоского (плоскопараллельного) движения твердого тела может быть представлено как поступательное движение вместе с центром масс и вращательное движение вокруг оси ОZ:
(10.3)
IZc –момент инерции тела относительно оси, перпендикулярной плоскости движения и проходящей через центр масс.
Примеры решения задач
Задача 1
Определить радиус инерции шкива, масса которого m = 50 кг и радиус R = 0,5 м, если под действием силы натяжения троса Т = 18t он вращается вокруг оси Oz по закону φ = t 3 / 3 + 3 t.
Решение
Используем дифференциальное уравнение вращательного движения тел:
где 
– момент силы Т относительно оси OZ.
– кинетический момент шкива.
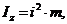
Ответ: 
Задача 2
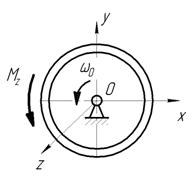
На какой угол повернется за 1 с маховик, масса которого m = 1,5 кг и радиус инерции i = 0,1 м, если он начинает вращаться из состояния покоя под действием главного момента внешних сил M E Z = 0,15 
?
Решение
Используем дифференциальное уравнение вращательного движения тел: 
.
, 
,
; 
, 
, 
, 
,
, 
, 
, 
, 
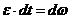рад.
Ответ: 
рад.
Работа силы
В общем случае работа силы на конечном перемещении 
равна
. (11.1)
Данная формула является наиболее общей для вычисления работы силы на конечном перемещении. Она применяется в следующих случаях:
1) когда точка под действием силы перемещается по криволинейной траектории;
2) когда точка перемещается по прямой, но сила переменна по величине и/или по направлению.
Работа A постоянной по модулю и направлению силы 
, действующей на прямолинейном перемещении 
материальной точки, есть произведение модуля F силы, модуля s перемещения и косинуса угла a между векторами силы и перемещения.
. (11.2)
Единицей измерения работы в системе СИ является 1 Джоуль (1 Дж).
Работа силы тяжести
A = ± m × g × h (11.3)
Работа силы упругости
, (11.4)
где h – деформация пружины.
Работа момента силы
. (11.5)
Если момент 
, то последняя формула примет вид
(11.6)
Примеры решения задач
Задача 1
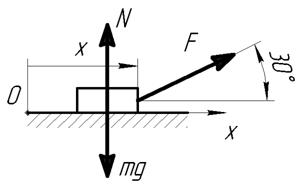
На тело действует постоянная по направлению сила 
. Определить работу этой силы при перемещении тела из положения с координатой x 0 = 0 в положение с координатой x 1 = 1 м.
Решение
Работа силы определяется по формуле:
, 
,
, 
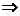
Дж.
Ответ: 
Дж.
Задача 2
Цилиндр, масса которого m = 1 кг, радиус r = 0,173 м, катится без скольжения. Определить суммарную работу силы тяжести и силы сопротивления качению, если ось цилиндра переместилась на расстояние s = 1 м и коэффициент трения качения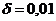 
м.
Решение
– работа силы тяжести
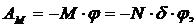– Работа момента силы сопротивления M.
Спроецируем все силы на ось OY:
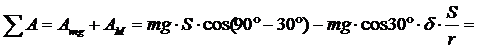
Ответ: 
