Механическая система – любая совокупность взаимосвязанных между собой материальных точек. Действующие на механическую систему силы подразделяются на внешние (
) и внутренние (
), активные (
) и реакции связей (
).
Внешние силы – силы, действующие на точки (тела) механической системы со стороны точек (тел), не входящих в данную механическую систему. Внутренние силы – это силы взаимодействия между материальными точками (телами) самой механической системы.
В силу третьего закона Ньютона главный вектор и главный момент внутренних сил относительно произвольной точки O равны 0.
; 
, (5.1)
Несмотря на это, движение системы происходит под действием внешних и внутренних сил.
Центром масс или центром инерции механической системы называется геометрическая точка, положение которой определяется радиусом-вектором:
, (5.2)
, 
, 
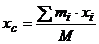, (5.3)
где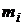 
– масса i -й материальной точки системы; 
– радиус-вектор этой точки; 
, 
и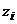 
– координаты точки, 
– масса всей системы.
Теорема о движении центра масс звучит следующим образом: центр масс механической системы движется как материальная точка с массой равной массе всей системы, к которой приложены все внешние силы действующие на систему.
. (5.4)
Из теоремы о движении центра масс механической системы следует, что движение всей механической системы можно рассматривать как движение одной точки – центра масс
Используя вышеописанные уравнения можно определять движение центра масс системы, не определяя движения отдельных ее точек.
Примеры решения задач
Задача 1
Тело 1 массой m 1 = 4 кг может двигаться по горизонтальной направляющей. На какое расстояние переместится тело 1, когда однородный стержень 2 массой m 2 = 2 кг и длиной l = 0,6 м, опускаясь под действием силы тяжести, займет вертикальное положение. В начальный момент система находилась в покое.
Решение
Выберем начало системы отсчета. Расстояние от оси Y до центра масс 1 тела обозначим X 1, а до тела 2 X2. Предположим, что при перемещениитела 2 в вертикальное положение вся система сместится вправо на расстояние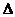 
согласно теореме о сохранении положения центра масс. Координата центра масс первого тела будет равна 
, а второго тела 
.
Запишем уравнение для определения центра масс всей системы для 1-го и 2-го положений.
; 
;
Т.к. 
, 
,
; 
;
; 
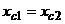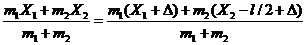м.
Ответ: 
м.
Задача 2
Тело 1 массой m 1 = 0,7 кг может двигаться по горизонтальной направляющей. Определить ускорение тела 1 в момент времени t = 0,25 с, если относительно негопод действием внутренних сил системы движется тело 2 массой m 2 = 0,1 кг согласно уравнению 
.
Решение
Выберем начало системы отсчета. Расстояние от оси Y до центра масс 1 тела обозначим X 1, а до тела 2 X 2. При перемещениитела 2 в нижнее положение вся система должна сместиться вправо на расстояние 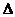согласно теоремы о сохранении центра масс. Координата центра масс первого тела будет равна , а второго тела 
.
Запишем уравнение для определения центра масс всей системы в 1-ом и 2-ом положениях.
; 
;
т.к. ,
,
;
;
; 
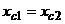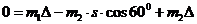м.
Для определения ускорения 1-го тела необходимо дважды продифференцировать полученную зависимость:
; 
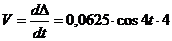м/с2.
Ответ: 
м/с2.
