На развитие явления или процесса во времени могут оказывать влияние различные по своему характеру и силе воздействия факторы. Одни из них действуют более или менее постоянно и формируют в рядах динамики определённую тенденцию, а другие действуют случайно, кратковременно.
Для изучения в рядах динамики общей тенденции используют следующие приёмы и методы:
1) Метод укрупнения интервалов основан на укрупнении периода времени, к которому относятся уровни ряда динамики (например, укрупнение квартальных уровней до годовых, уровней за месяц до уровней за квартал и т.д.). Общий итог показателя укрупнения периодов времени можно получить лишь для абсолютных значений уровней интервальных рядов. Для рядов средних величин вычисляются лишь новые средние уровни.
Пример:
| 2004г. | I | II | III | IV | 2005г. | I | II | III | IV |
| Товарная продукция, млн. руб. | 15 | 10 | 14 | 17 | 16 | 12 | 15 | 18 |
 56 61
56 61
2)Метод скользящей (подвижной) средней состоит в том, что абсолютные данные заменяются средними арифметическими простыми за определённые периоды времени, и эти средние относятся к середине интервала, по которому ведётся расчёт. Средние вычисляются способом скольжения, т.е. из принятого периода скольжения постепенно исключается первый уровень и включается последующий.
Если число уровней ряда в скользящей средней чётное, то рассчитываемая средняя попадает между двумя временны́ми точками – уровнями ряда. Для ликвидации этого смещения применяют центрирование и в этом случае из каждой пары рядом стоящих скользящих средних рассчитывается средняя арифметическая, которая и относится теперь уже к определённой временно́й точке.
Недостаток метода заключается в том, что сглаженный ряд укорачивается по сравнению с исходным рядом динамики. Если необходимо сгладить мелкие беспорядочные колебания, то интервал сглаживания берут по возможности большим, и, наоборот, интервал сглаживания уменьшают, когда нужно сохранить более мелкие волны и освободиться от периодически повторяющихся колебаний.
Пример:
имеется исходный ряд динамики:
15 10 14 17 16 12 15 18
Определяем основную тенденцию с помощью скользящей средней из 3-х уровней ряда и рассчитываем скользящие средние:

Результаты расчётов запишем в таблицу:
| у | 
| 
| 
| ||
| 15 | – | 
| – | ||
| 10 |
| – | |||
| 14 | 13,7 | 14,13 | |||
| 17 | 15,7 | 14,5 | |||
| 16 | 15,0 | 14,9 | |||
| 12 | 14,3 | 15,13 | |||
| 15 | 15,0 | – | |||
| 18 | – | – |
Определяем теперь тенденцию с помощью скользящей средней из 4-х уровней ряда:
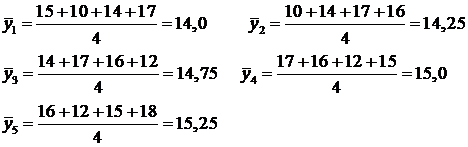
1) Более совершенный способ выравнивания рядов динамики – это аналитическое выравнивание, когда на основе фактических данных ряда динамики подбирается наиболее подходящяя математическая формула (аппроксимирующая функция) («аппроксимация» – приближение)  («игрек, выравненное по t»). Аналитическое выравнивание может быть произведено по:
(«игрек, выравненное по t»). Аналитическое выравнивание может быть произведено по:
P прямой  ;
;
P параболе второго порядка  и т.д.,
и т.д.,
где 
 – параметры уравнения; t – время (фактор времени).
– параметры уравнения; t – время (фактор времени).
Рассмотрим выравнивание по прямой; оно используется в тех случаях, когда абсолютные цепные приросты более или менее постоянны, т.е. значения уровней ряда изменяются в арифметической прогрессии или близко к ней.
Параметры а0 и а1 находятся с помощью метода наименьших квадратов путём решения системы уравнений:


Условия экстремума (минимума) функции: 
Получаем систему уравнений:
 или после преобразования:
или после преобразования:
 ,
,
где y – исходные уровни ряда динамики; n – число уровней ряда.
Расчёт параметров можно упростить, если отсчёт времени вести от середины ряда, при этом  .
.
При нечётном числе уровней ряда в серединной точке t принимается равным 0, для предшествующих периодов t = -1, -2 и т.д., а для последующих t = +1, +2 и т.д.; счёт времени при этом ведётся годами (месяцами). При чётном числе уровней ряда два серединных уровня имеют значения t = +1 и t = –1, а все остальные t обозначаются: +3, +5 и т.д., и, соответственно, –3, –5 и т.д., т.е. счёт времени ведётся полугодиями (полумесяцами).
| Год | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 |
| у | y1 | y2 | y3 | y4 | y5 | |
| t |  - 2 - 2
| 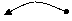 - 1 - 1
|  0 0
|  + 1 + 1
| + 2 | |
| y | y1 | y2 | y3 | y4 | y5 | y6 |
| t |  - 5 - 5
|   - 3 - 3
|   - 1 - 1
|   + 1 + 1
|   + 3 + 3
|  + 5 + 5
|
|
Тогда уравнения принимают вид:
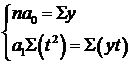 , откуда
, откуда 
Пример:
| y | 15 | 10 | 14 | 17 | 16 | 12 | 15 | 18 | 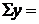 117 117
|
| t | -7 | -5 | -3 | -1 | +1 | +3 | +5 | +7 | 
|
| yt | -105 | -50 | -42 | -17 | +16 | +36 | +75 | +126 | 
|
| yt | 13,0 | 13,5 | 13,9 | 14,4 | 14,9 | 15,3 | 15,8 | 16,2 | 
|








