Кубанский государственный университет
Кафедра экономического анализа, статистики и финансов
Методический материал
По дисциплине
«Теория статистики»
Составитель – к.э.н., доцент Бабенко И.В.
Краснодар 2018
ТЕМА 1 «Статистическое изучение вариационных рядов»
Общие сведения о вариационных рядах, их построение
Статистические ряды подразделяются на два вида: ряды распределения и ряды динамики.
Ряды распределения представляют собой ряды чисел, характеризующих состав или структуру какого-либо явления или процесса после группировки статистических данных. Ряды распределения подразделяются на атрибутивные и вариационные. Вариационные ряды, в свою очередь, могут быть дискретными и интервальными. В дискретном ряду группировочный признак изменяется прерывно, как правило, целыми числами.
В интервальном ряду группировочный признак принимает любые числовые значения в пределах интервала. Интервалы, в свою очередь, могут быть равновеликими и неравновеликими.
Вариационный ряд представляет собой две строки (или две колонки), в одной из которых приводятся отдельные значения варьирующего признака, которые называются вариантами и обозначаются символом x, а в другой строке – абсолютные числа, показывающие, сколько раз встречается тот или иной вариант. Эти показатели второй строки (колонки) называются частотами и обозначаются обычно через m(f).
Во второй строке могут использоваться и относительные показатели, характеризующие долю частоты отдельных вариантов в общей сумме частот. Их именуют частостями и обозначают w  . Сумма всех частостей равна 1 (или 100%).
. Сумма всех частостей равна 1 (или 100%).
Пример атрибутивного ряда:
Крупнейшие производители мобильных телефонов в 2012 г., доля на мировом рынке в процентах
| Samsung | Nokia | Apple | ZTE | LG | Прочие | Итого |
| 23,7 | 19,6 | 8,0 | 3,8 | 3,3 | 41,6 | 100 |
Несгруппированные данные:
Ежедневный товарооборот, тыс. руб. (Величина уплаченных штрафов)
20 20 15 20 17 18 23 20 24 25 17
Дискретный вариационный ряд:
| x | 15 | 17 | 18 | 20 | 23 | 24 | 25 | Итого |
| m | 1 | 2 | 1 | 4 | 1 | 1 | 1 | 11 |
| S | 1 | 1+2=3 | 3+1=4 | 4+4=8 | 8+1=9 | 9+1=10 | 10+1=11 | – |
Интервальный вариационный ряд (равновеликий):
| x | 13-15 | 16-18 | 19-21 | 22-24 | свыше 24 | Итого |
| m | 1 | 3 | 4 | 2 | 1 | 11 |
| w |  (9%)
(9%)
|  (27%)
(27%)
|  (37%)
(37%)
| 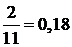 (18%)
(18%)
|  (9%)
(9%)
| 1,00 (100%) |
Для целых чисел признака границы интервалов могут не пересекаться, а для дробных – пересекаются во всех случаях.
Основные характеристики вариационного ряда
Средняя арифметическая. Для несгруппированных данных средняя арифметическая рассчитывается по формуле:
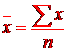 , где n – число значений признака (вариантов)
, где n – число значений признака (вариантов)
и называется средней арифметической простой.
Для дискретного вариационного ряда (где данные уже сгруппированы) рассчитывается средняя арифметическая взвешенная:
 , где m, f – веса.
, где m, f – веса.
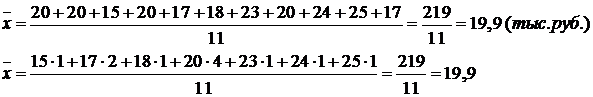
Понятие «вес» не всегда связано с подсчётом частот вариантов, и, следовательно, с вариационными рядами.
Для интервального вариационного ряда для исчисления  предварительно в каждом интервале определяется его середина, которая принимается за конкретное значение признака и умножается на соответствующую частоту. Середина интервала определяется как полусумма нижней и верхней границ интервала. Если у первого интервала нет нижней границы, а у последнего – верхней, то эти границы устанавливаются условно, полагая, что первый интервал по величине равен следующему за ним, а последний – предшествующему.
предварительно в каждом интервале определяется его середина, которая принимается за конкретное значение признака и умножается на соответствующую частоту. Середина интервала определяется как полусумма нижней и верхней границ интервала. Если у первого интервала нет нижней границы, а у последнего – верхней, то эти границы устанавливаются условно, полагая, что первый интервал по величине равен следующему за ним, а последний – предшествующему.

Важнейшее свойство средней арифметической: сумма отклонений вариантов от своей средней арифметической равна нулю
 .
.
Средняя гармоническая.
Средняя гармоническая простая  , где
, где  – обратные значения вариантов.
– обратные значения вариантов.
Средняя гармоническая взвешенная  , где M – веса.
, где M – веса.
Применение средней арифметической или средней гармонической определяется наличием данных и исходным статистическим соотношением (ИСС).
Кроме вышеуказанных средних, рассчитываются и структурные средние:
Мода (Мо) – это наиболее часто встречающееся значение признака у единиц совокупности. Для дискретных рядов – это вариант, имеющий наибольшую частоту (для наших данных Мо=20 тыс. руб.).
В интервальных вариационных рядах вначале по наибольшей частоте определяют интервал, в котором находится мода – модальный интервал. Для рядов с равными интервалами мода определяется по следующей формуле:
 ,
,
где  – нижняя граница модального интервала; i – величина модального интервала;
– нижняя граница модального интервала; i – величина модального интервала;  – частота (частость) предмодального интервала;
– частота (частость) предмодального интервала;  – частота модального интервала;
– частота модального интервала;  – частота послемодального интервала.
– частота послемодального интервала.
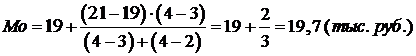 .
.
В ряду с неравными интервалами Мо определяется в интервале, имеющем наибольшую плотность распределения, и в формуле вместо частот принимаются соответствующие плотности распределения. Плотность распределения рассчитывается делением количества единиц в интервале на величину интервала.
Медиана (Ме) – это значение признака у средней единицы ранжированного ряда. Ранжированным называется ряд, у которого значения признака расположены в порядке возрастания или убывания.
Для нахождения медианы в случае несгруппированных данных вначале определяют её порядковый номер:  . Если n – нечётное число, то в центре ряда находится одно значение признака, и оно будет являться медианой; если же n – чётное число, то в центре ряда стоят два варианта, и медиану нужно определять как среднюю из величин этих вариантов.
. Если n – нечётное число, то в центре ряда находится одно значение признака, и оно будет являться медианой; если же n – чётное число, то в центре ряда стоят два варианта, и медиану нужно определять как среднюю из величин этих вариантов.
| 15 | 17 | 17 | 18 | 20 | 20 | 20 | 20 | 23 | 24 | 25 |
| №1 | №2 | №3 | №4 | №5 | №6 | №7 | №8 | №9 | №10 | №11 |

Для определения медианы в дискретном ряду также находят её порядковый номер:  . Далее рассчитывают накопленные частоты (частости) S путём последовательного суммирования частот всех вариантов, начиная с первого и заканчивая данным. Медианой является тот вариант, накопленная частота которого впервые больше или равна медианного номера:
. Далее рассчитывают накопленные частоты (частости) S путём последовательного суммирования частот всех вариантов, начиная с первого и заканчивая данным. Медианой является тот вариант, накопленная частота которого впервые больше или равна медианного номера:  .
.
| x | 15 | 17 | 18 | 20 | 23 | 24 | 25 | Итого |
| m | 1 | 2 | 1 | 4 | 1 | 1 | 1 | 11 |
| S | 1 | 1+2=3 | 1+2+1=4 | 1+2+1+4=8 | 1+2+1+4+1=9 | 1+2+1+4+1+1=10 | 1+2+1+4+1+1+1=11 | – |
 8>6 Ме=20 тыс. руб.
8>6 Ме=20 тыс. руб.
В интервальном ряду, прежде всего, находят медианный интервал; им считается тот, накопленная частота которого впервые больше или равна половины всей суммы частот  .
.
Медиана в этом случае находится по формуле:
 ,
,
где  – нижняя граница медианного интервала; d – величина медианного интервала;
– нижняя граница медианного интервала; d – величина медианного интервала;  – сумма частот (частостей) ряда;
– сумма частот (частостей) ряда; 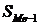 – накопленная частота до медианного интервала;
– накопленная частота до медианного интервала;  – частота медианного интервала.
– частота медианного интервала.


ТЕМА 2 «Показатели вариации»
1) Размах вариации R  .
.
Этот показатель используется нечасто, т.к. учитывает только крайние значения признака, которые могут существенно отличаться от всех других единиц. Применяется для определения величины интервала, когда известно число формируемых групп:
 , где k – число групп;
, где k – число групп;
2) Среднее линейное отклонение 
 – для несгруппированных данных;
– для несгруппированных данных;
 – для вариационного ряда.
– для вариационного ряда.
Чем меньше  , тем более однородна совокупность, тем более типична средняя для совокупности.
, тем более однородна совокупность, тем более типична средняя для совокупности.
Для интервального ряда предварительно определяют середины интервалов, т.е. переходят к дискретному ряду.
3) Среднее квадратическое отклонение (стандартное отклонение)  («сигма»)
(«сигма»)
 – для несгруппированных данных;
– для несгруппированных данных;
 – для вариационного ряда.
– для вариационного ряда.
4) Дисперсия 
 - для несгруппированных данных;
- для несгруппированных данных;
 - для вариационного ряда.
- для вариационного ряда.
Имеется и другая формула для исчисления дисперсии:

Дисперсия альтернативного признака: альтернативными признаками называются такие, которыми одни единицы изучаемой совокупности обладают, а другие – нет.
Пусть наличие признака обозначается 1, а его отсутствие – 0. Тогда через p обозначим долю единиц, обладающих признаком, а через q – долю единиц, этим признаком не обладающих:  . Получаем дискретный вариационный ряд:
. Получаем дискретный вариационный ряд:
| x | 1 | 0 | Итого: |
| w | p | q | 
|
Вначале определяем среднюю:  .
.
Дисперсия в этом случае равна:  .
.
5) Коэффициент вариации является относительным показателем вариации и представляет собой процентное отношение среднего квадратического отклонения к средней арифметической:
 .
.
Чем меньше значение v, тем однороднее совокупность, и тем точнее средняя отображает значения варьирующего признака. Совокупность считается однородной, если коэффициент вариации не превышает 33%.






