В долгосрочном периоде не только труд, но и капитал, производственные технологии является переменным фактором производства. Технический прогресс означает, что тот же объем выпуска можно получить с меньшими затратами труда и капитала. Геометрически все изокванты сдвигаются вниз к началу координат (рис. 1.18):

Рис. 1.18. Сдвиг изокванты вследствие технического прогресса
В долгосрочном периоде не действует закон убывающей производительности какого-либо производственного фактора, т.к. все факторы изменяются. Поэтому применительно к данному периоду говорят только об отдаче от масштаба.
Отдача от масштаба показывает, во сколько раз возрастает выпуск при увеличении всех факторов производства в n раз.
Аналитически отдачу от масштаба можно определить по производственной функции вида:
Q = AK a L b,
где
· Q – заданный объем выпуска;
· L – количество используемого труда;
· K – количество используемого капитала.
· А – заданный параметр отражающий влияние технического прогресса на производство. Если производитель внедряет передовые технологии, величина данного параметра возрастает, т.е. выпуск увеличивается при прежних количествах труда и капитала.
· a и b - это коэффициенты эластичности выпуска соответственно по капиталу и труду.
Отдача от масштаба бывает трех видов:
1) возрастающая отдача от масштаба - при увеличении всех факторов производства в n раз выпуск возрастает более чем в n раз;
2) убывающая отдача от масштаба - при увеличении всех факторов производства в n раз выпуск возрастает менее чем в n раз;
3) постоянная отдача от масштаба - при увеличении всех факторов производства в n раз выпуск возрастает тоже в n раз.
Коэффициент эластичности выпуска от масштаба рассчитывается по формуле:

Геометрически все три случая будут выглядеть так. При постоянной отдаче от масштаба расстояние между изоквантами остается прежним (рис. 1.19).

Рис. 1.19. Постоянная отдача от масштаба
При возрастающей отдаче от масштаба расстояние между изоквантами все время сокращается (рис. 1.20):

Рис. 1.20. Возрастающая отдача от масштаба.
При убывающей отдаче от масштаба расстояние между изоквантами увеличивается (рис. 1.21):

Рис. 1.21. Убывающая отдача от масштаба
На практике, когда предприятие начинает увеличивать труд и капитал, оно сначала сталкивается с возрастающей отдачей от масштаба. Например, при росте труда и капитала в два раза, выпуск увеличивается втрое, что говорит о сокращении затрат на единицу продукции и о повышении эффективности производства. Однако дальнейшее увеличение используемых ресурсов рано или поздно приводит к тому, что возрастающая отдача от масштаба сменяется постоянной, а затем и убывающей. Эффективность производства падает. Это служит сигналом к тому, что предприятие стало слишком крупным и его размер целесообразно уменьшить.
Теорема ДжонсонаВикселля:
В долгосрочном периоде (Q = AK a L b), эластичность выпуска от масштаба равна сумме эластичностей выпуска от используемых факторов производства:
ε Qm = ε QL + ε QK,
где
a = εQL
b = εQK.
Отсюда:
· при a + b =1 выпуск возрастает ровно в n раз, т.е. отдача от масштаба постоянна.
· при a + b >1 выпуск увеличивается более чем в n раз, т.е. отдача от масштаба возрастает.
· при a + b <1 выпуск увеличивается менее чем в n раз, т.е. имеет место убывающая отдача от масштаба.
Равновесие производителя.
Изокоста – это линия, точки на которой отражают всевозможные варианты каждой пары ресурсов K и L, которые может приобрести производитель при данных их ценах и номинальном доходе.

Рис. 1.22. Изокоста.
Уравнение изокосты:
Р L × QL + Р K × QK = ТС,
где
o Р L и Р K – цены факторов производства;
o QL и QK – количество факторов производства;
o ТС – расходы (доход) производителя (величина постоянная).
Угол наклона изокосты к оси L определяется обратным соотношением цен на ресурсы.
Проанализируем экономическую ситуацию. Пусть нам дана производственная функция Q = 7 K 2/9 L7/9. Цены на ресурсысоответственно составляют 4 и 3 условные единицы (у.е). Величина расходов производителя постоянная и равна 24 у. е.
Определим:
1. период производства;
2. количество ресурса, которое приобретет рациональный производитель при данных ценах и денежном доходе, исходя из сложившейся производственной задачи.
Рассуждения:
Анализируемый период производства долгосрочный, т.к. заданная производственная функция степенная.
Для того, чтобы определить количество ресурса, которое приобретет рациональный производитель воспользуемся правилами минимизации затрат или максимизации прибыли (рис. 1.23):
o производитель минимизирует затраты при условии, когда каждый последний рубль, затраченный им на ресурсы даёт одинаковый предельный продукт (правило минимизации затрат).
o предельные продукты всех факторов производства в стоимостном выражении равны их ценам, или каждый ресурс используется до тех пор, пока его предельный продукт в денежном выражении не станет равен цене (правило максимизации прибыли):


Рис. 1.23. Предельная производительность, цена и степень использования ресурса в производстве.
Первая производная производственной функции Q = 7 K 2/9 L7/9 даст нам следующие предельные величины:
MPL = (Q)′ L = 49/9(K / L)2/9
MPK = (Q)′ K = 14/9 (L/ K)7/9
Если мы соответствующие предельные величины соотнесем с их ценами, то получим тождество:
22(K / L)2/9 = 5(L / K)7/9
Согласно данным правилам производитель должен израсходовать весь свой денежный ресурс, поэтому составим следующую систему уравнений и решим ее:

Мы получим, что рациональный производитель приобретет количество единиц труда L = 6,3, капитала K = 1,3.
Геометрически равновесие производителя можно отобразить следующим образом (рис. 1.24):

Рис. 1.24. Равновесие производителя.
2.2.5. Анализ затрат производства в краткосрочном периоде
В краткосрочном периоде общие или валовые издержки (TC) состоят из постоянных (FC) и переменных (VC).
TC( Q ) = FC + VC,
где
o FC – постоянные издержки, величина которых не зависит от объёма производства. К ним относятся: заработная плата повременных работников; банковский процент за кредит; плата за коммунальные услуги; арендные платежи; амортизационные отчисления.
o VC – переменные издержки, величина которых растёт по мере увеличения объёма производства. К ним относят расходы на: сырьё, материалы, топливо, заработную плату сдельщиков.
Допустим, что функция общих издержек фирмы на выпуск Q единиц продукции представлена следующим образом:
TC = Q² + 16Q + 400.
Выведем уравнения функций всех видов издержек, используемых в экономической теории для описания поведения фирмы.
Отсюда, согласно теории:
o FC = 400 – это постоянные издержки, т.к. они не зависят от выпуска продукции (Q);
o VC = Q² + 16Q – переменные издержки – зависят от выпуска продукции (Q).
Для экономического анализа деятельности фирм, предприятий особый интерес представляют средние и предельные издержки.
Средние общие издержки (AC или ATC) – это общие расходы на единицу выпуска продукции:
AТC = TC / Q = (FC / Q + VC / Q),
где
o FC / Q = AFC - средние постоянные издержки;
o VC / Q = AVC – средние переменные издержки.
Средние переменные издержки (AVC) – это переменные издержки на единицу выпуска продукции:
AVC = VC / Q = Q + 16.
Средние постоянные издержки (AFC) – это постоянные издержки на единицу выпуска продукции:
AFC = FC / Q = 400 / Q.
Применительно к анализируемой нами функции общих издержек, уравнение функции средних общих издержек примет вид:
AТC = (Q + 16) + 400 / Q.
Предельные (маржинальные) издержки (MC) – это прирост издержек на выпуск дополнительной единицы продукции:
MC = ∆TC / ∆Q
или MC = dTC / dQ, т.е. производная общих издержек.
Тогда уравнение функции предельных издержек, анализируемой нами функции общих издержек, будет иметь следующий вид:
MC = 2Q + 16.
Таким образом функция затрат производства отражает зависимость между объемом произведенной продукции и минимально необходимыми затратами на его производство.
Характер изменения краткосрочных издержек производства можно изобразить графически:

Рис. 1.25. Издержки производства в краткосрочном периоде.
Проведем анализ данного графического изображения, опираясь на общеизвестные теоретические положения:
1 участок: от 0 до Q1 характеризует снижение всех видов издержек (предельных и средних);
2 участок: от Q1 до Q2 – снижение средних переменных, постоянных и общих средних издержек при повышении предельных.
3 участок: от Q2 до Q3 отражает повышение предельных и средних переменных издержек при соответствующем снижении
средних общих издержек. При объёме выпуска продукции Q3 достигается минимум средних общих издержек, т.е. производственный оптимум (AТC = MC).
Производственный оптимум предполагает достижение такого объёма выпуска, при котором все производственные мощности, задействованы полностью, работники работают без прогулов и перенапряжения. Применительно к анализируемой нами функции общих издержек фирмы: TC = Q² + 16Q + 400 можно заключить, что оптимальный выпуск продукции достигнут при объеме выпуска продукции Q3 = 20 (AТC = MC или Q + 16 + 400 / Q = 2Q + 16). Следовательно, точка Q3 = 20 – точка производственного оптимума.
4 участок: от Q3 и выше – одновременное повышение всех видов издержек. Значит, дальнейшее увеличение выпуска продукции будет невыгодным.
На величину издержек производства в краткосрочном периоде влияют следующие факторы:
o общий выпуск продукции;
o закон убывающей предельной производительности;
o эффект масштаба.
Скорость увеличения издержек зависит от производительности труда. Теоретически между средними переменными издержками и средней производительностью труда (средним продуктом) существует прямая связь, т.к. средний продукт равен объему выпуска на единицу используемого фактора. Но так как в нашей ситуации ставка заработной платы фиксирована, то между средними переменными издержками (предельными издержками) и средним продуктом (предельным продуктом) соответственно существует обратная зависимость.
Эффект масштабапроизводства – реакция объёма выпуска на изменение масштаба производства.Масштаб производства определяется размером используемых ресурсов (см. рис. 1.26).

Рис. 1.26. Реакция объёма выпуска продукции на изменение масштаба производства.
1 участок – если с ростом выпуска продукции средние издержки снижаются, то говорят, что наблюдается положительный эффект масштаба (растущая отдача);
2 участок – если издержки не зависят от масштаба производства, то это нулевой эффект (постоянная отдача);
3 участок – если с ростом выпуска растут средние издержки, то это отрицательный эффект (убывающая отдача).
Определим эффект масштаба производства на основе анализа функции общих издержек производства: TC = Q² + 16Q + 400.
Вычислим значение выпуска Q, при котором средние общие издержки минимальны. Для этого необходимо найти первую производную общих средних издержек и приравнять её к нулю:
(ATC)' = (Q + 16 + 400 / Q)' = 1 – 400 / Q² = 0.
Отсюда получим, что при Q = 20 средние общие издержки будут минимальны. Значит, до объёма выпуска Q = 20 наблюдается положительный эффект масштаба производства, а начиная с Q = 20, имеет место отрицательный эффект масштаба.
Следовательно, если:
o (ATC)' < 0 – положительный эффект масштаба производства;
o (ATC)' > 0 – отрицательный эффект масштаба производства;
o (ATC)' = 0 – постоянный эффект масштаба производства.
2.2.6. Затраты производства в долгосрочном периоде
Функционирование фирм в долгосрочном периоде теоретически предполагает ряд допущений:
o все факторы производства и труд, и капитал и НТП, являются переменными;
o цены на факторы производства неизменны;
o средние постоянные издержки исчезают в силу большого объема выпуска продукции, а значит А FC = 0;
o средние переменные издержки равны средним общим AVC = A Т C (в долговременном периоде используется только понятие кратковременные средние издержки – SRAC);
o между предприятиями, к примеру П1–4, входящими в состав фирмы, возможен перелив капитала;
o А, В, С, D – точки минимума краткосрочных средних издержек, т.е. точки оптимального выпуска продукции;
o LRAC – долгосрочные средние издержки;
o принцип минимизации издержек определяется по предельному продукту труда в расчете на единицу стоимости данного фактора;
o на участке [OD] прослеживается растущая отдача или положительный эффект масштаба производства;
o выше этого участка идет повышение долговременных средних издержек.
Графическое изображение долгосрочных средних издержек (см. рис. 1.27).

Рис. 1.27. Долгосрочные средние издержки.
2.2.7. Производство в условиях совершенной конкуренции и монополии
Конкуренция – это экономическая борьба, соперничество за рынок сбыта, за сферу вложения капитала.
Методы конкуренции бывают: ценовые и неценовые.
Рыночная власть – это способность продавца или покупателя влиять на цену продукции и объём продаж.
Коэффициент Лернера (L), отражающий рыночную власть:
(P – MC) / P = |1 / Ed|
Рассмотрим рынок совершенной конкуренции на конкретном примере. Цена единицы продукции задана и равна 4 д.е. Данные об объёме выпуска продукции фирмы и издержках производства приведены в таблице:
| Количество единиц продукции Q, шт. | Общие издержки TC | Постоянные издержки FC | Переменные издержки VC |
| 0 | 150 | 0 | |
| 5 | 20 | ||
| 15 | 40 | ||
| 30 | 60 | ||
| 50 | 80 | ||
| 75 | 100 | ||
| 95 | 120 | ||
| 110 | 140 | ||
| 120 | 160 | ||
| 125 | 180 | ||
| 125 | 200 |
1. Рассчитаем значения всех видов издержек производства фирмы, используемых в экономической теории для описания ее поведения.
2. Начертим график, отражающий поведение фирмы на рынке совершенной конкуренции.
3. На основе расчетов и графика, обоснуем:
а) характерные черты фирмы на рынке совершенной конкуренции,
б) стратегию фирмы на данном рынке.
Решение:
1. Расчетные значения всех видов издержек, используемых в экономической теории для описания поведения фирмы, сведем в следующую таблицу:
| Q | TR | FC | VC | TC | AFC | AVC | ATC | AR | MC | MR | PR |
| 0 | - | 150 | 0 | 150 | - | - | - | - | - | - | - 150 |
| 5 | 20 | 20 | 170 | 30 | 4 | 34 | 4 | 4 | 4 | - 150 | |
| 15 | 60 | 40 | 190 | 10 | 2,66 | 12,6 | 4 | 2 | 4 | - 130 | |
| 30 | 120 | 60 | 210 | 5 | 2,0 | 7,0 | 4 | 1,33 | 4 | - 90 | |
| 50 | 200 | 80 | 230 | 3 | 1,6 | 4,6 | 4 | 1 | 4 | - 30 | |
| 75 | 300 | 100 | 250 | 2 | 1,33 | 3,33 | 4 | 0,8 | 4 | 50 | |
| 95 | 380 | 120 | 270 | 1,58 | 1,26 | 2,84 | 4 | 1 | 4 | 110 | |
| 110 | 440 | 140 | 290 | 1,36 | 1,27 | 2,64 | 4 | 1,33 | 4 | 150 | |
| 120 | 480 | 160 | 310 | 1,25 | 1,33 | 2,58 | 4 | 2 | 4 | 170 | |
| 125 | 500 | 180 | 330 | 1,20 | 1,44 | 2,64 | 4 | 4 | 4 | 170 | |
| 125 | 500 | 200 | 350 | 1,20 | 1,6 | 2,8 | 4 | - | - | 150 |
2. На основе данных расчетов начертим график, отражающий поведение фирмы на рынке совершенной конкуренции (рис.1.28).

Рис. 1.28. Фирма на рынке совершенной конкуренции.
3. а) Характерные черты фирмы на рынке совершенной конкуренции.
o Период производства кратковременный, поскольку именно он характеризуется невозможностью изменения постоянных издержек (величина FC = 150 д.е. неизменна при любом объме выпуска продукции).
o Фирма – ценополучатель ( цена единицы продукции задана и равна 4 д.е.)
o Коэффициент Лернера ((P – MC) / P = |1 / Ed|) равен нулю, данная рыночная структура не имеет рыночной власти.
Предельный и средний доходы при любом объеме производства величины постоянные и равны цене:
P = 4 = MR = AR.
Согласно закону спроса: чем выше цена, тем ниже спрос или наоборот. Однако спрос на данном рынке является совершенно (абсолютно) эластичным. D = MR = AR. Поэтому линия спроса на продукцию фирмы данного рыночного пространства горизонтальна и совпадает с линией предельного и среднего дохода.
б) Стратегия фирмы на рынке совершенной конкуренции.
Для определения объёма производства, максимизирующего прибыль, воспользуемся правилом максимизации прибыли:
MC = MR = Р
Правило максимизации прибыли выдерживается при объёме выпуска продукции: Q = 5 и Q = 125 единиц. При Q = 5 фирма несёт убытки равные 150 д.е., а при Q = 125 ед. прибыль фирмы максимальная (PR = 170 д.е.). Следовательно, оптимальным объёмом производства будет Q = 125 единиц. При данном выпуске продукции MC = P = 4 = MR = AR.
Условие максимума прибыли для фирмы рынка совершенной конкуренции будет выглядеть следующим образом:
MC = P = MR = AR.
Несмотря на то, что в интервале от Q= 5 ед. продукции до Q = 75 ед фирма несёт убытки, ей не стоит уходить с рынка. В случае ухода с рынка убытки фирмы будут равны расходам, связанным с приобретением постоянных факторов производства (FC = 150 д.е.) Если фирма останется в отрасли, то убытки будут меньше на величину постоянных издержек: (FC + VC – PQ) < FC(при этом AVC < P, а VC < PQ). Отсюда стратегия конкурентной фирмы в кратковременном периоде должна состоять в следующем:
o фирма продолжает производство, если min AVC ≤ P < min ATC. В экономической теории такая ситуация называется минимизирующей убытки фирмы.
o AVC ≥ P, то фирме стоит уйти с рынка, т.к. каждая выпускаемая единица продукции приносит дополнительные убытки.
o При увеличении производства продукции с 75 единиц фирма получает экономическую прибыль т.к. AТC < P.
Общетеоретические выводы:
o Линия предложения в кратковременном периоде совпадает с линией предельных издержек на отрезке: min AVC ≤ P < min ATC.
o Линия предложения в долговременном периоде совпадает с линией предельных издержек, начиная с выпуска продукции, при котором цена P ≥ minA Т C.Экономическая прибыль фирмы в долговременном периодеравна нулю, если выдерживается условие:
MR = AR = MC = AC = P
Причиной этого является тот факт, что в данном периоде возможен перелив капитала из менее прибыльных отраслей в более прибыльные. Перелив капитала способствует увеличению предложения продукции отрасли и соответственно снижению равновесной цены при неизменном рыночном спросе. Тогда новая цена будет равна величине средних общих и предельных издержек традиционной фирмы: P = AC = MC.
Чистая монополия – единственный производитель уникального продукта (рис. 1.29).

Рис. 1.29. Чистая монополия.
Характерные черты чистой монополии:
o Монополист обладает рыночной властью. Коэффициент Лернера ((P – MC) / P = |1 / Ed|) больше нуля.
o Производство продукции фирмы – монополиста ограничено рыночным спросом (D = AR).
o Цена на продукцию фирмы – монополиста выше, чем половина запретительной цены (А/2).
o Объем производства продукции ниже, чем половина массы насыщения (В/2).
o Правило максимизации прибыли предполагает равенство MCиMR. Монопольная прибыль определяется разницей между TR и TC.
Рассмотрим поведение фирмы – монополиста на следующем примере. Даны функция издержек производства фирмы – монополиста TC = ¼ Q² + 10Q + 300; и функции спроса на продукцию этой монополии на двух рынках: Q(1) = 400 – 2P(1);Q(2) = 600 – 4P(2).
А) Найдём объёмы продаж и цены на каждом из двух рынков, максимизирующие прибыль, при условии, что ценовая дискриминация незапрещена государством?
Б) Определим прибыль монополиста при ценовой дискриминации.
В) Как изменятся объём продаж, цены и прибыль, если ценовая дискриминация запрещена государством?
Рассуждения:
Мы знаем, что монополист, может производить любой объем продукции и продавать ее по цене, какой захочет. Главная цель монополиста – получить максимум прибыли при имеющихся возможностях.
Ценовая дискриминация – это продажа товара разным покупателям по разным ценам. Согласно закону спросу: чем выше цена, тем меньше реализуемый объем производства, или наоборот. Между тем от монополиста не зависит существующий на рынке спрос и уровень его издержек в данный момент времени.
Попробуем найти тот объем производства и соответственно уровень цен на каждом из двух рынков, максимизирующие прибыль монополиста при условии, что ценовая дискриминация незапрещена государством.
Решение:
А) Воспользуемся правило м максимизации прибыли монополиста при ценовой дискриминации:
MC = MR(1) =MR(2),
где 1, 2 – число разных групп покупателей, приобретающих монопольный товар по разным ценам.
Данное правило основано на принципе выравнивания предельных доходов, получаемых на каждом из двух рынков.Поскольку достигнутый при этом уровень доходов может быть выше или ниже предельных издержек, то для получения наибольшей массы прибыли необходимо или сокращать объём выпуска, или наращивать.
Первая производная общих издержек есть предельные издержки:
(TC)’ = MC = ½Q + 10.
Поскольку монополист функционирует на двух рынках, то функция предельных издержек примет следующий вид:
MC = ½ (Q(1) + Q(2)) + 10.
Выведем функции предельного дохода (MR(1) и MR(2)) монополиста на двух рынках. Функция предельного дохода есть первая производная общего дохода: MR = (TR)’ = (P × Q)’.
Поскольку спрос на первом рынке составляет Q(1) = 400 – 2P(1),а спрос на втором рынке равен Q(2) = 600 – 4P(2),то обратные функции спроса, отражающие зависимость цены спроса от величины спроса соответственно примут соответствующий вид: P(1) = 200 – ½ Q(1) иP(2) = 150 – ¼ Q(2).
Отсюда функции предельного дохода на двух рынках составят:
· MR(1) =(TR)’ =((200 – ½ Q) × Q)’ = (200Q – ½ Q²)’ = 200 – Q(1);
· MR(2 ) =(TR)’ =((150 – ¼ Q) × Q)’ = (150Q – ¼ Q²)’ = 150 – ½Q(2).
Составим и решим систему уравнений:

Решим выражение(2) и подставим в первое (1). Получим:
Q(2) = 2 Q(1) – 100.
Подставляем Q(2) в первое выражение и находим Q(1):
½ (Q(1) + 2Q(1) – 100) + 10 = 200 – Q(1).
Следовательно, объем производства на каждом из двух рынков, максимизирующие прибыль монополиста составят:
o Q(1) = 96 штук;
o Q(2) = 92 штук.
Вычислим уровень цен на каждом из двух рынков, максимизирующий прибыль монополиста:
o P(1) = 200 – ½ × 96 = 152 д.е.
o P(2) = 150 – ¼ × 92 = 127 д.е.
Б) Подсчитаем прибыль монополиста при ценовой дискриминации по формуле: PR = TR – TC.
o TR = (Q(1) × P(1) + Q(2) × P(2)) =(96 × 152 + 92 × 127) = 26 276 д.е.
o TC = ¼ (Q(1) + Q(2))² + 10(Q(1) + Q(2)) + 300 = (¼ × 188² + 10 × 188 + 300) = 11 016 д.е.
o PR = 15 260 д.е.
В) Как изменятся объём продаж, цены и прибыль, если ценовая дискриминация запрещена государством?
Во всех экономически развитых странах существует антимонопольное законодательство. Данные законы объявляют незаконными действия лиц, которые осуществляют дискриминацию в ценах между различными покупателями товаров одного и того же сорта, качества, когда результатами такой дискриминации является существенное ограничение конкуренции. Данный закон не налагает уголовной ответственности (т.е. является актом гражданского кодекса).
Если ценовая дискриминация будет запрещена государством, то товар на обоих рынках будет продаваться по одной и той же цене. Отсюда общий рыночный спрос составит:
Q(D) = (400 – 2P(1)) + (600 – 4P(2))= 1 000 – 6P.
Тогда обратная функция спроса примет следующий вид:
P = 167 – 1/6Q.
Определим объём производства, максимизирующий прибыль. Найдём Q, исходя из условия максимизации прибыли MC = MR.
· MC = ½Q + 10; а
· MR = (TR)’ = ((167 - 1/6 Q) × Q)’ = (167 Q – 1/6 Q²)’ = 167 – 1/3 Q.
Приравняем значения MC и MR:
0,5Q + 10 = 167 – 1/3Q.
Следовательно, Q ≈ 188 шт., а Р ≈ 167 – 1/6 × 188 ≈ 136 д.е.
Найдем максимальное значение прибыли: PR = TR – TC.
PR = 188 × 136 – (¼ × 188² + 10 × 188 + 300) = 14 552 д.е.
Прирост прибыли монополиста при ценовой дискриминации составил: 708 ден.ед. (15260 – 14552).
2.2.8. М одели антимонопольного регулирования.
Основу американской модели представляют три нормативно-правовых акта США:
1. Закон Шермана("Закон, направленный на защиту торговли и промышленности от незаконных ограничений и монополий" 1890г.) признает незаконным всякий договор, либо сговор, направленный на ограничение развития промышленности или свободы торговли. Лицо, признанное виновным в соответствующем нарушении подвергается штрафу или тюремному заключению.
2. Закон "О Федеральной торговой комиссии" (1914г.) позволяет фирмам, ведущим хозяйственную деятельность на рынках США, приобретать не менее 15% голосующих акций предприятий США при соблюдении следующих ограничительных условий:
o обязательна межштатная торговля;
o один из участников сделки должен иметь активы или объемы продаж на $ 100 млн. или более, а второй участник не менее чем $ 10 млн.;
o предметом сделки должен быть пакет акции с правом голоса в размере не менее 15%, либо цена сделки должна быть не менее 15 млн. долларов;
o Федеральная торговая комиссия США должна быть уведомлена о совершении сделок по пакетам акций с правом голоса от 5% до 15%.
1. Закон Клейтона объявляет незаконными действия лица, которое осуществляет дискриминацию в ценах между различными покупателями товаров одного и того же сорта, качества, когда результатами такой дискриминации явится существенное ограничение конкуренции или же тенденция к образованию монополий в любой сфере деятельности. Данный закон является актом гражданского кодекса.
Вывод:
o американская модель построена на принципе запрещения монополии как структурной единицы независимо от социально-экономических последствий ее деятельности;
o европейская модель построена на принципе регулирования монополистической практики путем устранения его отрицательных социально-экономических последствий.
Российская антимонопольная практика больше всего тяготеет к европейской модели. Основу антимонопольного законодательства России составляют: Конституция РФ, Закон РСФСР "О конкуренции и ограничении монополистической деятельности на товарных рынках" 1991г. (значительно переработан в 1995г.), а также изданные в соответствии с ними федеральные законы, указы Президента, постановления и распоряжения правительства.
Специфика антимонопольной политики России состоит в том, чтобы:
o использовать выгоды крупномасштабной экономики;
o нейтрализовать возможные негативные последствия, связанные с ослаблением конкуренции.
o сохранить некоторые виды монополий, обеспечивая их государственное регулирование (в частности, денежно-эмиссионную деятельность; экспорт, импорт отдельных товаров; производство и сбыт алкогольной продукции и др.)
o контролировать деятельность естественных монополий, используя следующие методы:
1. ценовое регулирование, осуществляемое посредством определения цен (тарифов) или их предельного уровня;
2. определение потребителей, подлежащих обязательному обслуживанию;
3. установление минимального уровня обеспечения потребности товаром, в случае, если невозможно удовлетворить данную потребность в полном объеме.
2.3. ДЛЯ КОГО ПРОИЗВОДИТЬ ИЛИ ТЕОРИЯ ПОТРЕБИТЕЛЬСКОГО ВЫБОРА
2.3.1. Потребительский выбор: понятие, свойства
Потребительский выбор – выбор, максимизирующий функцию полезности рационального потребителя в условиях ограниченности ресурсов.
Полезность – субъективное восприятие продукта или услуги потребителем, т.е. их ценность для него
Функция полезности:
U = f (Qx; Qy; Qz...),
где
o U – уровень полезности;
o Qx; Qy; Qz - количество потребляемых продуктов или услуг за определённый период времени;
o f – зависимость уровня полезности от количества потребляемых продуктов и услуг.
Различают функции:
o общей полезности (TU);
o предельной полезности (MU).
Общая полезность – сумма добавочных полезностей определенного продукта, который потребляет индивид:
TUn = MU 1 + MU 2 + … + MUn.
Поведение функции общей полезности изучим на основе ее графического изображения (рис. 1.30.).

Рис. 1.30. Графическое изображение функции общей полезности:
o Q – количество (например, обувь);
o U – полезность.
Как видно из графика, функция общей полезности возрастает, а затем, достигнув своего максимального значения, убывает:
TUmax = 4 + 2 + 1,5 + 0,5 + 0,2 = 8,2;
где
o ТU1 = 4;
o ТU2 = 4 + 2 = 6;
o ТU3 = 6 + 1,5 = 7,5;
o ТU4 = 7,5 + 0,5 = 8;
o ТU5 = 8 + 0,2 = 8,2;
o ТU6 = 8,2 – 0,2 = 8.
Так, две пары обуви обладают для потребителя большей полезностью, чем одна; три большей, чем две и т.д. Общая полезность растёт, хотя и медленными темпами, т.е. каждая дополнительная пара приносит все меньшую и меньшую полезность. При этом полезность шестой пары обуви отрицательна (MU6 = - 0,2), а значит, она уже приносит «вред». Отсюда можно сделать общий вывод: по мере увеличения количества потребляемого продукта (в частности обуви), общая полезность возрастает, а прирост полезности от каждой её порции (пары) убывает (суть закона возрастающей общей полезности). Тем самым потребность в них насыщается. Следовательно, полезность зависит:
o от количества потребляемого продукта (пар обуви);
o от интенсивности потребления.
Предельная полезность (MU) – добавочная полезность каждой последующей единицы продукта.
Предельная полезность определяется по формуле:
MU = ∆TU / ∆Q,
где
o ∆TU = TUn - TUn – 1;
o ∆Q = Qn– Qn – 1.
Опираясь на вышеизложенную теорию общей полезности и поведение потребителя обуви, построим график функции предельной полезности. По оси абсцисс отложим количество пар обуви, а по оси ординат значения добавочных (предельных) полезностей от потребления каждой последующей пары. Так, если:
o MU1 = TU1 – TU0 = 4;
o MU2 = TU2 – TU1 = 6 – 4 = 2;
o MU3 = TU3 – TU2 = 7,5 – 6 = 1,5;
o MU4 = TU4 – TU3 = 8 – 7,5 = 0,5;
o MU5 = TU5 – TU4 = 8,2 – 8 = 0,2;
o MU6 = TU6 – TU5 = 8 – 8,2 = - 0,2,
то график данной функциональной зависимости будет выглядеть следующим образом (см. рис. 1.31.):

Рис. 1.31. Графическое изображение функции предельной полезности.
На основе данного графика можно заключить, что график функции предельной полезности не выпукл, а даже вогнут. По мере увеличения количества потребляемых пар обуви добавочная полезность каждой последующей пары убывает (суть закона убывающей предельной полезности (первый закон Госсена)). Минимум предельной полезности достигается в точке, когда общая полезность достигла своего максимума (ТU5 = 8,2). Дальнейшее потребление обуви принесет «вред». Об этом свидетельствует предельная полезность шестой пары обуви:
MU 6 = (TU 6 – TU 5) / (Q 6 – Q 5) = 8 – 8,2 / 6 – 5 = - 0,2 / 1 = - 0,2.
Потребитель предъявляет спрос на тот или иной товар, исходя из его полезности.
Основные постулаты теории поведения потребителя:
o множественность видов потребления – желание потребителем потреблять множество разнообразных товаров;
o ненасыщенность – потребитель не пресыщен не одним из товаров или услуг;
o транзитивность – определенная согласованность вкусов потребителя;
o субституция – замена менее предпочтительного товара более предпочтительным товаром;
o убывающая предельная полезность.
2.3.2. Количественная теорияпотребительского поведения.
Основоположники количественной теории(Менгер, Визер, Госсен) считали, что полезность конкретных продуктов можно измерить. Единица измерения полезности – ютиль (англ. «utility – полезность)». В частных случаях для измерения полезности используют денежные единицы измерения, дополнительные баллы, бонусы и т.д.
Суть количественной теории: рациональный потребитель максимизирует общую полезность в том случае, когда денежный доход потребителя распределяется таким образом, что каждый последний рубль (доллар, евро и т.д.), затрачиваемый на приобретение продуктов или услуг, приносит одинаковую полезность (второй закон Госсена или правило максимизации полезности):
MU1 / P1 = MU2 / P2 = … MUn / Pn = λ,
где
o MU1; MU2; … MUn – предельные полезности потребляемых продуктов;
o P1; P2;… Pn – цены на данные продукты.
o λ – предельная полезность денег
Правило максимизации полезности отражает ситуацию потребительского равновесия. Тогда
MU = P ∙ λ,
где
o P ∙ λ – предельные издержки потребителя;
Следовательно, если MC = P ∙ λ, то MU = MC
где
MC – предельные издержки.
2.3.3. Порядковая теория полезности.
Основоположники порядковой теории, в частности, Слуцкий, Хикс, Парето исходили из того, полезность отдельных продуктов измерить нельзя, но можно расставить приоритеты, т.е. построить шкалу предпочтений.

Рис. 1.32. Кривая безразличия.
Кривая безразличия (U) показывает, что в каждой её точке есть набор, состоящий из двух продуктов, который обеспечивает одинаковое удовлетворение потребностей потребителя, т.е. данные наборы продуктов одинаково безразличны потребителю.
На основе этого рисунка мы можем сделать следующие выводы:
а) наборы продуктов, соответствующие точкам A, B, C, D, E, F имеют одинаковую полезность для потребителя (т.е. потребитель безразличен к шести наборам продуктов);
б) набор продуктов, соответствующий точке G, менее предпочтителен для потребителя;
в) набор из двух продуктов, соответствующий точке Н, более предпочтителен для потребителя.
Если через точки G и H провести кривые, параллельные исходной кривой, то получим карту кривых безразличия.
Карта кривых безразличия – это вкусы и предпочтения потребителей.
Свойства кривых безразличия на карте кривых безразличия:
o кривые безразличия не пересекаются, т.к. один набор продуктов, который предпочтительнее другого набора, не может находиться с ним на одном уровне;
o кривые безразличия имеют отрицательный наклон, т.к. увеличение количества одного продукта сопровождается уменьшением количества другого, входящего в тот же набор продуктов;
o кривые безразличия пологие, т.е. вогнуты. Чем менее полога кривая безразличия, тем ниже предельная норма замещения.
Нормой замещения (MRS) одного продукта другим называется такое количество продукта А, которым потребитель согласен пожертвовать, с тем чтобы приобрести дополнительную единицу продукта B, при их одинаковой общей полезности:
MRSAB = |- A / + B| = |MU В | / |MU А |
Различают:
o дуговую норму замещения;
o предельную норму замещения.
Дуговая норма замещения на отрезке АВ кривой безразличия:
MRSух= - ∆Y / ∆X.
Предельная норма замещения есть производная в любой точке кривой безразличия: 
MRS ху = ǀ - dY / dX ǀ = MUx / MUy
Формы кривых безразличия:
1.Взаимозависимые (заменяемые) блага – продукты или услуги, которые удовлетворяют потребности за счёт друг друга (например: чай и кофе, розы и гвоздики и т.д.) (Рис. 1. 33.)
2. Взаимодополняемые блага – продукты или услуги, которые удовлетворяют потребности лишь в комплексе друг с другом (например: доски и гвозди, фотоаппарат и пленка и т.д.) (Рис. 1.34.)
3. Независимые блага – продукты или услуги, которые удовлетворяют потребности независимо друг от друга (например: чай и гвозди). (Рис. 1.35.)
4. Нежелательные блага – продукты или услуги, без которых потребитель был бы рад обойтись, но в силу каких-то причин вынужден потребить (например: горькое лекарство, услуги стоматолога и т.д.) (Рис.1.36.)

Рис. 1.33. Рис. 1.34. Рис. 1.35. Рис. 1.36.
2.3.4. Бюджетное ограничение потребителя
Анализ потребительских предпочтений не показывает, какой из наборов продуктов купит покупатель. Следовательно, чтобы разобраться в этом, надо изучить покупательную способность потребителя. Для этого необходимо учитывать цены на продукты и доход потребителя.
Пусть X и Y - количество продукта, которое хотят приобрести покупатели.
o Pxи Py - цены на соответствующие продукты;
o I – номинальный доход потребителя (величина постоянная).
Тогда алгебраически бюджетное ограничение потребителя примет следующий вид:
Px × X + Py × Y = I.
На основе данного тождества построим бюджетную плоскость:

Рис. 1.37. Бюджетная плоскость.
На основе данного рисунка сделаем следующие выводы:
o заштрихованная плоскость есть бюджетное пространство (бюджетные возможности покупателя);
o все точки, лежащие внутри бюджетного пространства, показывают доступность потребителю данных продуктов (однако, приобретая их, он не полностью использует свой доход);
o наборы продуктов, лежащие за бюджетной линией предпочтительны для потребителя, но не доступны, т.к. его доход не позволяет ему их приобрести.
Бюджетная линия – линия, которая графически отражает набор продуктов, приобретение которых требует одинаковых затрат.
Уравнение бюджетной линии:

Поведение бюджетной линии, исходя из следующих ситуаций:
o если цены на продукты Х и Y постоянны, а номинальный доход растет, то бюджетная линия переместится вверх параллельно первоначальной линии;
o если номинальный доход постоянен, а цены на продукты Х и Y упали, то бюджетная линия переместится вверх параллельно первоначальной, т.к. реальный доход вырос;
o если номинальный доход и цена на продукт Y постоянны, а цена на продукт Х падает, то спрос на продукт Y не изменится, а на продукт Х возрастёт.
2.3.5.Условие равновесия потребителя.
Дано:
1. Три кривых безразличия U1–U3.
2. Бюджетное ограничение Рх × Х + Py × Y = I,
где
I – номинальный доход (величина постоянная).
3. Наборы продуктов, соответствующие точкам A, B, C, D, E и F.
Доказать: что набор продуктов, соответствующий точке C (рис. 1.38.), отражает ситуацию потребительского равновесия, в которой рациональный потребитель достигает максимум общей полезности.

Рис. 1.38. Положение равновесия потребителя.
Доказательство:
Количественная теорияповедение кривых безразличия U1–U3объясняет с точки зрения убывающей предельной полезности (первый закон Госсена).
Порядковая теория поведение кривых безразличия U1–U3 объясняет с точки зрения снижающейся предельной нормы замещения (MRS). В любой точке кривой безразличия предельная норма замещения будет выражать следующую зависимость:
MRSxy = ǀ - dY ǀ / ǀ dX ǀ = MUx / MUy.
Рассмотрим положение бюджетной линии и кривых безразличия U1 – U3 в бюджетной плоскости:
1. для потребителя более предпочтительны наборы из двух продуктов (X,Y), соответствующие точкам E и F (кривая безразличия U3). Однако, они ему не доступны, т.к. не хватает дохода;
2. если потребитель предпочтет наборы из двух продуктов(X,Y) кривой безразличия U1 (точка A, B и D), то он поступит нерационально. При данном уровне потребления доход используется им не полностью (заштрихованная часть бюджетного пространства);
3. рациональный потребитель увеличит степень удовлетворения своих потребностей (при том же бюджетном ограничении), перейдя с кривой безразличия U1 на U2 (точка C).
Проанализируем положение точки C:
Точка C – точка касания кривой безразличия U2 и бюджетной линии. В данной точке тангенс угла наклона кривой безразличия равен тангенсу угла наклона бюджетной линии.
Тангес угла наклона есть производная функции или отношение противолежащего катета к прилежащему катету.
Возьмём производную в точке C:
 .
.
Поскольку в теории потребления номинальный доход потребителя величина постоянная, то количество сэкономленных денег от недопотребления товара Y, должно соответствовать количеству денег, потраченных на приобретение товара X. Отсюда, приравняв производные:
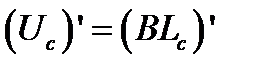 ,
,
получим следующее выражение:
 .
.
Таким образом, набор из двух продуктов, соответствующий точке C отражает ситуацию потребительского равновесия, в которой рациональный потребитель достигает максимум общей полезности (второй закон Госсена). Это и требовалось доказать.
2.3.6. Эффект дохода и эффект замещения.
Эффект дохода показывает изменение величины спроса, обусловленное исключительно изменением реального дохода при прежних относительных ценах.
Эффект замены показывает изменение величины спроса обусловленное исключительно изменением относительной цены товара при неизменном реальном доходе.
Эффекты замещения и дохода чаще всего наблюдаются вместе, т.к., например, при понижении цены товара потребитель замещает им более дорогие товары и одновременно увеличивает спрос на этот товар вследствие роста реального дохода.
Сумма двух эффектов приводит к изменению величины спроса.
Различают эффекты дохода и эффекты замены по Хиксу и Слуцкому.
Подход Слуцкого к разложению общего результата изменения цены на эффект дохода и эффект замены отличается от подхода Хикса трактовкой реального дохода. По Слуцкому выделение эффекта дохода достигается определением такого его уровня, который обеспечил бы потребителю возможность приобрести после изменения цен тот же самый набор товаров, что и до изменения, а не сохранить прежний уровень удовлетворения, как это предполагается в модели Хикса.
Выводы по Хиксу:
o методология Хикса отвечает основным положениям порядковой теории предельной полезности (потребительские предпочтения, кривые безразличия и т.п.).
o по методологии Хикса эффект замены характеризуется движением вдоль одной и той же кривой безразличия U 1 (реальный доход потребителя не меняется, т.к. он остается, на исходной кривой безразличия).
Эффект дохода по Хиксу характеризуется переходом с одной кривой безразличия на другую.
Выводы по Слуцкому:
o методология Слуцкого соответствует основным положениям количественной теории предельной полезности.
o Слуцкий опирается на наблюдаемые и регистрируемые факты поведения потребителя на рынке.
По методологии Слуцкого эффект замены характеризуется движением вдоль вспомогательной бюджетной линии.
Эффект замены всегда отрицательный: повышение цены стимулирует потребителей замещать это благо другими, относительно подешевевшими; понижение цены одного блага стимулирует потребителей увеличивать его потребление, уменьшая потребление другого блага.
Эффект дохода может быть:
o отрицательной величиной для нормальных товаров (как в нашем примере);
o положительной величиной для некачественных товаров
o н ейтрален - когда спрос на товар при изменении дохода не изменяется и эффект дохода равен нулю.
Контрольные вопросы и задания по теме:
1.Какая проблема возникает в связи с ограниченностью ресурсов?
2. Что характеризует кривая производственных возможностей?
3. О чём говорит закон замещения?
4. О чём говорит закон возрастающих альтернативных издержек?
5. Что вы понимаете под альтернативным товаром и альтернативными издержками?
6. Что вы понимаете под предельной нормой трансформации?
7. Как рассчитывается предельная норма продуктовой трансформации?
8. Могут ли следующие точки лежать на одной кривой производственных возможностей: А (18; 0), В (11; 16), С (16; 9), Е(8;15), М (7; 16), Р (0; 21)? Обоснуйте свое решение, не прибегая к построению графика КПВ.
9. Какие проблемы возникали в России в связи с конверсией военного производства, с налаживанием на предприятиях ВПК производства гражданской продукции. Всегда ли эта продукция оказывалась дешевле аналогичной, производимой на гражданских предприятиях?
10. Сформулируйте понятие производственной функции? Почему ее называют технологической функцией?
11. Что означает экономически эффективный и технологически эффективный способы производства?
12. Как рассчитывается производительность факторов производства. Приведите графическое изображение общей, средней и предельной производительности факторов производства.
13. Что отражает закон убывающей средней и предельной производительности факторов производства? Как он действует краткосрочном в долгосрочном периодах?
14. Зависят ли средний, предельный и общий продукты труда от величины используемого фирмой капитала? Если «да», то каким образом?
15. В чем проявляется проблема уровня и темпов физического и морального износа оборудования и других капитальных благ в России?
16. Сформулируйте амортизационную политику российских предприятий.
17. Как вы понимаете смысл следующих выражений: «Издержки производства не оказывали бы никакого влияния на конкурентную цену, если бы они не воздействовали бы на предложение» и «Множество бесплодных споров об «истинной стоимости» вещей возникает из-за неспособности понять, что только действиям присущи затраты и что одни и те же действия нередко означают различные затраты для разных людей»?
18. Почему в России возможно резкое улучшение положения предприятий при относительно небольших издержках (эффект увеличивающей отдачи).
19. Покажите графически и объясните, как внедрение прогрессивных форм организации производства повлияет на карту изоквант.
20. Какую программу нужно проводить предприятию, чтобы минимизировать издержи производства?
21. На конкретном примере приведите оптимальную комбинацию факторов производства.
22. Что предполагает многофакторный анализ прибыли?
23.Какие факторы влияют на благосостояние потребителя? Зависят ли эти факторы от типа экономической системы? И если да, то, каким образом применяется набор факторов, влияющих на благосостояние при переходе от одного типа экономической системы к другому?
24. Какие фирмы преобладают в современном рыночном хозяйстве: допредельные, предельные или запредельные?
25. Фирмы, производящие в себе убыток, должны обязательно всегда закрываться. Верно ли это утверждение?
26. В какой степени цель фирмы-монополиста заключается в максимизации прибыли? Всегда ли фирма-монополист должна стремиться к максимальной прибыли, а не (например) к улучшению социальных условий, спонсированию искусства или политической компании?
27. Для получения максимальной прибыли нужно продать максимально большее количество продукции. Верно ли это утверждение?
28. Является монополия «злом» или «благом» для общества? Кто выигрывает, и кто проигрывает в условиях монополии?
29. Всегда ли монополия приводит к Х-неэффективности? В каких случаях монополия способствует техническому прогрессу?
30. Почему ценовая конкуренция малоэффективна в условиях рынков с дифференциацией продукта? Каким образом можно было бы повысить значимость ценовой конкуренции в таких условиях?
31. Можно ли утверждать, что высокие расходы на рекламу тормозят развитие производства?
32. Характеризуется ли монополистическая конкуренция ограничением конкуренции? Почему «да» или почему «нет»? В каком случае мы можем говорить о преобладании конкуренции, а в каких – о преобладании монополии при исследовании монополистической конкуренции?
33. Объясните правило максимизации полезности.
ТЕМА 3.ЭФФЕКТИВНОСТЬ РЫНОЧНОЙ СИСТЕМЫ / СЛАБОСТИ (несостоятельность) РЫНКА
3.1. Эффективность выпуска или состояние рыночного равновесия.
Общее равновесие – соответствие (согласование) развития всех сфер экономической системы: спрос и предложение не только товаров и услуг, но и рабочей силы, капитала – равновесие на всех рынках + влияние политических, социальных факторов.
Основоположником теории равновесия в условиях совершенной конкуренции считается Л. Вальрас.
Весь экономический мир Л. Вальрас разделил на две группы:
1. фирмы (покупатели – на рынке факторов производства, и, продавцы – на рынке потребительских товаров);
2. домашние хозяйства (продавцы – на рынке факторов производства и покупатели – на рынке потребительских товаров).
Соответствие спроса и предложения товаров и услуг устанавливается через «нащупывание» цен (методом проб и ошибок).
Состояние равновесия предполагает наличие трех условий:
1. спрос и предложение факторов производстваравны: на них устанавливается постоянная и устойчивая цена;
2. спрос и предложение товаров и услуг равны; они реализуются на основе постоянных и устойчивых цен;






