Методические указания к решению Задачи 3

                          Общий порядок расчета

       Расчеты элементов конструкций на осевое растяжение и сжатие удобнее всего выполнить на примере простого кронштейна. О кронштейнах говорилось в Задаче 1 Контрольной работы.

В отличии от Задачи 1, где заданы углы и неизвестны длины элементов кронштейна, в настоящей задаче заданы его размеры, а углы следует определить используя тригонометрические зависимости прямоугольном треугольнике (проще всего использовать  ). В рамках задачи при определении углов разрешается округление его до 1 градуса.

 

     1. Определяем усилия в элементах кронштейна (тяге и упоре), используя геометрию кронштейна и уравнения равновесия:

             1. ∑Х = 0 и  2. ∑ Y = 0. (см.Задачу 1 контрольной работы)

Из уравнений равновесия находим величину и знак усилий.Очевидно, что тяга испытывает растяжение, а упор – сжатие, решение уравнений является подтверждением предположений.  . Будем считать тягу стальной, а упор – деревянным. В целях единообразия расчетов сечения элементов приняты круглыми и квадратными: стальные тяги круглого сечения (гладкая арматура)  или   квадратного (пруток), деревянные упоры – квадратного сечения (брус) или круглого (бревно).

 

              2. Подбираем размеры сечения стальной тяги:

а) определяем требуемую площадь поперечного сечения тяги:

 ≥  

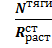
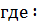
   – растягивающее усилие в тяге – кН;

 - расчетное сопротивление стали растяжению в                      зависимости  от марки  - кН / cм²  (табл.1 Приложения V).

 

б) определяем требуемый размер стороны квадратного прутка:

                              а^треб  =

Округляем требуемый  размер стороны квадрата  а^треб до размера кратного 2мм (в большую сторону) и назовем его принятым размером-   а^прин .π

Находим площадь принятого сечения стального прутка

                           А^прин  =  (а^прин)²

Очевидно, А^прин ≥ А^треб  , т.е. она принята с запасом прочности.

 

в) определяем требуемый диаметр арматурного стержня, используя формулу для определения площади круга А = , откуда

d =  при наших обозначениях   d ^треб =   .

Округляем  размер требуемого диаметра d^треб  до 2 мм (в большую сторону), назовем его принятым диаметром и обозначим -   d ^прин.

Находим площадь принятого сечения круглой арматуры

                          А^прин =     .

Очевидно, что А^прин А^треб т.е. она принята с запасом прочности.

 

  3. Проверим прочность принятого сечения

                                <

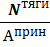где:   А^прин - принятая площадь сечения тяги см. пункт б) или в).

     

Если условие удовлетворено, прочность обеспечена. Если нет – допущена ошибка и требуется перерасчет.

4. Подбор сечения деревянного упора без учета продольного изгиба.

Порядок определения размеров сечения деревянного упора выполняется по тем же формулам, что и для стальной тяги в соответствии с      пунктом 2 со следующими изменениями: усилие   N ^тяги  заменяется на усилие N ^упора и расчетное сопротивление стали растяжению   на расчетное сопротивление древесины сжатию     табл 2 приложения V).

 

    5.Проверка прочности принятого сечения упора без учета продольногоизгиба выполняется аналогично пункту 2 с учетом пункта 3.

 

   6) Подбор сечения деревянного упора с учетом продольного изгиба

    а) определяем требуемую площадь поперечного сечения упора                                   А^треб  ≥

где: 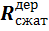    - расчетное сопротивление древесины сжатию табл.2   Приложения V.

- коэффициент продольного изгиба, предварительно принимается в пределах 0,5 … 0,7.

Размеры сечения принимается по правилам (методике), изложенным в

пункте 2, б) и в) для квадратного и круглого сечений.

 

7) Проверка прочности принятого сечения с учетом продольногоизгиба                                 

                                  ≤

где  :  φ  определяется по п. 4.1.в)

Если условие соблюдается прочность обеспечена, если нет – необеспеченна. Необходим перерасчет.

8. Определить удлинение стальной тяги

Примеры решения задач

                                   К задаче 3

   Пример 10. Подобрать сечение элементов (тяги и упора) кронштейна

              (рис. 19) по следующим данным: тяга из стали марки 235,.                        сечение подобрать в 2-х вариантах: круглое (арматура) и

               квадратное (пруток); упор из сосны 1-го сорта, сечение

               тоже в двух вариантах: квадратное (брус) и круглое 

                (бревно). Проверить прочность принятых сечений.

                Определить удлинение тяги и укорочение упора. 

      

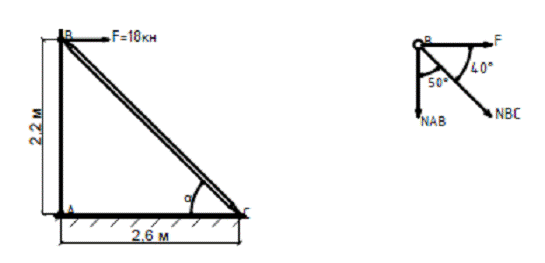
Рис. 19

 

 

Решение. Определим любой из острых углов – пусть это будет

угол АСВ  ,  обозначим его  α

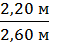                           = = 0,846.  

По таблице Брадиса (приложение IX) находим ближайшее

Значение тангенса 0,837, принимаем  α = 40^о, для которого

       Cos40⁰ = 0,766 и косинус дополнительного угла 50^о

          Cos50⁰ = 0,643.

  1. Составляем уравнения равновесия (см. рис 19, б)

         1. ∑ Х  = 0 или F + N_BC ∙ Cos 40⁰ =  0, откуда

                  N_BC = - = = - 23,5кН (сжат)

 В целях единообразия обозначений для последующих расчетов    примем N _BC = N ^сжат.

                     2. ∑ У =0    или    -   N _АВ   -   N_BC ∙ Cos50⁰  =  0 откуда                                                   

                         N _АВ = - N_BC ∙ Cos50⁰ = - (-23,5) 0,643 = 15,1 кН.

 В целях единообразия обозначений примем N _AB = N ^раст.

   Итак, усилие в тяге N ^раст = 15,1кН, усилие в упоре   N ^сжат = 23,5 кН.

 

2) Подбираем сечение тяги: N ^раст = 15,1 кН,сечение круглая арматура, сталь марки С – 235, 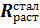 = 230 МПа = 23 кН/см²(табл.1 приложение ):

 а) определяем требуемую площадь сечения стальной тяги

   =  =   =  0,657 см²

   Определяем требуемый диаметр стержня

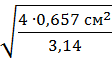=   =   =  = 0,915 см

Округляем 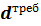 до размера кратного 2мм в большую сторону, принимаем диаметр тяги d ^прин = 1см (10 мм) или просто d для удобства дальнейших расчетов.

         3 ) Проверим прочность принятого сечения

                            ≤  

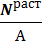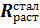
       где: = =0,785 см²,тогда

                   =   19,2 кН/см² 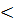 23 кН/см².

 Условие выполнено, прочность принятого сечения тяги обеспечена

.4 ) Подбираем сечение сжатого упора без учета продольного изгиба:

                          А^треб  ≥                                      

где:  = 14МПа = 1,4 кН/см² для бруса из сосны 1-го сорта (табл.2

                   приложения V) тогда  

                         А^треб ≥   =  16,8 см²

Определяем размер стороны квадратного бруса

                а^треб = 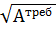 = = 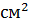4,1 см

Округляем размер стороны  бруса до 2 см в большую сторону и примем

а^прин = 6 см > а^треб = 4,1 см. Проверку п.5 можно не делать, так как очевидно, что принятая площадь А^прин = 6 ×6 = 36 см² > А^треб = 16,8 см².

Еще раз отметим, что такой расчет выполняется исключительно в учебных целях, при расчетах сжатых стержней обязательно учитывается явление продольного изгиба. По условию задачи 3 предлагается выполнить расчет сжатого упора с учетом продольного изгиба самостоятельно используя Методические указания, стр.          [ 1 ], стр.           [2].

            

6) Определяем удлинение стальной тяги и укорочение деревянного упора:

 

       а)удлинение стальной тяги        б)укорочение деревянного упора

      ∆l =                            ∆l =

где: = 15,1 кН.                         где: = 23,5 кН

                l    = 220 см                                l = 2,6м/ =2,6/0,766=3,39м

     А      = 0,785 см²                                            А = 36 см²

     Е      = 2 ∙ 1 ∙ 10⁵ кН/см²                                Е = 1 10⁴ кН/см²

                                                                                                

∆ l =  =              ∆l =  =

  = 0,022 см = 0,22 мм                         =0,019см=0,19мм

 

           

 

 

 

                                       Рис. 20

Критерии оценки решения

                                      К задаче 3

Общая оценка «зачтено», при этом предусматривается следующая дифференциация оценки.

 

Оценка «удовлетворительно (три)»:

-подобрано сечение растянутого стального элемента (тяги)

-подобрано сечение сжатого деревянного элемента (упора) без учета         продольного изгиба (пункты 1-5).

Оценка «хорошо (четыре)»:

-определено  удлиненные растянутой тяги

      -определено укорочение сжатого упора (пункты 1-7).

Оценка «отлично (пять)»:

 - подобрано сечение сжатого упора с учетом продольного изгиба

 -выполнена проверка прочности упора с учетом продольного изгиба (пункты 1

                    Задача 2. Подбор сечения балки.

     Краткие теоретические сведения

                  Внутренние усилия и напряжения в брусе при изгибе

     При изгибе бруса в любом сечении бруса возникает два внутренних усилия ( без доказательства), которые называются: изгибающий момент - М_х  и поперечная сила – Q_{х .} Изгибающий момент М_х  (в дальнейшем будем называть его просто М_х) возникает в  следствии изгиба бруса под действием внешних нагрузок, (явление известное нам из обычной жизни больше  как «прогиб» и «выгиб»). Поперечная сила Q_x  (или в дальнейшем просто Q_x)возникает в результате «как бы среза»  двух смежных сечений  в брусе  подробнее см. стр.       [1]. Индекс х указывает на то, что сечение рассматривается на каком-то расстоянии х  от одного из концов (обычно левого) бруса (рис. 20).

 

               

 

М_х в любом сечении бруса равен сумме моментов всех внешних сил, расположенных только слева (или только справа) от этого сечения.

            Определение понятия «момент» дано в методических указаниях к Задаче 2.Поскольку момент может оказывать два противоположных действия на брус (прогиб-выгиб), для него устанавливается знака «плюс»

«минус».  

            М_х  считается положительным «+», если внешние силы, расположенные слева от рассматриваемого сечения стремятся повернуть брус по часовой стрелке, и отрицательным «--», если против

часовой. Для правой части – наоборот.

          Q_x в любом сечении равна сумме проекций всех сил, расположенных только слева (или только справа) на ось 0-у. Q_x c читается

положительной, если силы расположенные слева направлены вверх, и отрицательной- если вниз. Для правой части – наоборот. Понятие «проекции силы на ось»  дано в методических указаниях к Задаче 1.

 

     М_х  и Q_x   необходимы при расчете бруса на прочность при изгибе, но

при этом пользоваться ими не удобно. Поэтому для записи условия прочности используют следующую формулу:

                                                  𝛔 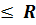     _изг                                        a)

где: R _изг  - расчетное сопротивление материала изгибу;

       σ (греч. сигма) – нормальное напряжение в материале при изгибе:

                                                      σ  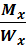   =                       b)

где: M_x  – изгибающий момент (см. выше);

     W_x – момент   сопротивления сечения, связан с геометрией сечения,

                т.е. с размерами и формой поперечного сечения, от которых зависит прочность бруса наряду с прочностными характеристиками материала, из которого он изготовлен.

       Условие а) с учетом формулы б) можно записать в следующем

 виде:                                          _изг                               в)

 Учитывая, что W_x связан с размерами и формой сечения,

формулу в) используют для определения необходимых размеров сечения для обеспечения его прочности:

                            W_x .                             г)

Между W_x и размерами сечения существуют математические зависимости. Определив   W_x, можно найти его размеры (подробнее см

Методические указания к задаче 4, а также стр.     [1].

Практические задачи

     Расчет простых балок на прочность и жесткость

 Простые балки - лучший практический материал для применения теоретических знаний.О простых балках уже говорилось в методических указаниях к задаче 2, целью которой было определение опорных реакций.

Кроме общепринятого способа определения опорных реакций (с помощью уравнений равновесия   ∑М_А = 0 и ∑М_В =0),     которому была посвящена Задача 2, возможен еще один – это частный случай, когда схема самой балки и нагрузка, действующая на нее, имеют ось симметрии. В этом случае и опорные реакции тоже будут симметричными и равными друг другу

                           R_A   = R_B =

 Именно с такими балками придется иметь дело в Задаче 4

      Для подбора сечения балки необходимо знать наибольший изгибающий момент, М_макс возникающий в балке. Существует несколько способов её определения (см. стр.      [1]. Используем самый простой: разбиваем балку на участки через 1,0м (или 0,5 м- чем меньше, тем лучше),

Затем определяем изгибающие моменты во всех этих точках. Откладываем полученные значения от какой-то нулевой линии в определенном масштабе, и результате получаем график изменения М_х  по всей длине балки..Этот график называется эпюрой изгибающих моментов. Эпюра   М_х   дает возможность с достаточной точностью указать в каком сечении балки возникает наибольший момент   М_макс . Если обеспечить прочность балки в сечении с М_макс, то балка будет прочной по всей ее длине.

           После определения М_макс  находят размеры сечения балки используя условие прочности  :

                                           W_x

Подробнее о порядке об определении размеров сечения балок изложено в Методических указаниях к Задаче 4.

                Методические указания к решению Задачи 4

    Построение эпюры М_х  и подбор сечения балки

     1. Определяют опорные реакции. Поскольку в задании приведены схемы балок с нагрузками, которые имеют ось симметрии относительно середины балки, опорные реакции будут равны между собой и каждая равна половине всей нагрузки, действующей на балку:

                                R_A = R_B   =

       2) Определяем изгибающие моменты в точках балки. Разбиваем балку на участки через 1,0 м и обозначим их границы   С, А, Д, Е, К, L, Р, В, S.

 Определяем  величину и знак моментов каждой из точек: М _С, М_А,М _Д,М _Е

  и М_К. Моменты в точках   L, P, B, S будут равны моментам в точках C, A, D, E вследствии свойства симметрии балки, поэтому их можно не определять, а просто воспользоваться ранее найденными.

       3).После определения величины и знака изгибающего момента в

каждой точке строят эпюру (график) изгибающих моментов, откладывая полученные значения в каком – либо масштабе от нулевой линии с учетом знаков. В строительной практике положительные значения откладываются вниз от нулевой линии, а отрицательные – вверх.

При этом следует учесть следующие:

 - если на участке между  точкам нет нагрузки, то эпюр -М_Х прямая наклонная к оси линии;

- если на участке между характерными точками есть равномерно распределенная нагрузка, то эпюр М_Х - кривая, точнее парабола, обращенная выпуклостью вниз.

В частном случае действия симметричных нагрузок эпюра М_Х будет тоже симметричной относительно середины балки, т.е если построена эпюра для левой части балки,то на правой половине балки  эпюру М_х   можно построить  без вычислений – симметрично левой.

       4 Находим на эпюре   М_х  точку, в которой значение момента является наибольшим - М_макс.

 

5. Подбираем сечение балки из стального прокатного двутавра:

а) находим требуемый момент сопротивления балки :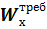

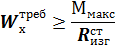
где: 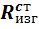- расчетное сопротивление стали изгибу см. табл 1. Приложения V.

б) по найденному 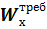 по табл. 3 Приложение 1 находим номер двутавровой балки 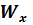, - ближайшие значение к 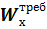- ближайшее из двух.

в) проверим прочность принятого сечения

                                    ≤

Если условие удовлетворено, то это значит, что прочность обеспечена.

6. Подбираем сечение балки из деревянного бруса

а)  находим требуемый момент сопротивления балки :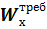

 

                                           =

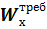где: 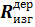 - расчетное сопротивление древесины изгибу см табл2. Приложения V.

б) по найденному 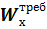 находим размеры сечения b и h. Для этого следует задаться отношением сторон    h / b = 1,5 …2,0, т.е. высота сечения должна быть в 1,5 … 2,0 раза больше ширины. Это соотношение взято из сложившийся практики.

 

Из табл. Приложения 2 находим, что момент сопротивления для прямоугольного сечения  равен:

                                           = ,

 

 

Подберем размеры сечения деревянной балки в двух вариантах:

           h = 2 b и h = 1,5 b.  

             

Если h =2 b,    то   W_X =  = , откуда

                         b = .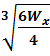

Округляем   b   до размера кратного 2 см в большую сторону, принимаем h =2  b  и округляем его тоже как b.

 

Если h = 1,5 b,   то           W _X   =  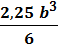 = , откуда

                                     b =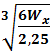  

округляем «b» до размера кратного 2 см в большую сторону, находим

h   и округляем.

в) проверим прочность принятого сечения

                                         ≤      

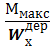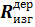
где:   - момент сопротивления деревянной балки прямоугольного сечения с округленными размерами   b и h  по п. 6,б):

                                      = .

Если условие удовлетворено, то прочность обеспечена.

           Определение прогиба балки и расчет на жесткость.

 

Определение прогибов и построение деформированной схемы балки – сложная математическая задача с использованием зависимой высшей математики.

Вместе с тем, целый ряд задач на определение прогибов для некоторых несложных схем балки с нагрузкой возможно по готовым формулам по табл. Приложения.

                   

                  

Примеры решения

                           К задаче 4      

 

 Пример 11 Подобрать сечение балки показанной на рис.21, а) по следующим данным: q ₁ = 3 кН/м,   q ₂ = 2,5 кН/м,   F ₁ = 0,5 кН;   F ₂ = 1,5 кН.   Материалсталь С – 235. Проверить: выдержит эту нагрузку деревянная балка c размерами сечения b = 10 см и   h = 20 см из сосны 1-го сорта.

Рис. 21.

Решение.

1.Определяем опорные реакции   R_A и R _{В .} В  следствии симметрии схемы балки и нагрузки опорные реакции R _A и R _В равны между собой и каждая равна половине всей нагрузки, действующей на балку:

 

R _A  = R _В =  =  =  = 13,25 кН.

 

2. Определяем изгибающие моменты в точках    С,А,Д,Е,К рассматривая левую часть балки:

М_С = 0

М_А = - F₁·a  –  q₁·a  =  -0,5·1,0  –  3 кН / м ·1,0·   =   -2 кН · м

М_Д = - F₁ · 2a  –  q₁ · a · 1,5 а  +  R_A · a  –  q₂ a ·   =

 - 0,5 · 2 · 1  -3 · 1 · 1,5 · 1  +  13,25 · 1  -  2,5 ·1 · =   6,25 кН · м

M_E = -F₁ ∙3  –  q_{1 ∙} a ∙ 2,5 a  +  R_a∙ 2  –  q₂∙ 2a∙ a  =

 - 0,5 ∙ 3 ∙ 1  – 3 ∙ 1 ∙ 2,5 ∙ 1  +  13,25 ∙ 2  – 2,5 ∙ 2 ∙ 1  =   12,5 кН · м

M_K = - F₁ ∙ 4  – q_{1 ∙} a ∙ 3,5 a  +  R_a∙ 3  –  q₂∙ 3a ∙1,5 a  –  F₂ ∙ 1  =

- 0,5 ∙ 4 – 3 ∙ 1 ∙ 3,5 ∙ 1 + 13,25 ∙ 3 – 2,5 ∙ 3 ∙ 1,5 ∙ 1 – 1,5 ∙ 1 = 14,5 кН·м

Учитывая свойство симметрии балки и нагрузки величины моменты в точках   L, P, B, S  симметричны соответственно Е, Д,А, С:  

          M_L   = 12,5 кН·м,    M_P   = 6,25 кН·м,   M_B   = -2 кН·м,   M_S = 0.

3. По найденным значениям  стоим эпюру М_х (рис. 21 б).

 

4. Из эпюры М_х  видно. что наибольший изгибающий момент возникает  в точке   К   М_макс   =   M_K  = 14,5 кН·м   или  1450 кН·см.

5. Подбираем сечение балки из стального прокатного двутавра:

а) находим требуемый момент сопротивления W_X ^треб:

             W_X ^треб   =  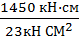 =    =  63,04 см³

где: 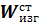  =  23 кН/ см²  расчетное сопротивление стали С – 235 (Таб.1 Приложения.)

б) п о  найденному   W_x ^треб      находим номер двутавровой балки  по табл.3 Приложения 1, в которой он обозначен W_x. Принимают ближайшее значение больше требуемого:

                    I  № 14  c W_X = 81.7 см ³> 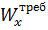 = 63,04 см ³

 

6. Проверим, выдержать заданную нагрузку деревянная балка прямоугольного сечения размерами b × h = 10×20 см, где b - ширина сечения, h - высота (рис. 22а)

Балка будет прочной если удовлетворено условие прочности

                                   ≤

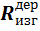
где  : М_макс  = 1450 кН·см

               W _х – момент сопротивления сечения:

                         W_X =  =   = 667 см³

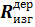      = 1,4 кН/cм² расчетное сопротивление пиленой древесины изгибу - табл. 2. Приложение..

Подставим полученные числовые значения в условие прочности

                = 2,17 кН/см² 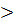 1,4 кН/см²

Условие прочности не выполнено, значит деревянная балка с размерами сечения 10см 20 см не выдержит заданную нагрузку.

Рис.22

Проверим: будет ли обеспечена  прочность балки состоящей  из двух спаренных брусьев   2(10 см как показано на рис. 22, б.

Момент сопротивления W _х     увеличится в два раза

              W_{x 2} = 2 W_{x 1} = 1334 см³ , тогда

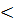                         ² 1,4 кН/см²

     Условие прочности выполнено, прочность обеспечена.

 

            7. Построить эпюру поперечных сил Q_X

Рис.23

8. Определение прогиба в середине балки в точки К

Прогиб в точке К равен сумме прогибов отдельных видов нагрузок:

f_{q 2} =  – прогиб от нагрузки q ₂ – схема …,

f _{1 f 2} =  – прогиб от силы f ₂, приложенной в середине пролета - схема …, f _{2 f 2} = … - прогиб двух сил F ₂, приложенных в третях длины балки - схема … f _ма =  - выгиб от момента на опоре.

f _ма, где М_а = - F ₁ · a - q ₁ · a

E - модуль деформации стали Е= 2·10 кН/см²

J_X - момент инерции в зависимости от номера двутавра ГОСТ. Приложение1, табл.1

J_X = f_{q 1} + f _{1 f 2} + f _{2 f 2} - f _ма

Проверка балки на тяжесть

f _к ≤ [ f ]

[ f ] = 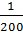l = 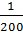·600 = 3 см.

 

           

Задание для задачи 4

 Подобрать сечение балки для одной из схем, приведенной на рис. 24. по следующим данным двух вариантах:

1) Сталь с – 235

2) Древесина: сосна 1-го сорта, прямоугольного сечения с отношением сторон   h / b = 2.

3)  Построить эпюру Q

4) Определить прогиб

 

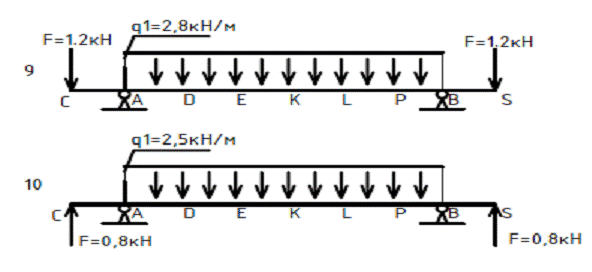
Рис.24

 

 

Критерии оценки решения

                                   К задаче 4

 

 

Общая оценка «зачтено». При этом предусматривается следующая дифференциация оценки.

Оценка  «удовлетворительно (три)»:

-построена эпюра   М_х

-подобрана сечение балки в двух вариантах:

 а) прокатного стального двутавра  

   б)деревянной балки прямоугольного сечения из сосны 1-го сорта с отношением h / b = 2,0 ( пункты1-7 ).

Оценка «хорошо  (четыре)»:

-построена эпюра Q_X (п. 1-8).

Оценка «отлично (пять)»:

             -найден прогиб в середине балки;             

             - проверено условие жесткости, если f _доп = 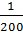  l (п. 1-9)

                (вариант стальной балки).

 

.

 

 

Вопросы для самопроверки

                                        К задаче 4

 

1. Что такое поперечный изгиб?

2. Какие внутренние условия возникают в поперечных сечений балки при поперечном изгибе?

3. Как вычисляют изгибающий момент М_Х в любом сечении балки по ее длине?

4. Каково правило знаков при определении М_Х?

5. Как вычисляют поперечную силу Q_X в любом сечении балки по ее длине?

6. Что такое эпюра М_Х и как она строиться?

7. Что такое эпюра Q_X и как ее строиться?

8. Какие зависимости между нагрузками и эпюры М_Х?

9.Какие зависимости между нагрузками и эпюры Q_X?

10. По какой формуле определяют нормальные напряжения G?

11. Как выглядит условие прочности при изгибе?

12. Как выглядит формула для определения площади сечения балки?

13. Как связана площадь сечения балки А с размерами и формой поперечного сечения?

14. В чем заключается проверка прочности сечения?

15. Как можно найти прогиб в балке?

16. В чем заключается проверка жесткости балки?