общий порядок расчета
1. Заменяют распределенную нагрузку q её равнодействующей Rq, которая является сосредоточенной силой. Для равномерно распределенной нагрузки равнодействующая равна произведению интенсивности нагрузки q на длину участка l 1, на котором она действует, т.е. Fq = ql 1 ( рис.13).
Рис.13.
2. Обозначают опоры. Общепринято обозначать их буквами A и B.
3. Освобождаются от опор и заменяют их действие на балку реакциями. Реакции опор будут только вертикальными. Обычно их направляют вверх (против действия основной нагрузки). Реакцию опоры A будем обозначать RA, опоры B – RB вместо обозначений V A и V B .
4. Составляют уравнения равновесия вида:
1. ∑ MA = 0; 2. ∑ MB = 0.
Решают эти уравнения и находят реакции RA и RB.
Напомним, что моментом силы относительно точки называется произведение этой силы на плечо - кратчайшие расстояние от этой точки приложения силы (в общем случае до линии действия силы).
Если сила стремиться повернуть балку относительно рассматриваемой точки по часовой стрелке, то будем считать ее момент положительным, а если против – отрицательным. Сосредоточенный момент не умножается на расстояние до опоры, а правило знаков остается тем же, что для момента силы.
5.Выполняют проверку решения. Для этого составляют уравнение равновесия:
∑ Y = 0.
Оно означает, что сумма проекций всех сил действующих на балку (в том числе и опорных реакций) на ось 0 - у должна быть равна нулю.
Если это условие (уравнение) удовлетворенно, то реакции найдены правильно, а если нет, то в решении допущена ошибка.
При составлении уравнений равновесия наибольшую трудность представляет распределенная нагрузка, положение, которой относительно опор может быть самым различным. При всем разнообразии случаев действия распределенной нагрузки их можно свести к шести, показанным на рис. ….. стр.75 [1].
5. Выполняют проверку правильности решения вторым аналитическим способом, а именно: суммы моментов всех сил, действующих на балку только слева и сил действующих только справа от любой точки балки должны быть по абсолютной величине одинаковыми. В целях единообразия решения задачи 2 такой точкой выбрана середина пролета (расстояние между опорами) и обозначена буквой C . Это условие математически можно записать следующим образом:
.│ ∑МСлев │ = │ ∑МСправ |.
Такая проверка не выполняется в примерах методической разработки, и её предлагается выполнить самостоятельно.
Примеры решения задач
к задаче 2
Пример 7. Определить опорные реакции балки, изображенной на рис. 14, а.
Решение. 1. Заменяем распределенную нагрузку равнодействующей. На балку действуют нагрузки разной интенсивности, поэтому для каждой из них найдем равнодействующую:
Fq 1 = q 1 l 1 = 20 ∙ 4,5 = 90 кН; Fq 2 = q 2 l 2 = 15 ∙ 3 = 45 кН,
где l 1 = a + b = 1+3,5 = 4,5 м; l 2 = d + d = 1,5 +1,5 = 3 м.
Укажем расстояния от этих сил до каждой из опор (рис. 14 б).
2 Обозначим опоры А и В.
3 Укажем опорные реакции VA и VB. Обычно рис. 6, а и б совмещают в одном
4 Составляем уравнения равновесия. Первое уравнение для нашей задачи примет вид
Fq1 (l1/2 - a) – F (b + c) + Fq2 l – VB l – M = 0,
откуда
VB = [ Fq1 (l1/2 - a) – F (b + c) + Fq2 l - Fq2l – M ] /l = ?
= 
= 37,1 кН.
Второе уравнение примет вид
VA l – Fq1 (d + c + l1/2) + F d – M = 0,
откуда
VA = [ Fq 1 (d + c + l 1 /2) – F d + M )] / l =
= 67,9 кН.
5 Выполним проверку, используя уравнения ∑ Y = 0, которое примет вид
VA – Fq 1 + F + VB – Fq 2 = 0
или
67,9 – 90 + 30 + 37,1 – 45 = 0,
откуда 135 – 135 = 0
Условие удовлетворено, значит реакции определены правильно.
Ответ: VA = 67,9 кН, VB = 37,1 кН.
Пример 8. Определить опорные реакции балки, показанной на рис. 15.
Рис. 15
Решение. 1. Определим опорные реакции балки. Составим уравнения:
1. ∑ MA = 0; 2. ∑ MB = 0.
Из первого уравнения найдем VB:
- F (a+b) + q (b + c) 
VB (c+d) – M = 0
или
-15 ∙ 2 + 20 ∙ 6 ∙ 2 – VB ∙ 7 – 25 = 0,
откуда VB =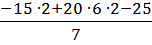 
= 26,4кН.
Из второго уравнения найдем VA:
- F (a+b+c+d) + VA (c+d) – q (b+c) 
– M = 0
или -15 ∙ 9 + VA ∙ 7 - 20 ∙ 6 ∙ 5 – 25 = 0,
откуда VA = 
= 108,6 кН.
Выполним проверку:
∑ Y = VA + VB – F – q (b + c) = 0
или 108,6 + 26,4 – 15 – 20 ∙ 6 = 0,
откуда 135 – 135=0.
Ответ: VA = 108,6 кН, V В = 26,4 кН.
Задание для задачи 2
Определить опорные реакции балки, приведенной на рис. 16. Выполнить проверку правильности определения опорных реакции двумя способами:
1) ∑ Y = 0;
2) 
MC лев = ∑ MC прав, где С – середина расстояния между опорным (на рис. не показана)
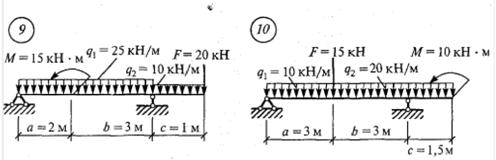
Рис.16
Критерии оценки решения
Задача 2
При общей оценке «зачтено» предусматривается следующая дифференциация.
Оценка «удовлетворительно» (три):
-составлены уравнения равновесия ∑ MA = 0; ∑ MB = 0, без ошибок (выполнены пункты 1 - 4).
Оценка «хорошо» (четыре):
-составлено проверочное уравнение ∑ Y = 0 (выполнены пункты 1 - 5).
Оценка «отлично» (пять):
-составлены уравнения суммы моментов всех сил, действующих слева и справа от т. С, - середины расстояния между опорами. (выполнены пункты 1 - 6):
│∑МСлев│ = │∑МСправ│.
Задача 3: Подбор сечения элементов кронщтейна.
Краткие теоретические сведенья о расчете на прочность растянутых и сжатых элементов.
а) Условие прочности растянутого элемента цельного сечения имеет вид (без вывода):
≤ R раст а)
где: R раст – расчетное сопротивление материала растяжению (на что указывает нижний индекс), приводиться для различных материалов (металл, дерево и др.) в приложении V, табл.1,2;
А – площадь поперечного сечения: для простых геометрических фигур в Приложении II, для профилей проката - в приложении I.
Условие прочности а) позволяет решать задачи на подбор сечения растянутого элемента:
А ≥ 
б)
По найденной площади подбираются форма и размер сечения.
б) Условие прочности сжатого элемента цельного сечения без учетаявления продольного изгиба имеет вид (без вывода):
= R сжат в)
Подбор сечения сжатого элемента можно выполнить по формуле:
А ≥ 
г)
Где: R c жат и А находятся аналогично R раст и А.
Круг элементов, в которых не возникает продольного изгиба ограничен. Поэтому он допускается только в учебных целях.
На практике при сжатии обязательно учитывается явление продольного изгиба (выпучивание) стержней.
в) Условие прочности и подбор сечения сжатого элемента цельного сечения с учетом продольного изгиба (без вывода) имеют вид:
≤ R сжат д)
А ≥ 
е)
где : R сжат и А - те же, что в пункте.б)
φ – коэффициент продольного изгиба.
Значение коэффициента продольного изгиба φ можно определить по. приложению IV в зависимости от гибкости стержня, обозначаемой буквой λ (лямбда).Не останавливаясь на математических обоснованиях, укажем, что гибкость определяется по формуле
λ = l 0 / i,
где : l 0 – расчетная длина стержня;
i – радиус инерции сечения
В свою очередь l 0 и i тоже определяются по формулам:
-расчетная длина стержня
l 0 = μ l,
где: μ – коэффициент, зависящий от способов закрепления концов стержня (определяется по приложению VII);при шарнирном
закреплении верхнего и нижнего концов стержня μ =1
(во всех заданиях к задаче 2 принимается μ = 1);
l – геометрическая длина стержня, т.е. её фактическая длина
-радиус инерции сечения имеющего две оси симметрии,
например, для круга или квадрата, он равен
i= 
,
где: I – момент инерции сечения стержня (приложение )?
А – площадь сечения стержня (приложение I и II).
Обычно при расчете колонн коэффициент продольного изгиба φ принимают равным 0,5 … 0,8. У длинных сжатых элементов с небольшим сечением опасное напряженное состояние наступает при очень небольших нагрузках, поэтому вводят понятие придельной гибкости λпред, которая не должна быть превышена, т.е λ ≤ λпред. Значения предельной гибкости, приводимые в СН и П, зависят от ряда причин. Об этом надо помнить, но при выполнении задачи 2 мы не будем принимать во внимание λпред.
Кроме расчета на прочность, очень часто приходись вести расчет по деформации, для чего необходимо определять удлинение или укорочение стержней.
г) определение удлинения (укорочения) ∆ l растянутых (сжатых) стержней выполняются на основании закона Гука:
∆ l = 
где: ∆ l – удлинение (укорочение) стержня (см)
N – растягивающее (сжимающее) усилие в стержне (кН)
l – длина стержня (см)
A – площадь поперечного сечения (см2)
E – модуль деформации материала из которого изготовлен стержень. Величина модуля определяется экспериментально и равен:
для стали - Е = 2 ∙ 105 кН/см2 ?
для дерева - Е = 1 103 кН/cм2.
Вопросы для самопроверки
К задаче 3
1. Как можно охарактеризовать центральное растяжение элемента?
2. Чем растяжение отличается от сжатия?
3. Как выглядит условие прочности при осевом растяжении?
4. Как выполняется расчет на подбор сечения растянутого элемента?
5. Что такое R раст? Как оно определяется?
6. Как связаны А с размерами и формой поперечного сечения элемента?
7. Как выглядит условие прочности при осевом статик без учета продольного изгиба?
8. То же с учетом продольного изгиба?
9. Как называется коэффициент φ?
10. Как определить коэффициент φ?
11. Чем отличаются φ пред и φ?
12. Как записывается и как формируется закон Гука при растяжении (сжатии)?
13. Объясните значение каждого из символов, входящих в формулу закона Гука?
