Краткие теоретические сведения.
Момент силы относительной точки. Пара сил.
Моментом силы относительно точки называется произведение величины (модуля) этой силы F на кратчайшее расстояние от этой точки до линии действия силы. Это расстояние принято называть плечом и обозначать буквой h (рис. 8).
Момент силы обозначают буквой M и в общем случае определяют по формуле: M 0 = ± F h.
При этом обязательно указывается, относительно какой точки определяется момент (в нашем случае относительно точки О).
Если сила стремиться повернуть брус (тело) по часовой стрелке относительно рассматриваемой точки тела, то момент считается положительным (перед ним ставят знак «плюс», хотя чаще всего этот знак опускают), а если против часовой, то отрицательным (перед ним ставят знак «минус»).
Если на тело действует несколько сил, то вращательный эффект их на тело определяется как алгебраическая сумма моментов.
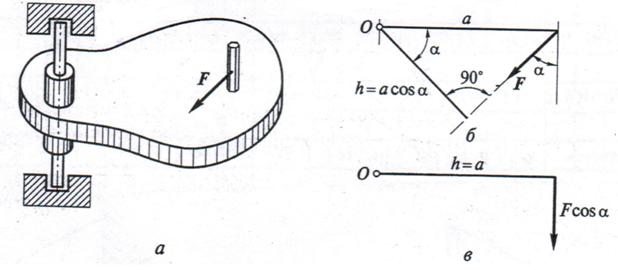
Рис. 8. Момент силы относительно точки:
а – сила, стремящееся повернуть тело; б, в – определение плеча силы.
Пара сил - это система двух параллельных сил, равных по модулю и направленных в противоположные стороны. Их иногда называют системой двух параллельных, но противоположно направленных, сил, а чаще всего просто парой сил. Воздействие пары сил на тело показано на рис. 9 а. Оно схоже с воздействием одной силы относительно оси (см. рис. 8 а), но имеются существенные отличия.
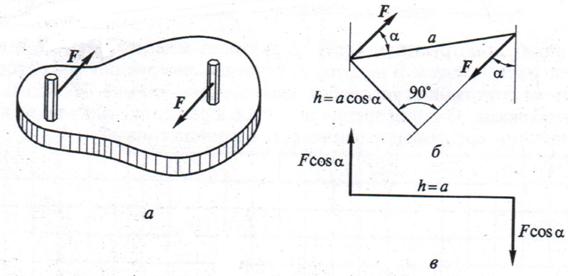
Рис. 9. Момент пары сил:
а – пара сил, стремящаяся повернуть тело; б, в – определение плеча пары сил.
Одиночная сила может оказывать вращательное воздействие на тело только при наличии какой-то связи, например шарнира или оси. Если таких связей нет, она вызывает поступательное движение тела. Пара сил оказывает вращательное воздействие на совершенно свободное тело, чего не может сделать сосредоточенная сила.
Примеры решения задач
на усвоение теоретических знаний
Пример 5. Определить сумму моментов сил F 1, F 2, F 3 и F 4 относительно точки О (рис. 10 а), если F 1 =5 кН, F 2 = 6 кН, F 3 = 2 кН, F 4 = 1 кН, h 1 = 4 м, h 2 = 3м.
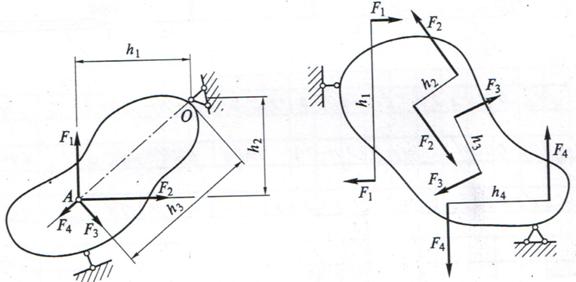а) б)
Рис. 10
Решение. Находим плечи для сил F 3 и F 4:
h =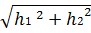 
= 
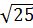= 5м, h 4 = 0.
Определяем сумму моментов сил:
∑ M O = F 1 h 1 – F 2 h 2 – F 3 h 3 + F 4 h 4 = 5 кН ∙ 4 м – 6 кН ∙ 3 м – 2 кН ∙ 5 м +
+1 кН ∙ 0 = 20 кН ∙ м – 18 кН ∙ м – 10 кН ∙ м + 0 = - 8 кН ∙ м.
Ответ: ∑ M O = - 8 кН ∙ м.
Пример 6. Определить сумму моментов пар сил (рис 10 б), если F 1 =1 кН, F 2 = 5 кН, F 3 = 3 кН, F 4 = 4 кН, h 1 = 3,5 м, h 2 = 0,5 м, h 3 = 1,5 м, h 4 = 2,5м.
Решение. Определяем сумму моментов пар:
∑ M О = F 1 h 1 – F 2 h 2 + F 3 h 3 - F 4 h 4 = 1 кН ∙ 3,5 м – 5 кН ∙ 0,5 м + 3 кН ∙ 1,5 м - 4 кН ∙ 2,5 м = 3,5 кН ∙ м – 2,5 кН ∙ м + 4,5 кН ∙ м - 10 кН ∙ м = - 4,5 кН ∙ м.
Ответ: ∑ M О = - 4,5 кН ∙ м
Практические задачи
Определение опорных реакций простых балок
В Статике как разделе Механики рассматриваются несвободные тела (проще неподвижные), свобода которых ограничивается специальными устройствами, называемыми связями. Наиболее распространенным примером такой связи является опорный стержень – это жесткий (чаще всего очень короткий) стержень, прикрепляющий рассматриваемое тело какому –либо неподвижному телу (Земле или другому телу) с помощью приспособлений называемых шарнирами (рис.11, а.б,в).
Не останавливаясь на доказательной части, скажем, что наименьшие число опорных стержней, которые могут обеспечить неподвижность телу, - три как показано на рис.11.
Как уже отмечалось, в Статике рассматриваются бесформенные тела, на практике реальные тела как правило имеют правильную геометрическую форму (рис.11, г)
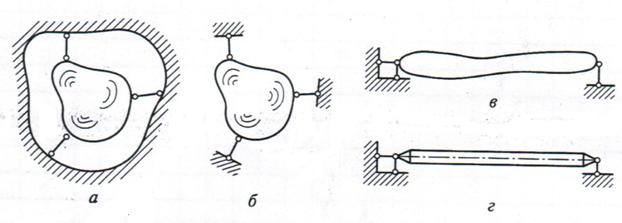
Рис. 11 Примеры крепления тел к основанию с помощью трех опорных стрежней:
а – крепление бесформенного тела; б- то же, при идеализированном изображении основания; в – крепление длинного бесформенного тела; г - крепление призматического бруса.
Конструкцию, показанную на рис.11, г называют простой балкой на двух опорах. Левую опору с двумя опорными стрежнями, называют, шарнирно – неподвижной, а левую опору с одним опорным стрежнем - шарнирно - подвижной.
На опоре А возникает две опорные реакции: V A и HA, а на опоре В -одна V B (рис.12,б) при действии произвольной нагрузки (в рассматриваемых случаях произвольной системой сил считается наличие наклонных сил)
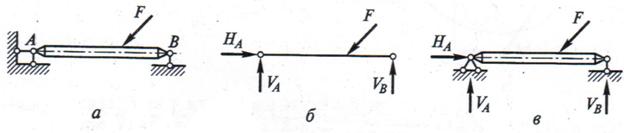
Рис. 12. Простая балка на двух опорах:
а – схема балки; б – схема сил и реакций; в – вариант изображения балки с шарнирно - неподвижной опорой.
При действии только вертикальных сил (наклонные силы отсутствуют), возникают только вертикальные опорные реакции VA и VB (т.е. H A = 0), которые чаще обозначают RA и RB.
Опуская доказательную часть примем,что при действии наклонных сил на балку необходимо иметь три уравнения, чтобы найти V A, HА и V B:
1. ∑ MA = 0; 2. ∑ MB = 0; 3. ∑ X = 0.
При действии только вертикальных сил возникает только две опорные реакции : V A и VB (или R A и R B ) поэтому достаточно иметь два уравнения:
1. ∑ MA = 0; 2. ∑ MB = 0.
При этом уравнение ∑ У = 0 можно использовать для проверки решения.
Вопросы для самопроверки.
К задаче 2
1. Что называется моментом силы относительно данной точки?
2. Как определяется плечо для каждой нагрузки, действующей на балку при составлении уравнений равновесия?
3. В каком случае момент силы относительно точки равен нулю?
4. Каково правило знаков при составлении уравнений равновесия?
5. Как определяется плечо для каждой нагрузки, действующей на балку при составлении уравнений равновесия?
6. Как обозначаются опорные реакции балки?
7. Какие уравнения равновесия необходимо составить для определения опорных реакций?
8. Какие уравнения равновесия можно использовать для проверки решения задачи об определении опорных реакций аналитическим способом?
