Код – это совокупность символов в представлении информации. Каждому знаку соответствует определённая комбинация нулей и единиц (бинарное кодирование).
Простой код – если все его символы используются для представления информации.
Равномерный код – если все его слова имеют одинаковое количество разрядов.
Существуют коды обнаруживающие ошибки и коды, обнаруживающие и исправляющие ошибки.
Как правило, при передаче информации используется избыточность – не все разряды используются для передачи информации, не все 2n (где n количество разрядов) комбинаций используются для её представления.
Разделяют разрешённые и запрещённые комбинации. Появление запрещённых комбинаций – ошибка передачи информации.
В теории кодирования используется понятие кодового расстояния (расстояние Хэмминга).
d – кодовое расстояние – это число разрядов, по которым отличаются две кодовые комбинации.
В этих двух четырехразрядных кодовых комбинациях d=2.
Рассмотрим двухразрядную информацию.
При различных ошибках (типа инверсии разряда) можно получить различные комбинации, причём они входят в исходное множество комбинаций. Поэтому по виду комбинации нельзя обнаружить ошибку. Необходимо, чтобы при возникновении ошибки полученные коды не входили в число используемых.
Чтобы обнаружить ошибку необходимо, чтобы выполнялось следующее неравенство:
dmin ³ t +1,
где t – кратность ошибок, а dmin – минимальное кодовое расстояние.
Здесь уже можно обнаружить ошибку, но нельзя её исправить. Исправить ошибку, значит, по виду принятой комбинации установить, какая истинная комбинация передавалась.
Для исправления необходимо: dmin³2t+1 (рис. 83).
Рис. 83. Принцип исправления ошибок
От каждой из четырех комбинаций, указанных на рис. 83, ошибочная комбинация с t-кратной ошибкой отличается в t разрядах, поэтому необходимо, чтобы сами ошибочные комбинации отличались друг от друга хотя бы в одном разряде, иначе восстановить передаваемую информацию невозможно. Например, рис. 84 иллюстрирует возможные ошибки при передаче трехразрядной информации.
Рис. 84. Возможные ошибки при передаче трехразрядной информации
и некоторые кодовые расстояния
Примеры кодов.
1. Код с проверкой четности.
| x2 | x2 | k |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
где k – контрольный разряд, чтобы сумма единиц была четной, либо нечетной. Это – контроль по четности (нечетности). В настоящее время широко применяется в стандартных микропроцессорах (ранее – только в особо ответственных вычислительных системах, например, военных).
В приемнике формируется контрольный разряд с помощью элемента сложения по модулю 2 (рис. 85).
Рис. 85. Передатчик и приемник информации с контролем по нечетности на основе элементов сложения по модулю 2 с инверсией
2. Коды с простым повторением – это коды, в которых повторяется кодовая комбинация.
3. Корреляционные коды.
В таких кодах используются дополнительные символы для представления информации:
0®01
1®10
4. Равновесные коды.
Характеризуются тем, что каждая комбинация содержит одинаковое количество нулей и единиц. Например, 2 из 5:
01100®0
11000®1
10100®2
10010®3
01010®4
00110®5
10001®6
01001®7
00101®8
00011®9
Существуют также систематические коды, где контрольные разряды отделены от информационных. К ним относятся коды Хэмминга.
Кодирование по Хэммингу
В ряде случаев для контроля функционирования схем реализации ПФ используют прямое сравнение, т.е. сравнивают реакции на схемах. Кроме того, применяются: прямое дублирование со сравнением результатов, троирование.
В своё время широко применялся контроль по модулю, эффективный при арифметических операциях. Используются классы эквивалентностей чисел по модулю.
|1|5=|6|5=|11|5 – сравнимы по модулю.
Контроль по нечётности – это контроль по модулю 2.
Коды Хэмминга – это кодирование с использованием нескольких групп контроля по модулю 2.
Помехоустойчивое кодирование по Хэммингу – обеспечивает обнаружение и исправление ошибок при передаче информации (контроль передачи информации).
В кодовом слове всего m разрядов, где m=n+k, n – количество информационных разрядов, k – количество контрольных разрядов.
Используется контроль по нечетности, причем формируется несколько групп контроля по нечетности.
Пример. Передается четырехразрядная информация:
Количество контрольных разрядов должно быть таковым, чтобы можно было закодировать как информационные разряды, так и сами контрольные.
В нашем случае: n=4, k=3. Разместим передаваемую информацию в секторах диаграммы Эйлера для трех взаимно пересекающихся множеств А, В, С (рис. 86).
A: k1=1
B: k2=1
C: k3=0
Рис. 86. Диаграмма Эйлера для кодирования по Хэммингу
четырехразрядной информации
Пусть произошла ошибка в разряде х2 (рис. 87).
Рис. 87. Ошибка в разряде х2
Искажение (ошибка) привела к изменению информации и нарушению нечетности в двух контрольных группах А и С. Именно это и укажет на номер искаженного разряда. Каждый сектор («кусочек») диаграммы Эйлера определяет один из разрядов n или k.
Для определения числа контрольного разряда необходимо использовать соотношение m£2k–1, или n+k£2k–1.
Далее строится матрица Хэмминга.
1 0 1 0 1 0 1
1 1 0 0 1 1 0
1 1 1 1 0 0 0
x4 x3 x2 k3 x1 k2 k1
Если дано число информационных разрядов n, то необходимо определить число контрольных разрядов. Выбираются двоичные эквиваленты номеров всех m разрядов (справа налево, младшие разряды вверху). Столбцы с одной единицей отводятся под контрольные разряды. Выделяются три группы контрольных разрядов k1, k2, k3.
В передатчике формируются контрольные разряды по нечётности k1,k2,k3 путём суммирования по модулю 2 соответствующих разрядов.
Записываются уравнения Хэмминга:
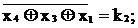
Уравнения синдрома ошибки включают и сами контрольные разряды, которые тоже могут исказиться.
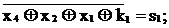
Синдром ошибки – вектор 
.
Если искажение не произошло, то синдром нулевой. Если не нулевой он укажет на место ошибки. Если (101), то ошибка в 5-ом столбце, разряд х2, поскольку этот разряд входит в две группы контроля по нечетности – первую и вторую – это области А и С диаграммы Эйлера (рис. 87).
Иногда реальную информацию передают в другом порядке: отдельно информационные, отдельно контрольные разряды. Представим информацию в матричном виде. Матрица Хэмминга обозначается Н. Информационную подматрицу обозначим Р, а контрольную – I:
Если 
– входной вектор, 
– полное кодовое слово, тогда кодирование заключается в следующих матричных операциях:
, где 
– конкатенация (сцепление) информации в определенном порядке следования разрядов.
На вектор 
воздействуют ошибки. Используем вектор ошибок 
:
,
где – вектор ошибки, указывающий, какие разряды исказились. Тогда получение синдрома ошибки выглядит так:
.
В матричных операциях используется сумма по модулю 2 (Å). Заметим, что описанный код Хэмминга, позволяет обнаруживать и исправлять только одиночные (однократные) ошибки. Для обнаружения двукратных ошибок вводят еще один контрольный разряд – для всей посылки.
