Наиболее часто используются базисы, состоящие из одной функции: И-НЕ, ИЛИ-НЕ.
Представление переключательной функции в этих базисах требует использования только этих операций с учетом ограничений по числу входов соответствующих элементов. Для этого используется закон Де Моргана:
f(аbсd)=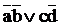 
= 
= 
– это представление в базисе И-НЕ.
– это представление в базисе ИЛИ-НЕ.
Соответствующие схемы представлены на рис. 63.
Рис. 63. Реализация логической функции f(аbсd)= 
в базисе 2И-НЕ (а) и 2ИЛИ-НЕ (б),
т.е. для двухвходовых элементов И-НЕ, ИЛИ-НЕ
В случае превышения ограничения по числу входов элементов следует еще раз применить закон Де Моргана, например:
т.е. получили только одноместные и двухместные операции И-НЕ.
Синтез в базисе Жегалкина.
Полиномом Жегалкина называется представление логической функции в базисе {Å,И,НЕ} (имеется соответствующая алгебра Жегалкина). В данном представлении инверсия реализуется как сумма по модулю 2 с константой 1.
Для представления ДНФ в виде полинома Жегалкина необходимо выразить дизъюнкцию через конъюнкцию и инверсию.
Например:
хÚy= 
=(хÅ1)(yÅ1)Å1=
=xyÅxÅyÅ1Å1=xyÅxÅy.
(1Å1=0).
Пример. Представить в виде полинома Жегалкина логическую функцию xÚyÚz.
xÚyÚz= 
=(хÅ1)(yÅ1)(zÅ1)Å1=(xyÅxÅyÅ1)(zÅ1)Å1=
=xyzÅxzÅyzÅxyÅxÅyÅ1Å1=xyzÅxzÅyzÅxyÅxÅy.
Для преобразования полинома Жегалкина используются обычные приемы элементарной алгебры (исключение составляет равносильность аÅа=0).
Полином Жегалкина может быть получен по таблице истинности путем суммирования по модулю 2 конъюнкций переменных без инверсии xi или инверсных переменных (xjÅ1) соответствующих рабочих наборов.
Например, получим полином Жегалкина для функции f, таблица истинности которой имеет вид табл. 54.
Таблица 54
Таблица истинности
| x | y | z | f |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Тогда получим:
f=(xÅ1)(yÅ1)zÅ(xÅ1)y(zÅ1)Åx(yÅ1)(zÅ1)Åxyz=
=(xyÅxÅyÅ1)zÅ(xzÅxÅzÅ1)yÅx(yzÅyÅzÅ1)Åxyz= 
=xÅyÅz,
что и требовалось доказать, ибо и рассматривалась функция сложения по модулю 2 трех аргументов.
Булева производная
Производная первого порядка 
от булевой функции f по переменной xi определяется следующим образом [9]:
=f(х1,х2,...,хi-1,1,xi+1,...,xn)Åf(x1,x2,...,xi-1,0,xi+1,...,xn),
где f(х1,х2,...,хi-1,1,xi+1,...,xn) – единичная остаточная функция, получаемая в результате подстановки вместо хi константы 1, а f(х1,х2,...,хi-1,0,xi+1,...,xn) – нулевая остаточная функция, получаемая в результате подстановки вместо xi константы 0.
Пример. f=х1Úх2.
Пример. 
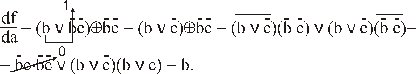
Пример.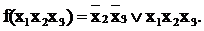 
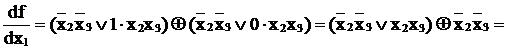
Булева производная по xi=0, если f не зависит от xi, булева производная по xi=1, если f зависит только от xi.
Булева производная первого порядка определяет условия, при которых функция изменяет свое значение при изменении значения переменной xi 
.
В нашем примере функция f(х1х2х3) изменяет свое значение при изменении х1, если истинна конъюнкция х2х3, т.е. х2=1, х3=1.
Пример. Определим все булевы производные функции 
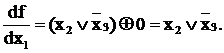
Итак, значение функции изменяется (функция переключается) при изменении х1, если х2=1 или х3=0 
; при изменении х2, если х1=х3=1 (х1х3=1); при изменении х3, если х1=1; х2=0 
.
Смешанная булева производная k-го порядка определяется путем вычисления k раз булевых производных первого порядка от булевых производных первого порядка, например [9]:
Булева производная k-го порядка равна сумме по модулю 2 всех производных первых, вторых, третьих,..., k-х смешанных производных, и определяет условия, при которых функция изменяет значение при одновременном изменении соответствующих переменных, например:
Таким образом, f переключается при одновременном переключении х1, х2, когда х3=0, либо независимо от х3 при переключении х1 и х2 с 1,1 на 0,0 или с 0,0 на 1,1.
При синтезе методом каскадов оптимальное исключение переменных достигается путем анализа веса производных [9]. Вес производной по данной переменной – число конституент соответствующей переключательной функции. То есть, сначала исключается переменная, производная которой имеет максимальный вес, что означает максимальное изменение функции при изменении переменной.
