Синтез комбинационных автоматов.
При синтезе комбинационных автоматов (после этапа абстрактного и структурного синтеза имеются соответствующие переключательные функции) требуется получить схему автомата, например, в виде переключательной схемы или схемы из функциональных (логических) элементов.
Синтез переключательной схемы.
Пусть задана переключательная функция 
Получим переключательную схему (рис. 57).
Рис. 57. Переключательная схема,
реализующая функцию 
На рис. 57 верхняя и нижняя горизонтальные линии обозначают, например, полюсы источника питания, а буква F – некоторый элемент, срабатывающий в случае равенства функции 
логический единице, т.е. в случае наличия цепи к верхнему полюсу. Символами переменных х1,х2,х3 могут обозначаться, например, контакты некоторых датчиков, а F – обмотка реле, контакт которого включает некоторый исполнительный орган (вентилятор, сирену, нагреватель и др. элементы автоматики). Соответствующая релейно-контактная схема изображена на рис. 58.
Часто датчики подключаются не непосредственно в цепи реализации переключательных функций, а через реле-повторители (рис. 59).
Рис. 58. Релейно-контактная схема
реализации логической функции
Рис. 59. Релейно-контактная схема реализации переключательной функции с реле-повторителями сигналов датчиков
Синтез комбинационных автоматов на основе функциональных (логических) элементов по сравнению с переключательными схемами требует особого представления логической функции – в виде суперпозиции операций заданного базиса.
Синтез в базисе И, ИЛИ, НЕ.
Наиболее просто это сделать, если задать базис И, ИЛИ, НЕ. Предполагается, что переключательная функция представлена в ДНФ.
Пусть, например, задана следующая переключательная функция: z(аbсdx2x1)= 
Получим схему в базисе И, ИЛИ, НЕ (рис. 60).
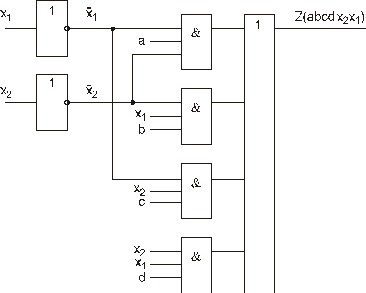
Рис. 60. Схема в базисе И, ИЛИ, НЕ без ограничения числа входов
функциональных элементов
Схема рис. 60 изображена в предположении, что число входов элементов не ограничено.
Если же должны использоваться только двухвходовые элементы, т.е. все операции бинарные (кроме инверсии), то схема будет выглядеть так, как изображено на рис. 61.
Рис. 61. Схема с учетом наличия только двухвходовых элементов И, ИЛИ
Синтез методом каскадов.
При синтезе комбинационных автоматов используется метод каскадов, основанный на разложении Шеннона:
f(x1,...,xi,...,xn)=xif(x1,...,1,...,xn)Ú 
if(x1,...,0,...,xn)=xif(1)Ú if(0).
Такое разложение позволяет исключать переменные и понижать размерность по каскадам до тех пор, пока остаточные функции не будут иметь простой вид и их реализация не будет представлять трудности [9].
Реализуем вышерассмотренную функцию z(аbсdx2x1) методом каскадов с использованием блоков исключения переменной вида xif(1)Ú if(0), которые легко реализуются в базисе И, ИЛИ, НЕ.
Очевидно, что:
z(аbсdx2x1)= 
,
т.е.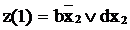 
, 
, которые реализуются на двухвходовых элементах И, ИЛИ. Проводить дальнейшее разложение нет необходимости. Соответствующая схема комбинационного автомата изображена на рис. 62.
Рис. 62. Схема, построенная по методу каскадов
Интересно, что схема на рис. 62, построенная по методу каскадов, проще в смысле числа элементов – для ее построения необходимо 11 элементов (9 двухвходовых и 2 инвертора). Сравните ее со схемой на рис. 61, для построения которой потребовалось 13 элементов (11 двухвходовых и 2 инвертора).
В общем случае сложность остаточных функций зависит от порядка исключения переменных и оптимальное их исключение ищут специальными методами, основанными на понятии булевой производной:
=f(x1,x2,...,xi-1,1,xi+1,...,xn)Åf(x1,x2,...,xi-1,0,xi+1,...,xn),
где Å – сумма по модулю 2 [9].
При использовании базисов, отличных от рассмотренного базиса И, ИЛИ, НЕ, блоки исключения переменных и блоки реализации остаточных функций реализуются в заданном базисе.
Например, в импликативном базисе {®,0}:
=(а®(b®0))®0.
