Алгебраические системы. Решетки

 

Выше рассматривались алгебры, т.е. множества, на которых заданы операции [19].

Множества, на которых кроме операций заданы отношения, называются алгебраическими системами [19]. Таким образом, алгебры можно считать частным случаем алгебраических систем. Другим частным случаем алгебраических систем являются модели – множества, на которых заданы только отношения.

Рассмотрим пример алгебраической системы, который наиболее часто встречается в теоретической алгебре и ее применениях [19]. Этот пример – решетка.

Рассмотрим алгебраическую систему из множества М, отношения порядка (будем обозначать £) и некоторых операций. Говорят, что множество М линейно упорядочено, если любые два элемента находятся в отношении упорядоченности, иначе – частично упорядочено. Для элементов а и b из М их верхней гранью (мажорантой) называется любой элемент сÎМ такой, что с³а, с³b, а их нижней гранью (минорантой) – любой элемент dÎМ такой, что d£а, d£b. В общем случае для некоторых элементов а и b верхняя или нижняя грань может не существовать или быть не единственной, причем различные верхние (или нижние) грани могут быть несравнимыми. Во множестве верхних и нижних границ вводится понятие точной верхней (нижней) границы множества.

Такая верхняя граница множества обозначается supМ («супремум»), такая нижняя граница – обозначается infМ («инфинум»).

Частично упорядоченное множество называется решеткой, если у каждой пары его элементов а,b необходимо имеются единственная точная верхняя граница sup(а,b) или пересечение аÙb и точная нижняя граница inf(а,b) или объединение аÚb. Здесь операции Ù,Ú пока понимаются как абстрактные операции алгебраической системы и отличаются от теоретико-множественных операций объединения и пересечения. Для алгебры множеств Ù соответствует I, Ú соответствует U.

Рассмотрим пример частично упорядоченного множества – диаграмму (решетку) Хассе [9], известную с конца XIX века и применяемую в генеалогии для задания родства (рис. 8).

 

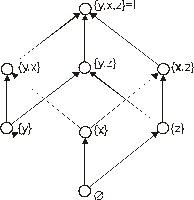
Рис. 8. Диаграмма (решетка) Хассэ для множества всех

подмножеств универсального множества I={y,x,z}

 

На рис. 8 множество всех подмножеств данного множества упорядочено по отношению включения, а операции объединения и пересечения элементов связаны дистрибутивными законами. Нулем и единицей частично упорядоченного множества называются, соответственно, его наименьший и наибольший элементы, обычно применяются традиционные обозначения 0,1.

Так, на рис. 8 нулем и единицей будут, соответственно, пустое множество Æ и данное множество (I).

На решетке Хассе обычно не изображаются линии транзитивности и рефлексивности.

В частично упорядоченных множествах с нулем и единицей, вводится операция дополнения элементов.

Элементы а и в частично упорядоченного множества с нулем 0 и единицей 1 называются дополнительными друг для друга, если их пересечение равно нулевому элементу 0, а объединение дает единичный элемент 1: аÙb=0, аÚb=1.

Так, {y}I{x,z}=Æ, {y}U{x,z}=I на рис. 8.

Дистрибутивная решетка с отличными друг от друга нулем и единицей, в которой каждый элемент имеет дополнение, называется булевой алгеброй.

Пример булевой алгебры – совокупность множества всех подмножеств данного множества и теоретико-множественных операций объединения, пересечения и дополнения, т.е. алгебра Кантора (алгебра множеств), рассмотренная выше. Операции объединения и пересечения являются бинарными (двухместными), а операция дополнения – унарной (одноместной).

Далее мы рассмотрим другой пример булевой алгебры – булеву алгебру логических (переключательных) функций.

 

Задание множеств конституентами

Формула алгебры множеств, представляющая собой пересечение, в которое входят по одному разу все множества (со знаками дополнения или без дополнений) на данном универсуме, называется конституентой единицы [9]. Формула, представляющая собой объединение, в которое входят по одному разу все множества (со знаками дополнения или без дополнений) на данном универсуме, называется конституентой нуля. Каждое множество, за исключением пустого, может быть задано объединением конституент единицы. Каждое множество за исключением универсального может быть задано пересечением конституент нуля. Рассмотрим задание множества путем указания его конституент единицы. Пусть на некотором универсуме рассматриваются два взаимно пересекающихся множества: А и В.

Зададим их графически с помощью диаграмм Эйлера (рис. 9).

 

 

Рис. 9. Диаграмма Эйлера для двух взаимно пересекающихся

множеств А и В на универсуме I

 

Тогда каждый из четырех сегментов (четырех «кусочков») этой диаграммы может быть закодирован конституентой, содержащей символы А и В:

 – сегмент 00 – не А и не В;

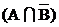 – сегмент 10 – А, но не В;

 – сегмент 01 – не А и В;

 – сегмент 11 – А и В.

В таком случае, заданное множество можно закодировать двоичным кодом в соответствии с тем, входят ли в него указанные конституенты (табл. 4):

                                                                                           Таблица 4

Задание множества А двоичным числом

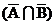
11	10	01	00
23	22	21	20
1	1	0	0

 

Множество А закодировано двоичным числом 1100. Этому двоичному числу соответствует десятичное число 12.

При таком задании множеств легко выполняются операции над ними. Например, получим пересечение множества №12 и множества №5. Результатом будет множество №4. Действительно, результат пересечения – множество, в котором при его двоичном представлении, имеются единицы в разрядах, соответствующих совпадениям единиц в исходных множествах (табл. 5).

Таблица 5

Пересечение множеств №12 и №5

1	1	0	0	№12
0	1	0	1	№5
0	1	0	0	№4=(№12)I(№5)