В языке Паскаль множеством называется конечный неупорядоченный набор элементов [2]. Все элементы одного множества должны принадлежать к одному и тому же типу, который называется базовым типом данного множества. В качестве базового типа можно использовать любой простой тип, кроме вещественного. Множество должно быть описано в разделе описания типов. Общий вид описания:
Type имя=set of базовый_тип;
Пример.
Пусть в нашем распоряжении имеется множество монет различного достоинства: 1р, 5р и 10р. Из этих монет можно составить следующее подмножества (их число равно 23=8):
1р; 5р; 10р; 1р, 5р; 1р, 10р; 5р, 10р; 1р, 5р, 10р; пустое множество.
Эти подмножества и будут принадлежать некоторому множеству sum. Сами элементы (монеты), из которых состоит подмножество, пусть принадлежат некоторому базовому типу monet. Тогда описание будет иметь вид:
Type monet=(r1,r5,r10);
Var sum:set of monet;
В программе значение переменной типа «множество» изображается путем перечисления конкретных компонентов подмножества, разделенных запятыми и заключенных в скобки [ ]. Такие изображения называются конструкторами множеств. Например: [r1], [r1,r10].
С переменной типа set допустимы следующие операции: =, <>, >=, <=, In, +, –, *,:=.
Пример использования операции присваивания:
Type n=1..9;
Var k:set of n;
........
k:=[3..6];
В этом случае в ячейку k будет записана комбинация [3,4,5,6].
Операции = и <> используются для проверки эквивалентности: два значения переменной типа set считаются равными, если они состоят из одних и тех же элементов.
Пример.
[1,3]=[3,1] – дает True;
[1..3]=[1,2,3] – дает True;
[1]<>[2] – дает True;
[1,2,3]=[1,4,3] – дает False.
Операции >= и <= используются для проверки принадлежности одного множества другому: так, если множество а содержится в множестве b, то а<=b дает True. Например: [1,2]<=[1,2,3] дает True.
Операция In используется для установления наличия определенного элемента в множестве. Так, если x есть элемент множества b, то (x In b) дает True.
Пример: [3] In [1,2,3] дает True.
Если a и b – операнды, имеющие один и тот же конкретный тип, то к ним применимы операции:
+ объединение;
– дополнение;
* пересечение.
Так, a+b представляет собой объединение множества элементов, входящих в a или в b (одинаковые элементы не повторяются); a–b – это множество элементов, которые есть в a, но отсутствуют в b; a*b представляет собой объединение множества элементов, входящих в множества a и b одновременно.
Пример.
[1,3]+[1,4] – дает [1,3,4];
[1,3]–[1,4] – дает [3];
[1,3]*[1,4] – дает [1].
Операция a:=a+x добавляет элемент x к множеству a, а операция a:=a–x исключает x из a.
Рассмотрим несколько примеров решения задач на Паскале, использующих множества [3].
З а д а ч а 1. Задать множество целых чисел от заданного числа до числа в три раза большего, чем заданное.
Решение. Используем описание множеств на языке Паскаль и операторы для работы с множествами.
Если количество элементов n в множестве известно заранее, то задача решается так:
const n=50;
type setnum=set of byte;
const mn:setnum=[n..3*n];
{В тексте программы остается использовать созданное множество}.
Если начальное значение задается пользователем, то задача решается так:
type setnum=set of byte;
var mn:setnum;
n,i:byte;
begin write('задайте первый элемент множества ');
readln(n);
if 3*n<256 then for i:=n to 3*n do mn:=mn+[i]
else write('заданное количество элементов не поместится в множестве ');
end.
З а д а ч а 2. Вывести на экран элементы множества, содержащего прописные и строчные буквы латинского алфавита.
Решение. В цикле проверим вхождение всех элементов базового типа и выведем те, которые входят в множество.
var zn:set of 'A'..'z';
i:char;
begin for i:='A' to 'Z' do
if i in zn then write(i,' ');
for i:='a' to 'z' do
if i in zn then write(i,' ');
end.
З а д а ч а 3. Написать программу, которая в заданном слове, состоящем из строчных букв, определяет составляющие его буквы, глухие и звонкие согласные, затем все согласные и все гласные буквы.
Решение.
type setchar=set of char;
const GL:setchar=['п','ф','к','т','ш','с','х','ц','ч',
'щ']; {множество глухих согласных}
ZV:setchar=['л','м','н','р','й','б','в','г','д','ж',
'з']; {множество звонких согласных}
ALF:string='абвгдеёжзийклмнопрстуфхцчшщъыьэюя';
{строка – русский алфавит}
var s:string; {заданное русское слово}
i:integer; {номер обрабатываемого символа в слове}
mgl:setchar; {множество глухих согласных}
mzv:setchar; {множество звонких согласных}
buk:setchar; {множество всех букв слова}
sog:setchar; {множество согласных слова}
gla:setchar; {множество гласных слова}
procedure print(s:string;mn:setchar);
{процедура вывода элементов множества с предшествующим комментарием}
var i:integer;
begin write(s,' ');
for i:=1 to length(ALF) do
if ALF[i] in mn then write(ALF[i],' ');
writeln;
end;
begin write('Введите русское слово ');
readln(s);
mgl:=[]; mzv:=[]; buk:=[];
{вначале множества букв пусты}
for i:=1 to length(s) do
begin buk:=buk+[s[i]]; {объединили букву с множеством букв}
if s[i] in GL
then mgl:=mgl+[s[i]]
{объединили глухую согласную с множеством глухих согласных}
else if s[i] in ZV
then mzv:=mzv+[s[i]];
{объединили звонкую согласную с множеством
звонких согласных}
end;
{находим множество согласных букв}
sog:=mgl+mzv;
{находим множество гласных букв}
gla:=buk-(sog+['ь','ъ']);
print('слово состоит из букв; ',buk);
print('гласные буквы: ',gla);
print('согласные буквы: ',sog);
print('глухие согласные: ',mgl);
print('звонкие согласные; ',mzv);
end.
З а д а ч а 4. Написать программу для нахождения простых чисел с помощью «решета Эратосфена».
Решение.
1. Поместим все числа между 2 и n (n<=255) в решето.
2. Выберем из решета наименьшее из чисел.
3. Поместим это число среди простых.
4. Переберем и вынем из решета все числа, кратные данному.
5. Если решето не пустое, то повторим шаги 2–5.
const n=255; {количество элементов в множестве}
var interval, {решето}
prost:set of 2..n; {множество простых чисел}
next:integer; {наименьшее число в решете}
c:integer; {новое простое число}
j:integer; {переменная для удаления из решета чисел,кратных текущему простому числу}
begin interval:=[2..n];
prost:= [];
next:= 2;
repeat {поиск очередного простого числа}
while not (next in interval) do next:=succ(next);
prost:=prost+[next];
c:=2*next–1;
j:=next;
while j<=n do
begin interval:=interval–[j]; j:=j=c; end;
until interval=[];
end.
ЭЛЕМЕНТЫ ОБЩЕЙ АЛГЕБРЫ
Операции на множествах
Частным случаем функции является операция, т.е. функциональное отображение вида j: MnaМ, где a знак отображения. Такая функция называется n-арной операцией, в ней области определения аргументов и область значений функции совпадают, n-местная операция по n элементам множества определяет (n+1)-й элемент этого же множества [9-10].
Алгеброй А называется совокупность <> множества М с заданными на нем операциями S={j11,j12,...j1n1,j21,...j2n2,jm1,jm2,...jmnm}, А=<М,S>, где множество М – носитель, S – сигнатура алгебры [9-10, 19]. Каждый первый индекс у идентификатора операции указывает ее местность.
Алгебра типа <М,j2>, т.е. алгебра с бинарной операцией, называется группоидом.
Рассмотрим квадрат с вершинами в точках а1, а2, а3, а4, пронумерованных против часовой стрелки, и повороты квадрата вокруг центра также против часовой стрелки, переводящие вершины в другие вершины [19]. Таких поворотов бесконечное множество: на углы 0,  , p, 3
, p, 3  , 2p, 5
, 2p, 5  ,..., однако они задают всего четыре различных отображения множества вершин в себя, соответствующих первым четырем поворотам.
,..., однако они задают всего четыре различных отображения множества вершин в себя, соответствующих первым четырем поворотам.
Можно сказать, что задана алгебра А=<М,j1> с основным множеством М={а1,а2,а3,а4} и четырьмя унарными операциями МaМ, которые обозначим буквами a, b, n, d. Зададим эти операции таблицей (табл. 1).
Таблица 1
Унарные операции алгебры поворотов квадрата
| a | b | n | d | |
| а1 | а1 | а2 | а3 | а4 |
| а2 | а2 | а3 | а4 | а1 |
| а3 | а3 | а4 | а1 | а2 |
| а4 | а4 | а1 | а2 | а3 |
| 0 | 
| p | 3 
|
Можно интерпретировать такие операции также циклическими сдвигами бит информации вида:
 .
.
Множество 0={a,b,n,d} отображений вершин в себя вместе с бинарной операцией 02a0 последовательного выполнения отображений (выполнения поворота за поворотом, композиции поворотов), которую обозначим символом «¤» образует алгебру с бинарной операцией <0, ¤> [19]. Она задается табл. 2, в которой на пересечении строки i и столбца j записан результат операции ioj.
Таблица 2
Бинарные операции 02a0 алгебры
композиций поворотов квадрата
 i
j i
j
| a | b | n | d | |
| a | a | b | n | d | |
| b | b | n | d | a | |
| n | n | d | a | b | |
| d | d | a | b | n | i¤j |
Такая таблица (см. табл. 2), задающая бинарную операцию, называется таблицей Кэли.
Можно представить бинарной операцией, например, смешивание красок, когда из двух цветов получается третий, входящий, однако во множество всех цветов.
Пусть А=<М,j2> – группоид. Обозначим, как и в предыдущем примере, j2 символом ¤ [9].
Тогда элемент nÎМ называется правым нейтральным элементом группоида А, если для всякого mÎМ выполняется равенство m¤n=m.
Для левого нейтрального элемента выполняется равенство n¤m=m.
В дальнейшем для краткости вместо слов «все», «всякий» будем использовать символ " (перевернутая буква А – первая буква английского слова All – все, этот символ называется еще квантором общности; квантор существования обозначается $ и означает «существует», «имеется», «есть»).
Элемент n, являющийся одновременно и левым, и правым нейтральным элементом, называют двухсторонним нейтральным элементом или просто нейтральным элементом.
Для смешивания красок нейтральный элемент – бесцветный лак.
Если группоид <М, ¤> мультипликативный, т.е. его бинарная операция ¤ имеет тип умножения (·), то нейтральный элемент называется единицей и обозначается 1, если группоид аддитивный, т.е. бинарная операция ¤ имеет тип сложения (+), то нейтральный элемент называется нулем и обозначается 0 [9]. Нейтральный элемент в группоиде всегда единственный.
Коммутативный группоид, т.е. группоид, в котором
("х,yÎМ)(х¤y=y¤х),
называется коммутативным или абелевым.
Группоид, в котором выполняется закон ассоциативности
("х,y,zÎМ)(х¤ (y¤z)=(x¤y) ¤z),
называется ассоциативным или полугруппой.
Полугруппа с единицей называется моноидом. В алгебре поворотов квадрата (см. табл. 2) единицей служит поворот на нулевой угол (a).
Группой называется полугруппа с единицей, в которой для каждого элемента а существует элемент а-1, называемый обратным (а¤а-1=а-1¤а=n) и каждое из уравнений a¤x=b, y¤a=b обладает единственным решением [9].
В алгебре поворотов квадрата (см. табл. 2), являющейся группой, обратным к данному повороту является поворот, дополняющий его до 2p:
b-1=d, n-1=n, d-1=b.
Группа, все элементы которой являются степенями одного элемента а, называется циклической. Циклическая группа всегда абелева.
Множество рациональных чисел, не содержащее нуля, с операцией умножения является абелевой группой. Обратным к элементу а, является элемент  .
.
Группа подстановок Галуа
Рассмотрим знаменитую группу подстановок, которую исследовал выдающийся французский математик Э. Галуа (1811-1832 гг.) [9].
Обладая феноменальными математическими способностями, он настолько опередил современников в своих теоретических исследованиях, что при жизни так и не был понят даже великими Фурье и Пуассоном, и даже не был принят в Политехническую школу – центр математической мысли Франции тех лет. «Неистовый республиканец», «любимец богов» был отважным революционером, сидел в тюрьме за участие в антиправительственных выступлениях и погиб на дуэли в возрасте 20 лет. Основную часть своих результатов согласно легенде он записал ночью перед дуэлью, а признан был только спустя много лет после смерти. Хотя его труды составляют всего около 60 страниц, многое в них еще до сих пор не понято математиками и ждет своего разрешения.
Подстановкой n-ой степени называется взаимно однозначное отображение множества из n элементов в себя.
Рассмотрим всего три элемента: х1, х2, х3.
Существует шесть вариантов последовательностей из трех элементов:
х1х2х3, х2х3х1, х1х3х2, х3х1х2, х2х1х3, х3х2х1.
Запишем порождение этих вариантов следующим образом:

Эта запись означает, что х1 переходит (отображается) в х2, х2 – в х3, х3 – в х1.
Число таких возможных подстановок равно числу вариантов последовательностей из трех элементов. Обозначим возможные подстановки:
 ,
,  ,
,  ,
,
 ,
,  ,
, 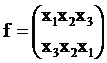 .
.
Произведением подстановок назовем последовательное выполнение сначала первой, а затем второй из перемножаемых подстановок.
Например,

Таким образом, имеем алгебру <П,¤>, где П – множество подстановок {а,b,с,d,e,f}, ¤ – бинарная операция П2aП.
Соответствующая таблица Кэли для алгебры постановок Галуа имеет вид табл. 3.
Таблица 3
Таблица Кэли для алгебры подстановок Галуа
 j
i j
i
| а | b | с | d | e | f | |
| a | a | b | с | d | e | f | |
| b | b | а | d | с | f | е | |
| с | с | е | а | f | b | d | |
| d | d | f | b | е | а | с | |
| е | е | с | f | а | d | b | |
| f | f | d | е | b | с | а | i¤j |
В такой алгебре выполняется закон ассоциативности, но не выполняется закон коммутативности.
Нейтральным элементом является подстановка а.
Группа – это полугруппа взаимно однозначных преобразований, причем именно однозначность гарантирует наличие обратного преобразования. Можно сказать, что в группе при любом числе умножений не теряется информация об исходном элементе: если известно, на что умножали, всегда можно узнать что умножали. Для полугруппы это верно не всегда. Пусть дана дискретная система с конечным числом состояний S={S1,...,Sn}, на вход которой может быть подано входное воздействие из множества x={x1,...,xm}. Всякое входное воздействие однозначно переводит состояние системы в некоторое другое состояние, т.е. является преобразованием множества S. Последовательности воздействий – композиция преобразований, поэтому множество всех последовательностей – полугруппа с образующими {x1,...,xm}. Если такая полугруппа является группой, то по любой входной последовательности и заключительному состоянию системы можно однозначно определить ее начальное состояние [19].
Алгебра <М,·,+>, которая по умножению (·) является мультипликативным группоидом, а по сложению (+) – абелевой группой, причем умножение связано со сложением законом дистрибутивности
а·(b+с)=а·b+а·с
(b+с)·а=b·а+с·а,
называется кольцом. Например, числовыми кольцами являются множество целых чисел Z, множество рациональных чисел R, множество действительных чисел D, множество комплексных чисел К.
Кольцо, в котором все отличные от нуля элементы составляют группу по умножению, называется телом (имеются обратные элементы по умножению). Тело, у которого мультипликативная группа абелева, называется полем. Таковы поля Галуа.






